На малюнку показано зміну температури повітря протягом трьох діб. По горизонталі вказується дата і час, по вертикалі — значення температури в градусах Цельсія. Визначте на малюнку різницю між найбільшою та найменшою температурою повітря 15 липня. Відповідь дайте у градусах Цельсія.
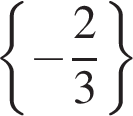
Цукерки, що лежать у коробці, можна порівну поділити між двома або трьома дітьми, але не можна поділити порівну між чотирма дітьми. Якому з наведених значень може дорівнювати кількість цукерок у цій коробці?
Дано дві правильні чотирикутні піраміди. Обсяг першої піраміди дорівнює 16. У другої піраміди висота в 2 рази більша, а сторона основи в 1,5 рази більша, ніж у першої. Знайдіть обсяг другої піраміди.
Розв'яжiтъ рiвняння 
На малюнку зображено трикутник АВС , в якому
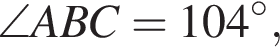
 Використовуючи дані малюнка, знайдіть градусну міру кута ANM чотирикутника ABMN .
Використовуючи дані малюнка, знайдіть градусну міру кута ANM чотирикутника ABMN .
На рисунку зображено графік функції
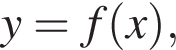 визначеної на проміжку [—3; 3]. Одна з наведених точок, абсциса якої є від’ємним числом, а ордината — додатним, належить цьому графіку. Укажіть цю точку.
визначеної на проміжку [—3; 3]. Одна з наведених точок, абсциса якої є від’ємним числом, а ордината — додатним, належить цьому графіку. Укажіть цю точку.
Спростіть вираз 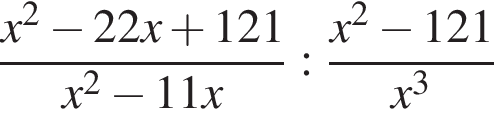 .
.
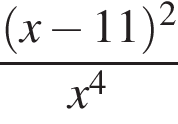
Площу будь-якого опуклого чотирикутника можна обчислювати за формулою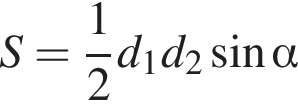 , де
, де![]() - Довжини його діагоналей, а
- Довжини його діагоналей, а![]() кут між ними. Обчисліть
кут між ними. Обчисліть![]() , якщо
, якщо .
.
Результат розкладання многочлена x (6 a − b ) + b − 6 a на множники має вигляд:
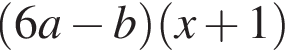
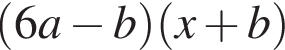
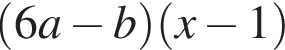
Яке з наступних тверджень є вірним?
I. Усі кути ромба рівні.
ІІ. Якщо сторони одного чотирикутника відповідно дорівнюють сторонам іншого чотирикутника, то такі чотирикутники рівні.
ІІІ. Через будь-яку точку, що лежить поза колом, можна провести дві дотичні до цього кола.
Розв'яжіть рівняння 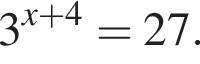
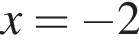
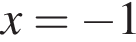
Обчислігь плошу зафарбованої фігури, зображеної на рисунку.
Укажiть число, що є розв'язком нерiвностi 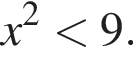
Знайдіть значення виразу
Площа бічної поверхні п’ятикутної піраміди дорівнює 13. Чому дорівнює площа бічної поверхні піраміди, якщо всі її ребра зменшити в 2 рази?
На рисунку зображено фрагмент поперечного перерiзу стiни (прямокутник KLMN) з арковим прорiзом ABFCD, верхня частина BFC якого є дугою кола радiуса 1 м. Вiдрiзки AB i DC перпендикулярнi до AD, AB = DC = 2 м. AD = 1,6 м, KL = 2,75 м. Визначте вiдстань d вiв найвищої точки F прорiзу до стелi LM.
На рисунках (1−4) зображено графіки функцій, визначених на відрізку [−4; 4].
До кожного п очатку речення (1−4) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Функція, графік якої зображ ено на рис. 1,
2. Функція, графік якої зображ ено на рис. 2,
3. Функція, графік якої зображ ено на рис. 3,
4. Функція, графік якої зображ ено на рис. 4,
А рис. є непарною.
Б рис. набуває найбільшого значення, що дорівнює 4.
В рис. є парною.
Г рис. має три нулі.
Д рис. має дві точки локального екстремуму.
Нехай m і n — довільні дійсні числа, a — довільне додатне число, ![]() До кожного початку речення (1−4) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
До кожного початку речення (1−4) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Якщо 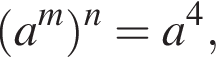 то
то
2. Якщо 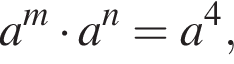 то
то
3. Якщо  то
то
4. Якщо 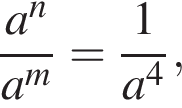 то
то
А 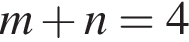
Б 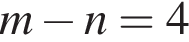
В 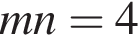
Г 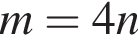
Д 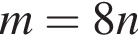
На кожному з рисунків зображено коло з центром у точці О та хорду АВ. Кут ACB і ADB — вписані кути, які спираються на хорду АВ. Установіть відповідність між вписаним кутом АСВ, зображеним на рисунках (1−4), та його градусною мірою (А−Д).
А 100°
Б 90°
В 80°
Г 60°
Д 50°
У циліндр з радіусом основи 3 см і висотою 4 см вписано конус (див. рисунок). До кожного початку речення (1−4) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Площа бічної поверхні циліндра дорівнює
2. Площа повної поверхні циліндра дорівнює
3. Площа основи конуса дорівнює
4. Площа бічної поверхні конуса дорівнює
А 9π см2
Б 12π см2
В 15π см2
Г 24π см2
Д 42π см2
Перший автомат за 2 хвилини наповнює гелієм 3 однакові повітряні кульки, а другий автомат за цей самий час — на 100% ільше таких кульок. Уважайте, шо продуктивність роботи автоматів є сталою.
1. За скільки секунд другий автомат наповнює гілієм одну повітряну кульку?
2. Скільки всього повітряних кульок наповнять гелієм обидва автомати за 10 хвилин одночасно?
У прямокутній трапеції АВСО проведено середню лінію MN (див. рисунок). Даний  см,
см,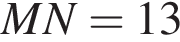 см
см
1. Визначте довжину сторони AD (у см).
2. Визначте довжину сторони AB (у см).
У прямокутній системі координат у просторі задано вектор 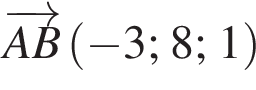 і точку
і точку 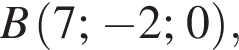 точка О — початок координат.
точка О — початок координат.
1. Визначте ординату y точки 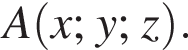
2. Обчисліть скалярний добуток 
Другий член арифметичної прогресії (an) на 7,2 більший за її шостий член.
1. Визначте різницю d цієї прогресії.
2. Визначте перший член a1 цiєї прогресії, якщо 
Маша колекціонує принцес із Кіндер-сюрпризів. Всього в колекції 10 різних принцес і вони рівномірно розподілені, тобто в кожному черговому Кіндер-сюрпризі може з рівними ймовірностями виявитися будь-яка з 10 принцес. Маша вже має дві різні принцеси з колекції. Яка ймовірність того, що для отримання наступної принцеси Маші доведеться купити ще 2 або 3 шоколадні яйця?
Залізничний потяг довжиною в 1 км пройшов би повз стовп за 1 хв., а через тунель (від входу локомотива до виходу останнього вагона) за тієї ж швидкості — за 3 хв. Яка довжина тунелю (км)?
Спростіть вираз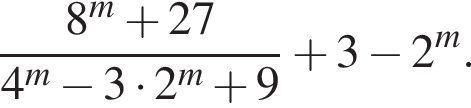
Розв'яжіть рівняння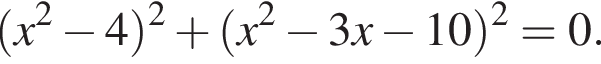 У відповіді напишіть суму всіх його дійсних коренів.
У відповіді напишіть суму всіх його дійсних коренів.
Марійка зірвала на клумбі 9 нарцисів та 4 тюльпани. Скільки всього існує способів вибору із цих квітів 3 нарцисів та 2 тюльпанів для букета?
Задано функцію 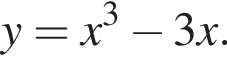
| x | y |
|---|---|
| 0 | |
| −1 | |
| 2 |
1. Для наведених у таблиці значень аргументи х визначте відповідні їм значення у (див. таблиця).
2. Визначте й запишіть координати точок перетину графіка функції 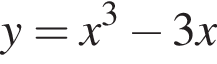 із віссю x.
із віссю x.
3. Знайдіть похідну f' функції 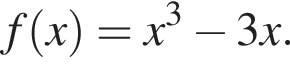
4. Визначте нулі функції f'.
5. Визначте проміжки зростання і спадання, точки екстремуму й екстремуми функції f.
6. Побудуйте ескіз графіка функції f.
Бічні ребра правильної трикутної піраміди дорівнюють 7. Плоский кут при вершині дорівнює γ.
1. Зобразіть на малюнку цю піраміду та кут γ.
2. Знайдіть апофему.
3. Знайдіть площу повної поверхні піраміди.
Відповідно до умови завдання 31 (№ 3514) сторона основи правильної чотирикутної піраміди дорівнює 3. Бічні ребра нахилені до основи під кутом α.
1. Зобразіть на малюнку цю піраміду та побудуйте лінійний кут двогранного кута при бічному ребрі.
2. Знайдіть цей кут.
Доведіть тотожність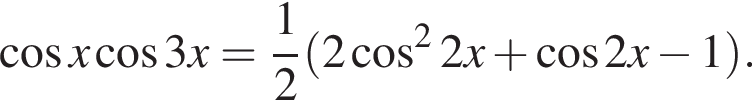
Задано нерівність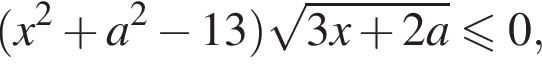 де x – змінна, a – параметр.
де x – змінна, a – параметр.
1. Розв'яжіть нерівність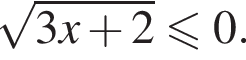
2. Знайдіть усі значення параметра a , при кожному з яких нерівність має не більше двох розв'язків.

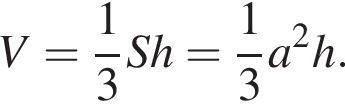 Следовательно, отношение объёмов пирамид:
Следовательно, отношение объёмов пирамид: 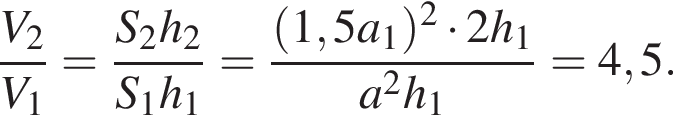
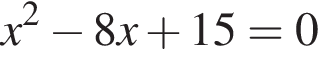 по теореме Виета сумма корней 8, а произведение 15. Подходят тогда числа 3 и 5. Они действительно корни по обратной теореме Виета.
по теореме Виета сумма корней 8, а произведение 15. Подходят тогда числа 3 и 5. Они действительно корни по обратной теореме Виета. Так как сумма углов треугольника равна 180°,
Так как сумма углов треугольника равна 180°, 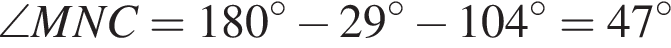 . Угол ANM вертикальный с найденным. Значит, он равен
. Угол ANM вертикальный с найденным. Значит, он равен 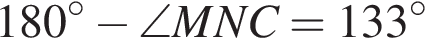 .
.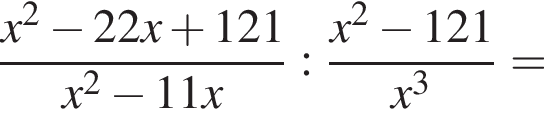
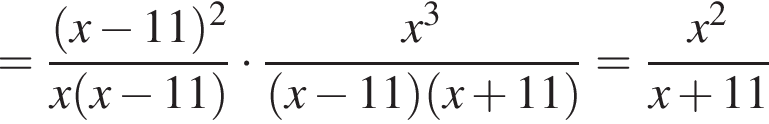
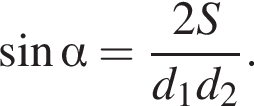
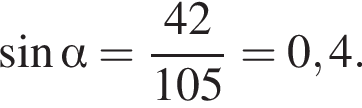

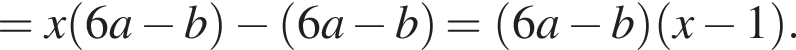

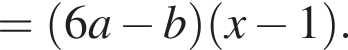
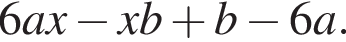
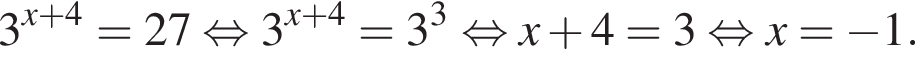
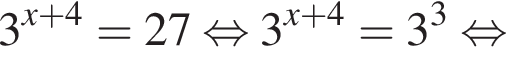
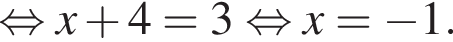
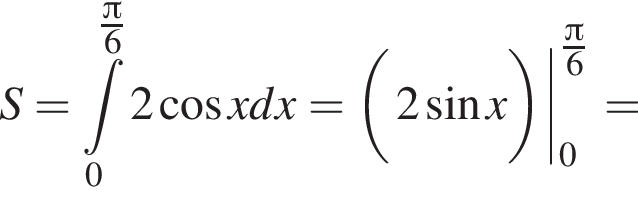
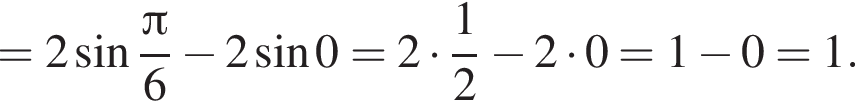
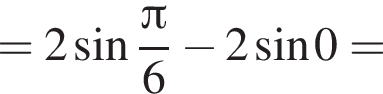
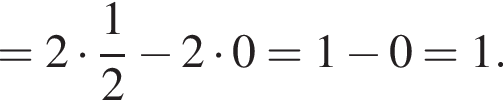
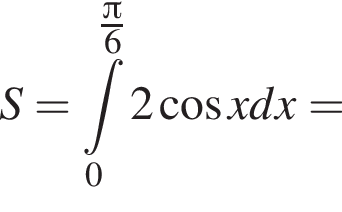
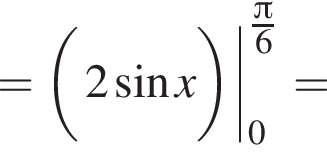
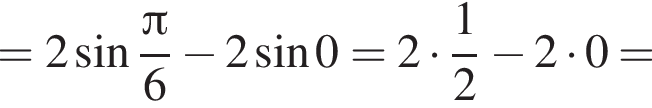
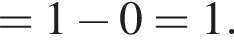
 Если подставить в неравенство остальные числа — они не подойдут.
Если подставить в неравенство остальные числа — они не подойдут.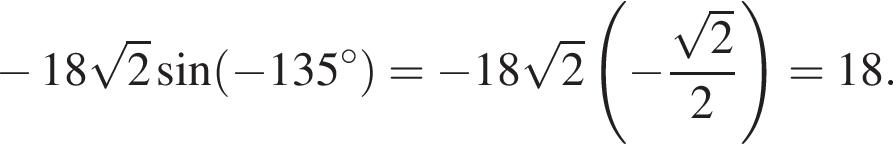
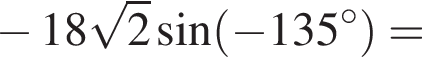
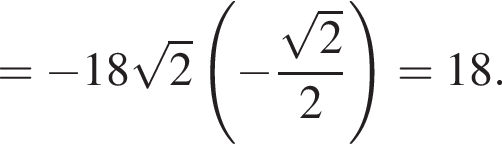
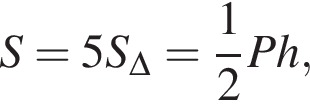
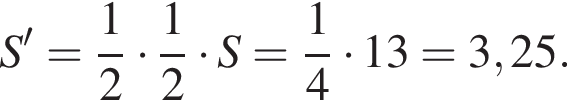
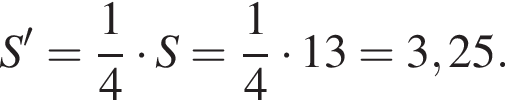
 м
м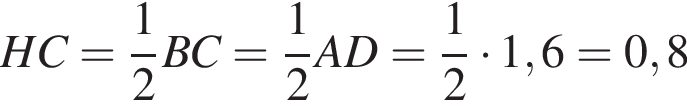 м
м

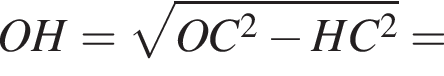
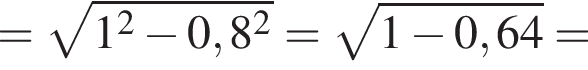
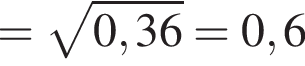
 м
м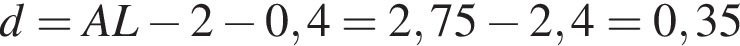 м.
м.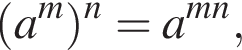 поэтому если
поэтому если 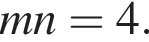
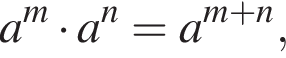 поэтому если
поэтому если 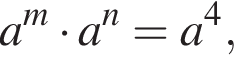 то
то 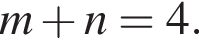
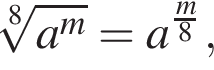
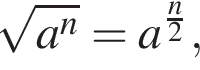 поэтому если
поэтому если  то
то 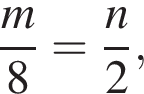 откуда
откуда 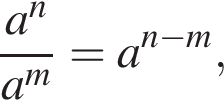 поэтому если
поэтому если 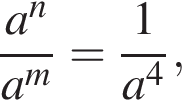 то
то 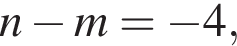
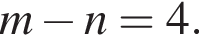
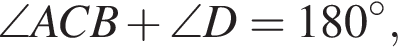 определим, что
определим, что  Итак, 1 — В.
Итак, 1 — В. 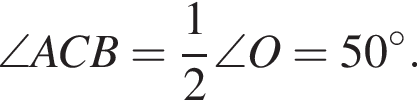 Таким образом, 2 — Д.
Таким образом, 2 — Д. 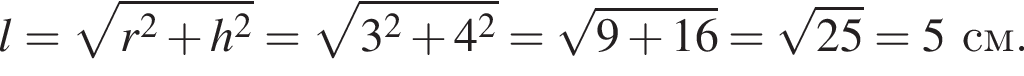
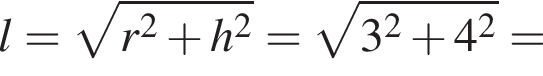

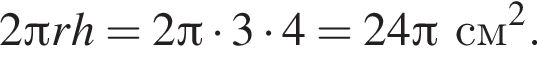 Площадь полной поверхности цилиндра тогда равна
Площадь полной поверхности цилиндра тогда равна 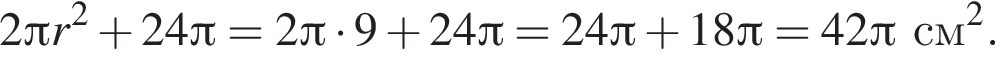
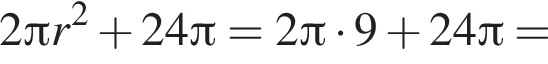
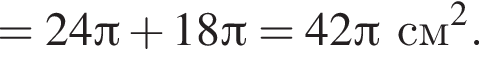
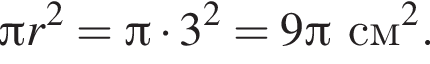 Площадь боковой поверхности конуса равна
Площадь боковой поверхности конуса равна 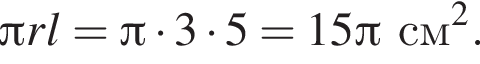
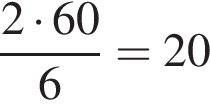 секунд. Оба автомата вместе за 2 минуты наполнят
секунд. Оба автомата вместе за 2 минуты наполнят 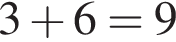 шариков, а за 10 минут — в
шариков, а за 10 минут — в 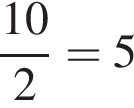 раз больше, то есть 45 шариков.
раз больше, то есть 45 шариков.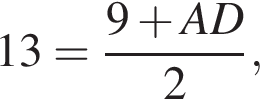 откуда
откуда 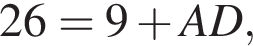
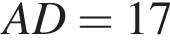 см. Опустим перпендикуляр CH на сторону AD. Тогда треугольник CHD — прямоугольный равнобедренный, так как
см. Опустим перпендикуляр CH на сторону AD. Тогда треугольник CHD — прямоугольный равнобедренный, так как 

 а ABCH — прямоугольник, значит
а ABCH — прямоугольник, значит 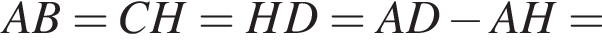
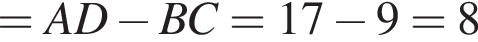
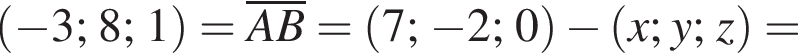
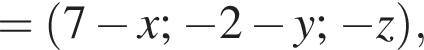
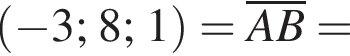
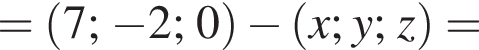
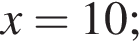
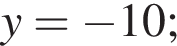
 Найдем произведение векторов:
Найдем произведение векторов: 
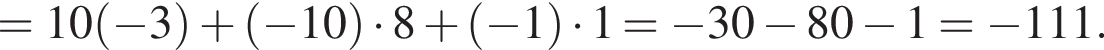

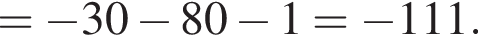
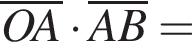
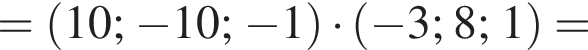
 тогда
тогда 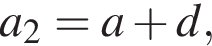
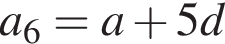 и по условию
и по условию 
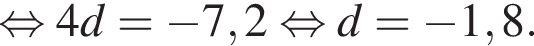
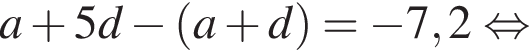
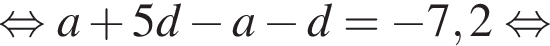
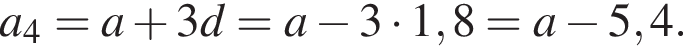
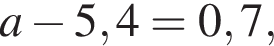 откуда
откуда 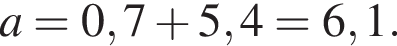
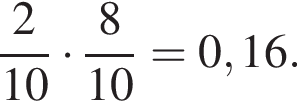 Вероятность того, что для получения следующей принцессы Маше придётся купить 3 шоколадных яйца, равна
Вероятность того, что для получения следующей принцессы Маше придётся купить 3 шоколадных яйца, равна 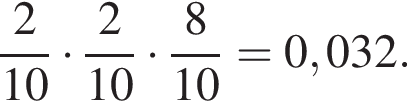 Таким образом, искомая вероятность — 0,16 + 0,032 = 0,192.
Таким образом, искомая вероятность — 0,16 + 0,032 = 0,192.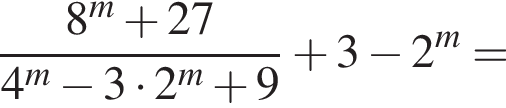
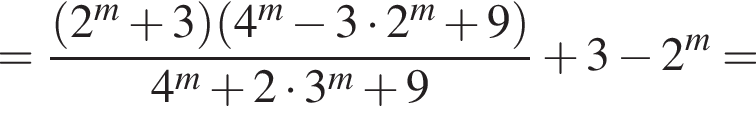
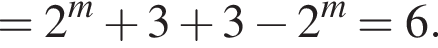
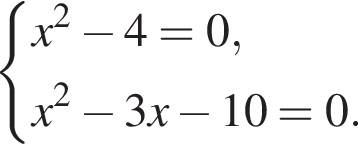
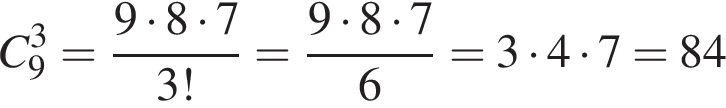
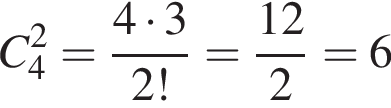 способов выбрать два тюльпана из четырех. Любой из первых способов можно совместить с любым из вторых, поэтому общее число способов равно
способов выбрать два тюльпана из четырех. Любой из первых способов можно совместить с любым из вторых, поэтому общее число способов равно 
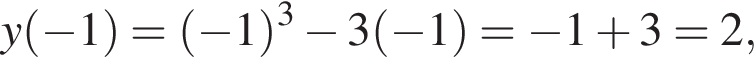
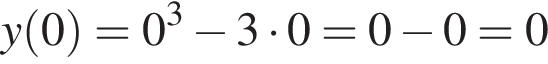
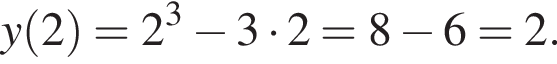
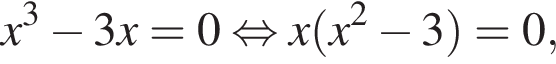 откуда
откуда 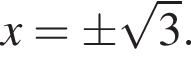 Возьмем производную функции:
Возьмем производную функции: 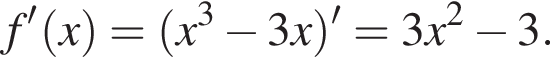
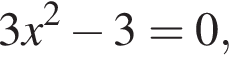 получим
получим 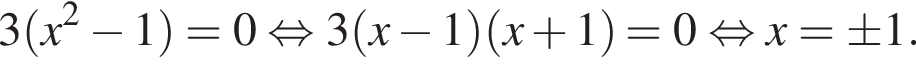
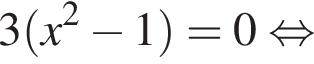
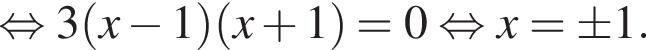
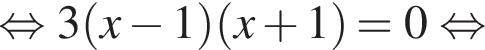

 и при
и при  (функция убывает). При
(функция убывает). При 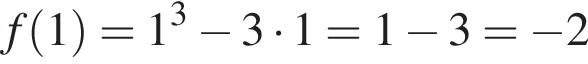
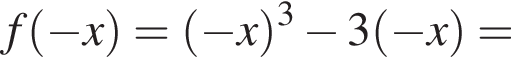
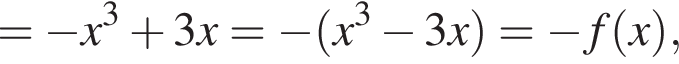
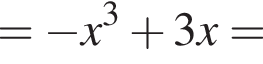
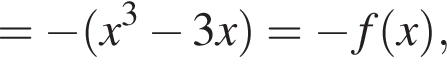
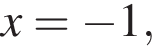 то
то 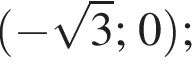
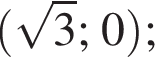
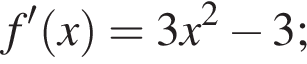


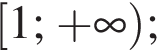 проміжок спадання: [−1; 1]; точки екстремуму:
проміжок спадання: [−1; 1]; точки екстремуму: 
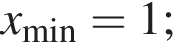 екстремуми:
екстремуми: 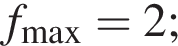

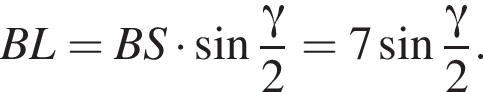
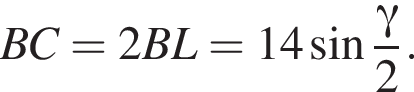 Апофема треугольника BSC равна
Апофема треугольника BSC равна 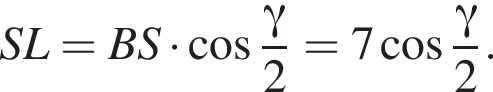
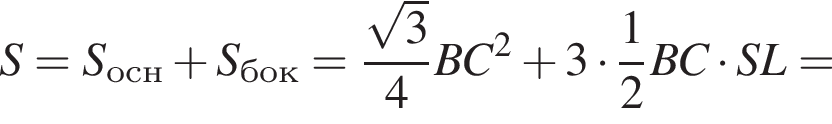
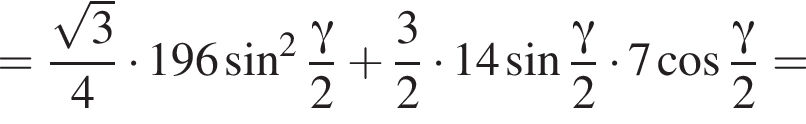
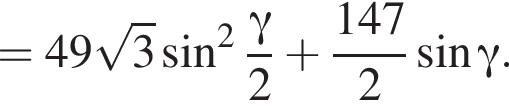
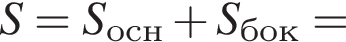
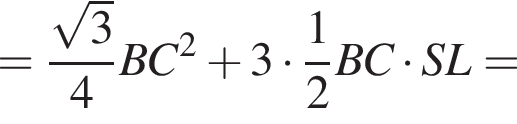
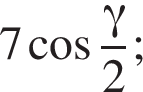 3)
3) 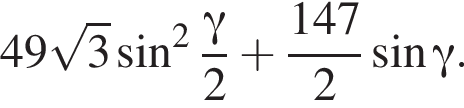
 то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
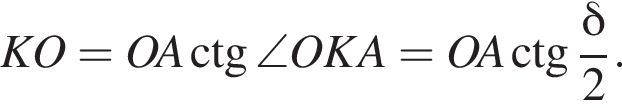
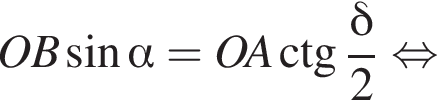
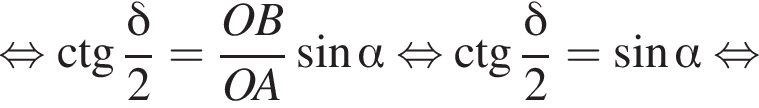
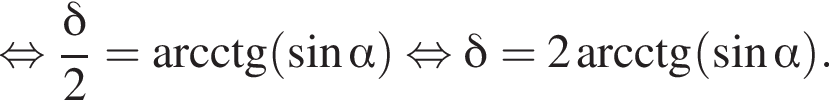
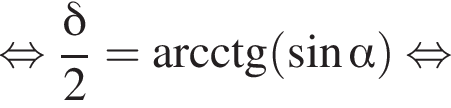

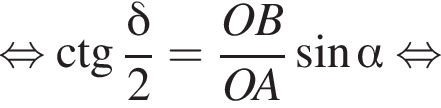
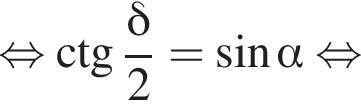
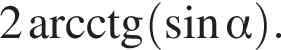
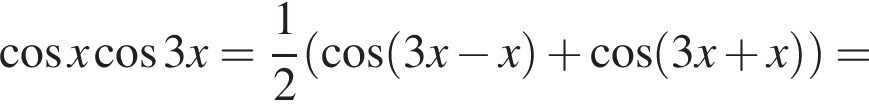
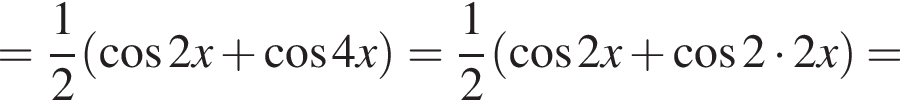
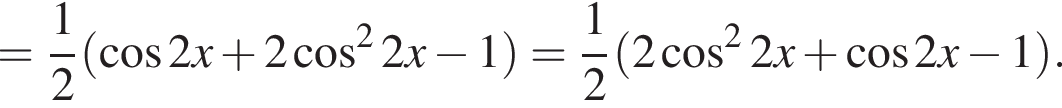
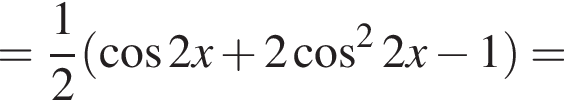
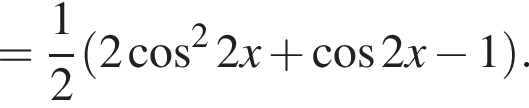
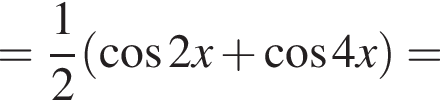
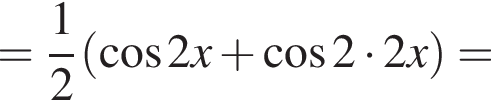

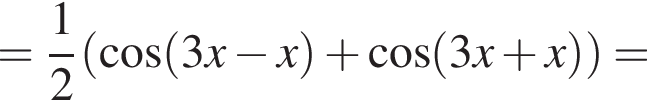
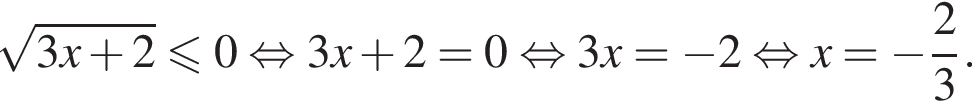

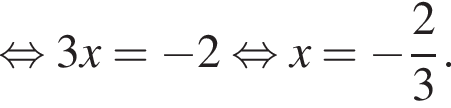
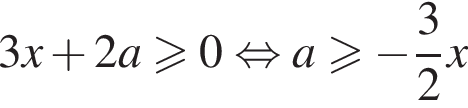
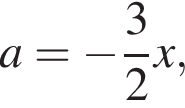 включая эту прямую.
включая эту прямую.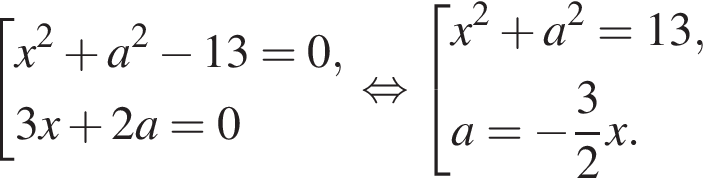
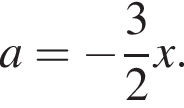
 — верно.
— верно. — неверно.
— неверно.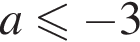 неравенство имеет одно решение, при
неравенство имеет одно решение, при 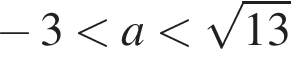 неравенство имеет бесконечное число решений, при
неравенство имеет бесконечное число решений, при 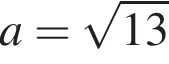 неравенство имеет два решения, при
неравенство имеет два решения, при 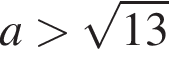 неравенство имеет одно решение.
неравенство имеет одно решение.