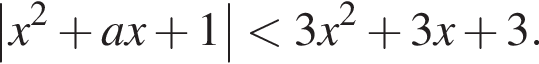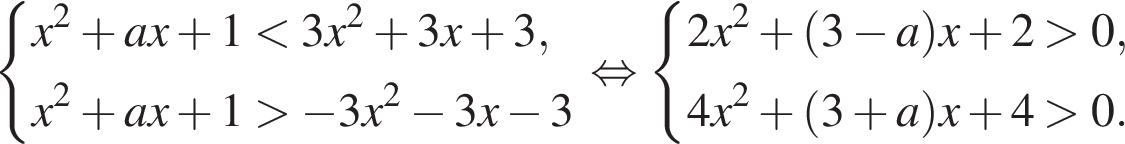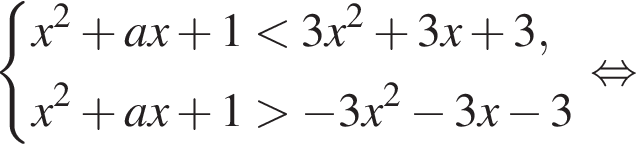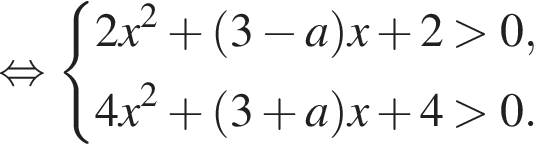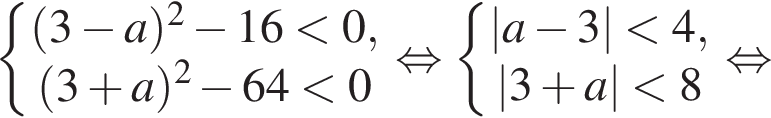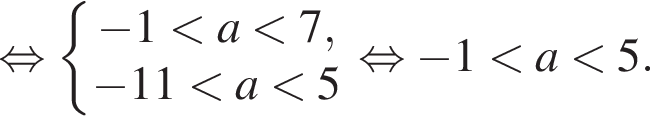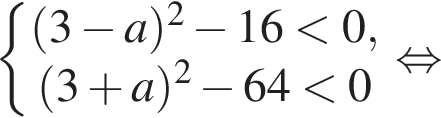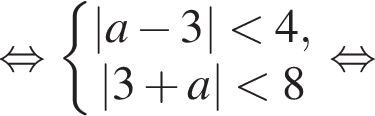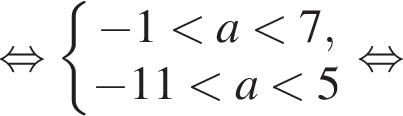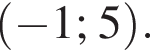Кількість відвідувачів ботанічного саду протягом червня становила чверть від їхньої сумарної кількості в травні й червні. На якій із діаграм правильно зображено розподіл відвідувачів цього ботанічного саду впродовж цих двох місяців?
Поїзд Львів-Одеса вирушає о 15:20, а прибуває о 4:20 наступного дня. Скільки годин поїзд перебуває в дорозі?
Визначте об’єм правильної трикутної призми, бічні грані якої є квадратами, а периметр основи дорівнює 12.
Розв'яжіть рівняння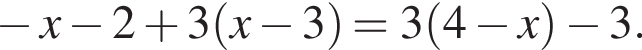
Сума трьох кутів паралелограма дорівнює 280°. Визначте градусну міру більшого кута цього паралелограма.
На рисунку зображено графік функції
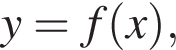 яка визначена на відрізку [−4; 3]. Укажіть область значень цієї функції.
яка визначена на відрізку [−4; 3]. Укажіть область значень цієї функції.
Спростiть вираз 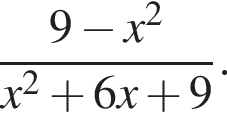
Щоб перевести значення температури за шкалою Цельсія ( t ° C ) в шкалу Фаренгейта ( t ° F ), користуються формулою F = 1,8 C + 32 де C - градуси Цельсія, F - градуси Фаренгейта. Яка температура за шкалою Цельсія відповідає 6° за шкалою Фаренгейта? Відповідь округліть до десятих.
Якщо числа х і у задовольняють співвідношення 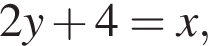 то y?
то y?
Які з таких тверджень вірні?
I. Навколо будь-якого трикутника можна описати коло.
ІІ. Якщо в паралелограмі діагоналі рівні і перпендикулярні, цей паралелограм — квадрат.
ІІІ. Площа трапеції дорівнює добутку середньої лінії на висоту.
Розв'яжіть рівняння 
Укажіть похідну функції 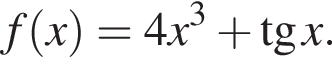
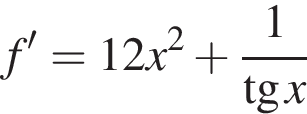
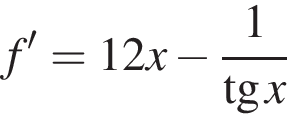
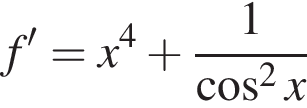
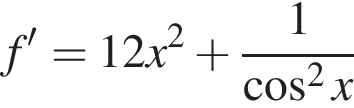
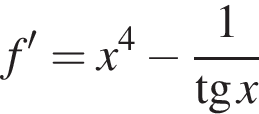
Розв’яжіть систему нерівностей: 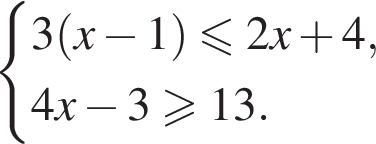
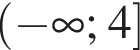

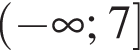
Спростіть вираз 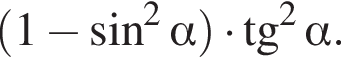
У правильній чотирикутній піраміді SABCD точка O — центр основи, S вершина, SO = 4, AC = 6. Знайдіть бічне ребро SC.
Автомобіль, задні дверцята якого відкриваються так, як зображено на рисунку, під’їжджає заднім ходом по горизонтальній поверхні CA перпендикулярно до вертикальної стіни AB. Укажіть серед наведених найменшу відстань й від автомобіля до стіни AB, за якої задні дверцята автомобіля зможуть із зачиненого стану KP безперешкодно набувати зображеного на рисунку положення KP'. Тоді
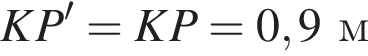 i
i 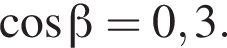 Наявністю заднього бампера автомобіля знехтуйте.
Наявністю заднього бампера автомобіля знехтуйте.
Установіть відповідність між функцією (1−4) та координатними чвертями (А−Д), у яких розміщений графік цієї функції (координатні чверті показано на рисунку).
1. 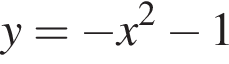
2. 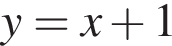
3. 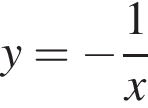
4. 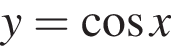
А II та IV
Б III та IV
В І, II те III
Г І, III та IV
Д І, ІІ, III та IV
Установіть відповідність між твердженням про дріб (1−4) та дробом (А−Д), для якого це твердження є правильним.
1. є скоротним
2. є неправильним
3. менший за 0,5
4. є оберненим до дробу ![]()
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Установіть відповідність між геометричною фігурою (1—4) та її площею (А—Д).
1. ромб зі стороною 6 см і тупим кутом 120°
2. квадрат, у який уписане коло радіуса 2 см
3. паралелограм, одна сторона якого дорівнює 5 см, а висота, проведена з вершини
тупого кута, ділить іншу сторону на відрізки завдовжки 4 см i 12 см
4. прямокутник, більша сторона якого дорівнює 6 см й утворює з діагоналлю кут 30°
фігури
А 12 см2
Б 16 см2
В 18 см2
Г 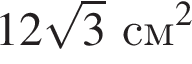
Д 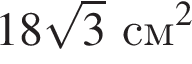
Установіть відповідність між геометричним тілом (1—4) і його об’ємом (А—Д).
1. циліндр, діаметр основи та висота якого дорівнюють a (рис. 1)
2. конус, діаметр основи та висота якого дорівнюють a (рис. 2)
3. куля, діаметр якої дорівнює a (рис. 3)
4. правильна трикутна призма, сторона основи та
бічне ребро якої дорівнюють відповідно a i ![]() (рис. 4)
(рис. 4)
А ![]()
Б ![]()
В ![]()
Г 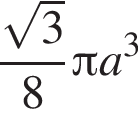
Д ![]()
Для визначення ширини автомагістралі hмаг, (у м) що має по 4 однакові смуги руху
транспорту в обох напрямках (див. рисунок), використовують формулу 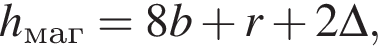 де
де
b — ширина однієї смуги руху транспорту;
r — ширина розділювальної смуги між напрямками руху транспорту;
![]() — ширина запобіжної смуги між крайньою смугою руху й бордюром.
— ширина запобіжної смуги між крайньою смугою руху й бордюром.
1. Визначте ширину b (у м) однiєї смуги, якщо 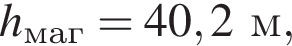 r = 10 м,
r = 10 м, 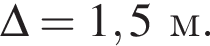
2. Заплановано збільшити ширину b кожної смуги руху транспорту на 10% за рахунок лише зменшення ширини r розділювальної смуги. На скільки метрів потрібно зменшити ширину r розділювальної смуги?
У прямокутному трикутнику ABC
 відстані від середини медіани BM до катетів АС і BC дорівнюють 5 см і 6 см відповідно.
відстані від середини медіани BM до катетів АС і BC дорівнюють 5 см і 6 см відповідно.
1. Визначте довжину катета AC (у см).
2. Визначтеї радіус (у см) кола, описаного навколо трикутника ABC.
В прямоугольной системе координат на плоскости задан вектор 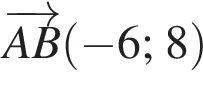 с началом в точке A(2; -4).
с началом в точке A(2; -4).
1. Найдите координаты точки B. В ответе запишите их произведение.
2. Вычислите модуль вектора 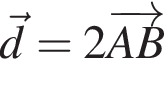
Дана геометрична прогресія ( bn ), знаменник якої дорівнює 2 а 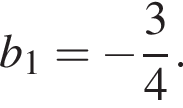
1. Знайдіть суму перших шести її членів.
2. Найдите разность между шестым и третьим членом этой прогрессии.
За відгуками покупців Іван Іванович оцінив надійність двох інтернет-магазинів. Ймовірність того, що потрібний товар доставлять із магазину А, дорівнює 0,8. Ймовірність того, що цей товар доставлять із магазину Б, дорівнює 0,9. Іван Іванович замовив товар одразу в обох магазинах. Вважаючи, що інтернет-магазини працюють незалежно один від одного, знайдіть ймовірність того, що жоден магазин не доставить товар.
Лідія редагує 80 сторінок рукопису у 8 разів швидше, ніж Максим редагує 480 сторінок. Скільки сторінок відредагує Максим за той самий час, за який Лідія відредагує 320 сторінок? Уважайте, що продуктивність роботи і Лідії, і Максима є сталою.
Обчисліть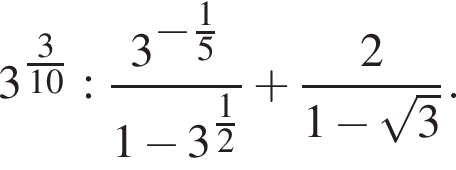
Розв'яжіть рівняння У відповіді запишіть добуток усіх його дійсних коренів.
У відповіді запишіть добуток усіх його дійсних коренів.
Компанія з 6 дорослих, з яких лише двоє мають відповідні посвідчення водія, сідають в автомобіль, у якому окрім місця водія є ще 5 пасажирських місць.
Скільки всього є способів у цих 6 осіб зайняти місця в автомобілі, якщо на місці водія має бути особа з відповідним посвідченням?
| x | y |
|---|---|
| 0 | |
| 1 | |
| 2 |
Задано функцію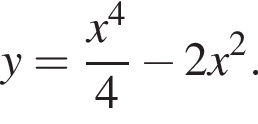
1. Для наведених у таблиці значень аргументів х визначте відповідні їм значення у (див. таблицю).
2. Визначте та запишіть координати точок перетину графіка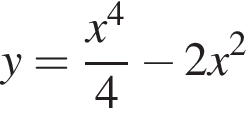 з віссю x .
з віссю x .
3. Знайдіть похідну f' функції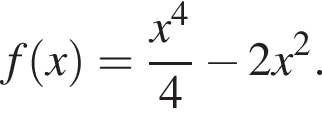
4. Визначте нулі функції f' .
5. Визначте проміжки зростання та спадання, точки екстремуму функції f .
6. Побудуйте ескіз графіка функції f .
Осьовим перерізом циліндра є прямокутник ABCD, сторона AD якого лежить у нижній основі циліндра. Діагональ AC перерізу утворює з площиною верхньої основи циліндра кут β. Діаметр основи циліндра дорівнює d.
1. Зобразіть на рисунку заданий циліндр і його осьовий переріз ABCD.
2. Укажіть кут β, що утворює пряма AC з площиною верхньої основи циліндра.
3. Визначте об’єм циліндра.
Осьовим перерізом циліндра є прямокутник ABCD, сторона AD якого лежить у нижній основі циліндра. Діагональ АС перерізу утворює з площиною верхньої основи циліндра кут β. Діаметр основи циліндра дорівнює d. На колі нижньої основи вибрано точку K так, що відрізок AK видно з точки D під кутом 30°.
1. Зобразіть на рисунку заданий циліндр і вкажіть кут у між площиною (CKA) і площиною нижньої основи. Обґрунтуйте його положення.
2. Визначте кут γ.
Доведіть нерівність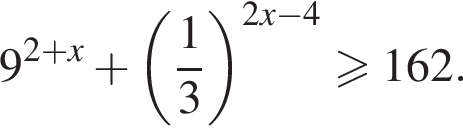
Задано нерівність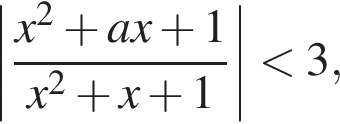 де x – змінна, a – параметр.
де x – змінна, a – параметр.
1. Розв'яжіть нерівність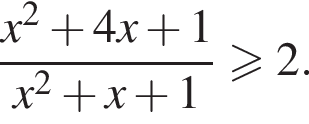
2. Знайдіть усі значення a , при кожному з яких нерівність виконується за всіх x .

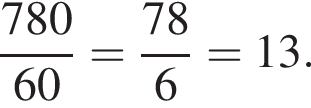
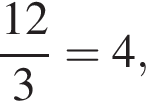 такая же и высота у призмы. Площадь основания равна
такая же и высота у призмы. Площадь основания равна 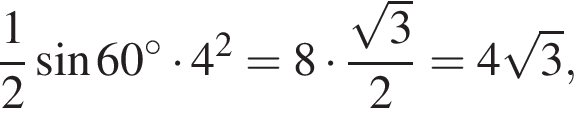
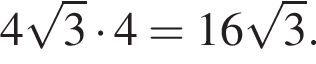

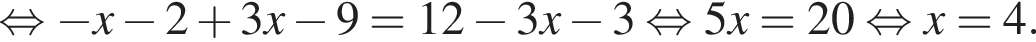
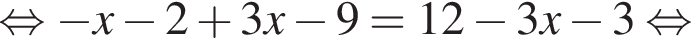
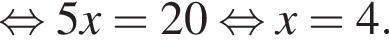
 Тогда другой угол параллелограмма равен
Тогда другой угол параллелограмма равен 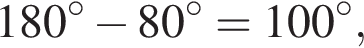 поскольку соседние углы параллелограмма всегда дают в сумме 180°. Ясно, что 100° и есть наибольший угол.
поскольку соседние углы параллелограмма всегда дают в сумме 180°. Ясно, что 100° и есть наибольший угол.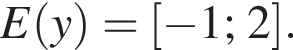
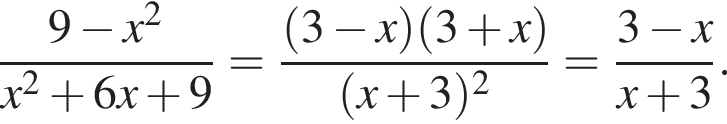
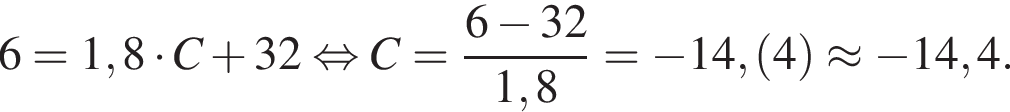

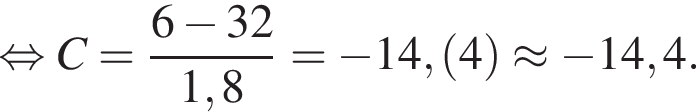
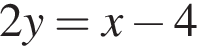 и
и 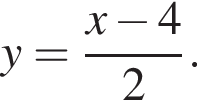
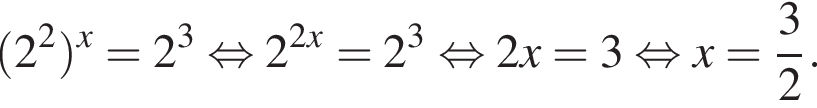

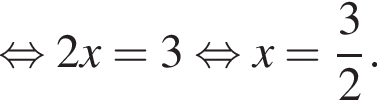
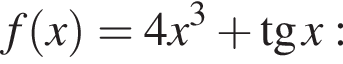
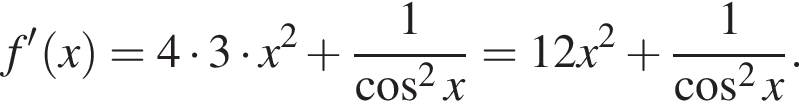
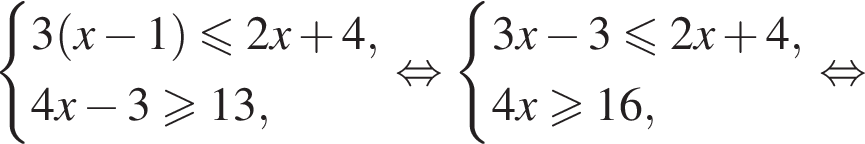
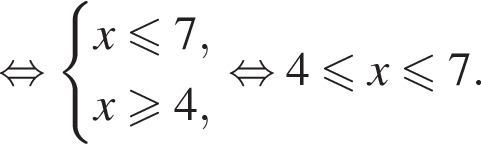
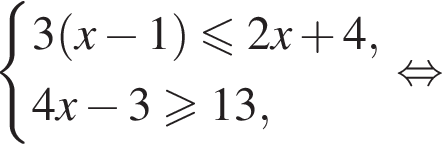
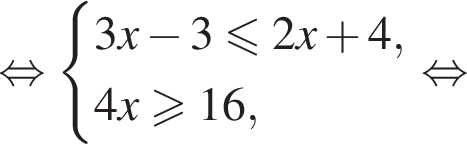
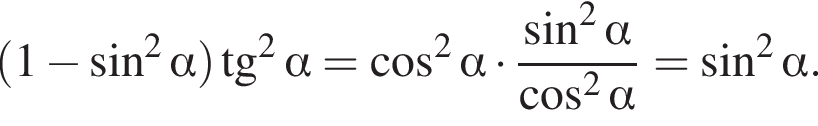
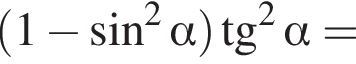
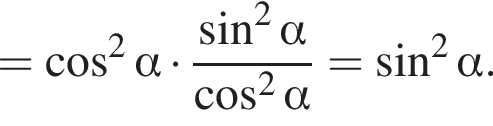
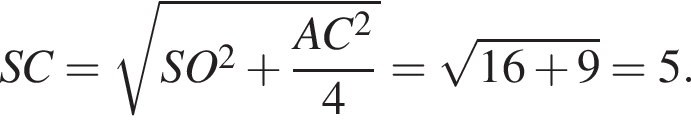
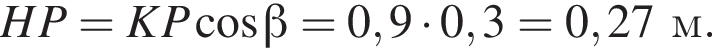
 от P. Поэтому расстояние до стены должно быть не менее 0,63 м. Минимально подходящее расстояние из предложенных — 0,7 м.
от P. Поэтому расстояние до стены должно быть не менее 0,63 м. Минимально подходящее расстояние из предложенных — 0,7 м.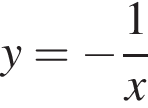 при положительных x принимает отрицательные значения, то есть ее график не проходит через первую четверть. Такой вариант остался один (А).
при положительных x принимает отрицательные значения, то есть ее график не проходит через первую четверть. Такой вариант остался один (А). 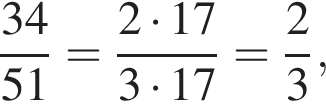 у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.
у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.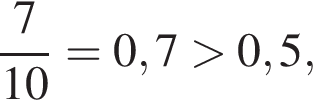
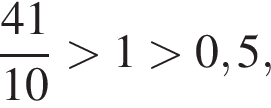
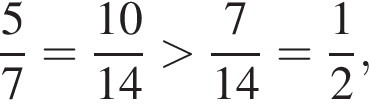
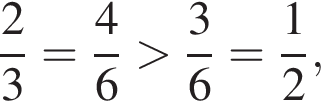
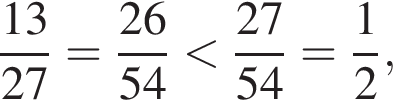
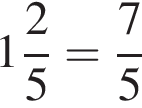 будет дробь
будет дробь 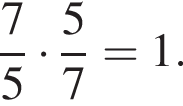
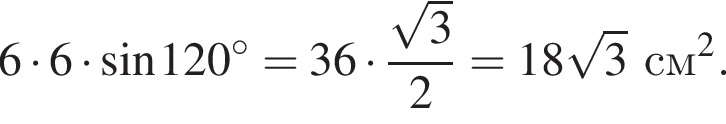
 см2
см2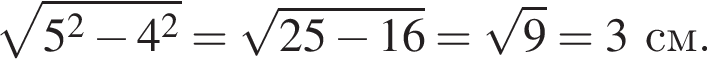
 см2
см2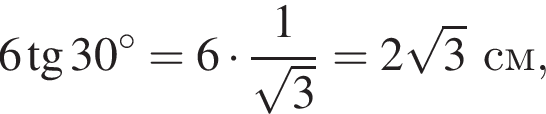
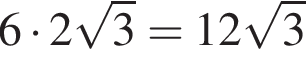 см2.
см2. где
где  Получаем:
Получаем: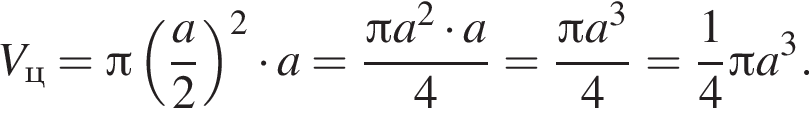
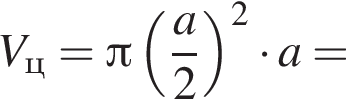
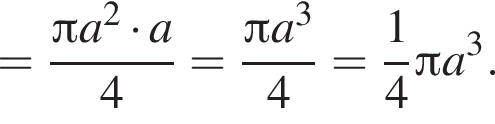
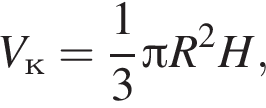 где
где  Получаем:
Получаем: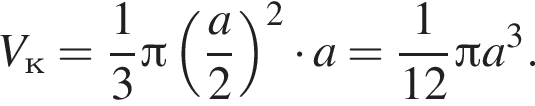
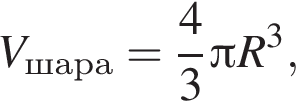 где
где 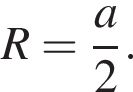 Получаем:
Получаем: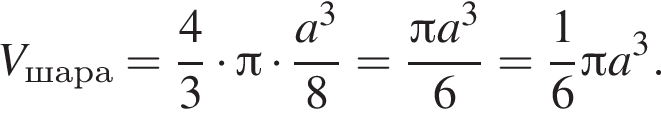
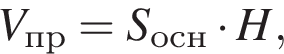 где
где 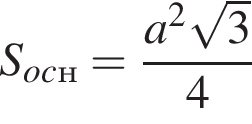 (основа — правильный треугольник со стороной a),
(основа — правильный треугольник со стороной a), 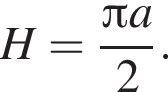 Получаем:
Получаем: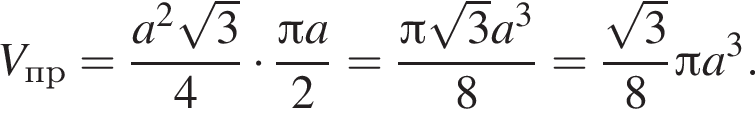
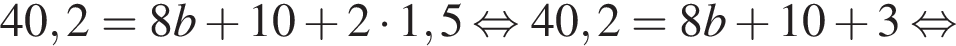

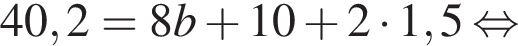

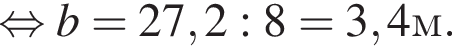
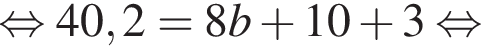

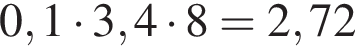 метра, которые придется отобрать у разделительной полосы.
метра, которые придется отобрать у разделительной полосы. м
м см
см см.
см.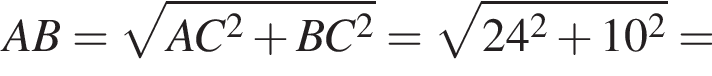

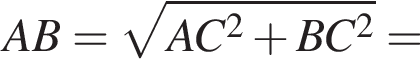
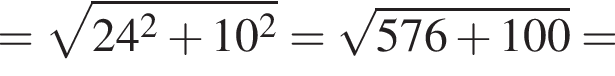
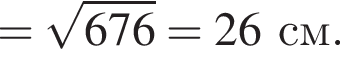
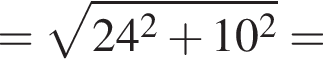
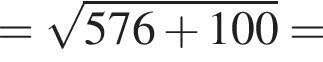
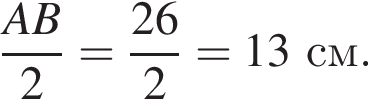
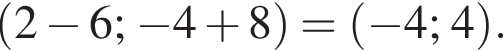
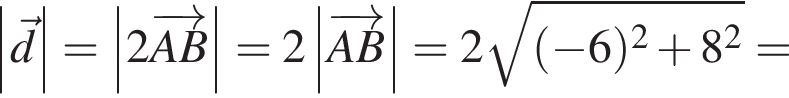
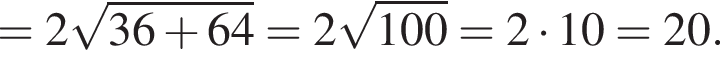
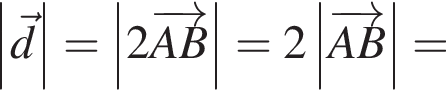
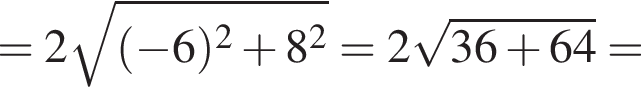

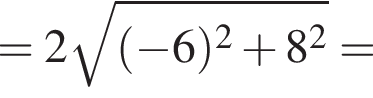
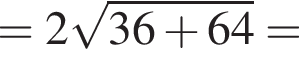
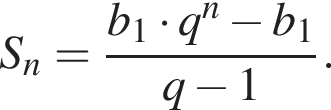
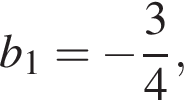
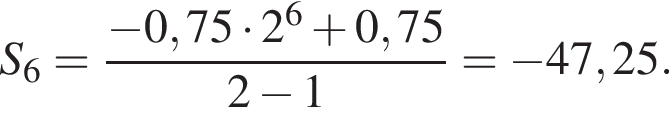
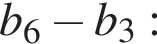
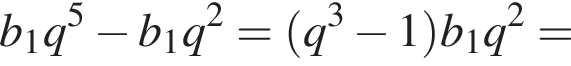
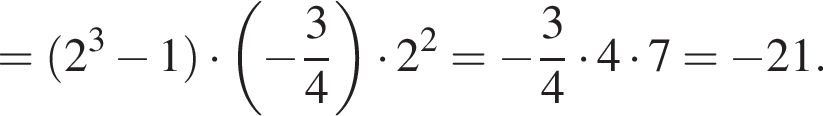
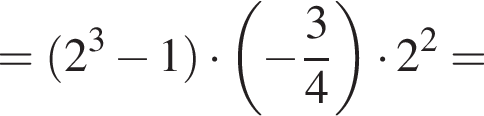
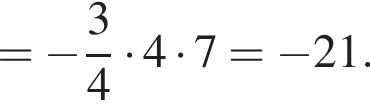
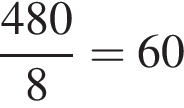 страниц, то есть ее скорость в
страниц, то есть ее скорость в 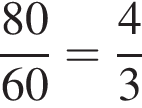 раза выше. Значит, пока она отредактирует 320 страниц, Максим отредактирует количество страниц, равное
раза выше. Значит, пока она отредактирует 320 страниц, Максим отредактирует количество страниц, равное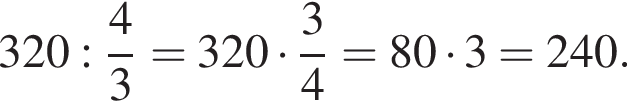
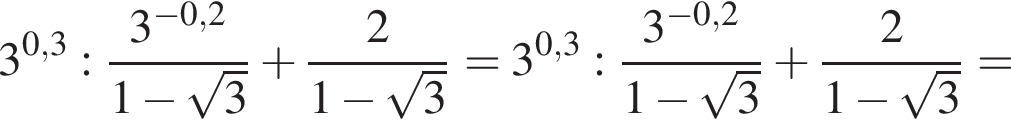
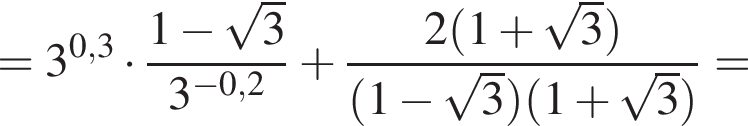
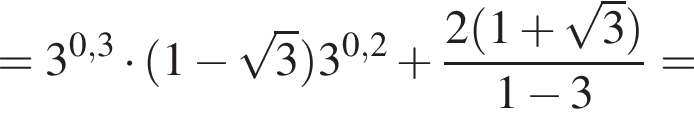
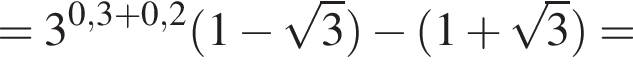
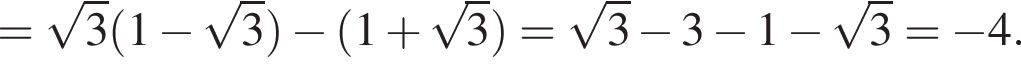
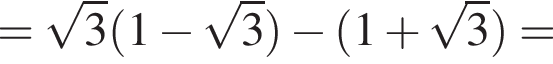
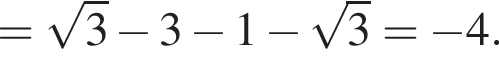
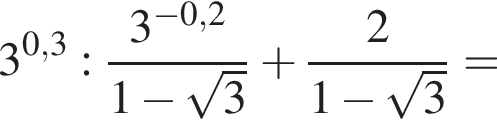
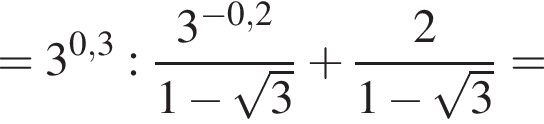
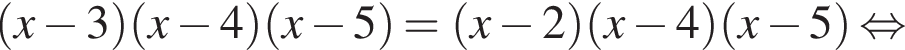
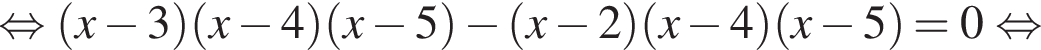
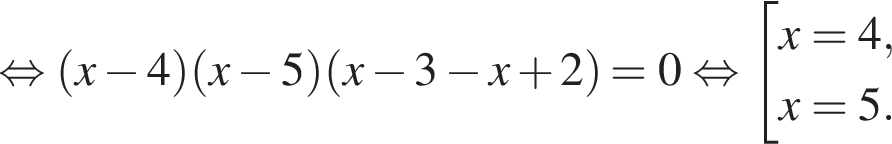
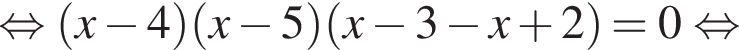
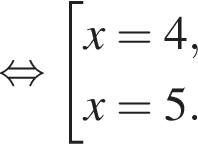
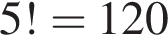 способов. Окончательный ответ
способов. Окончательный ответ  способов.
способов.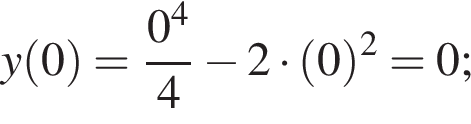
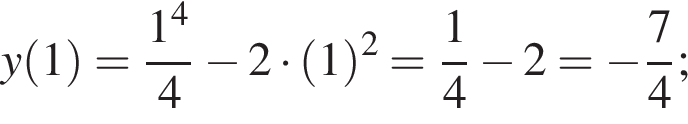
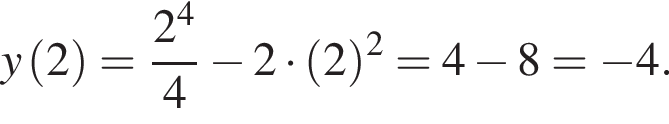
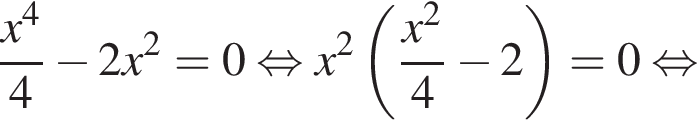
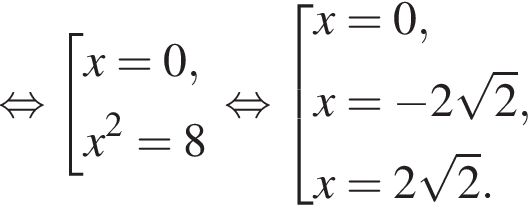
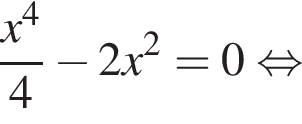
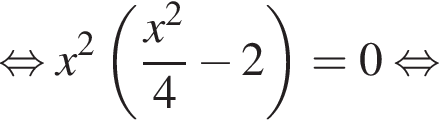
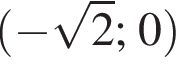 и
и 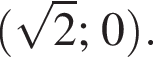 Промежутки знакопостоянтсва отметим на рисунке.
Промежутки знакопостоянтсва отметим на рисунке. 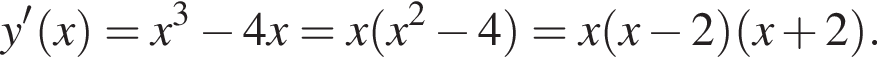
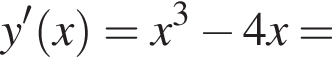
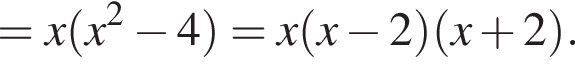
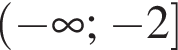 и на
и на 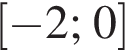 и на
и на 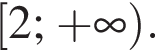
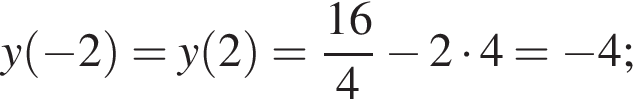
 График функции изображен на рисунке.
График функции изображен на рисунке.  поэтому
поэтому 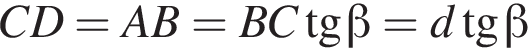
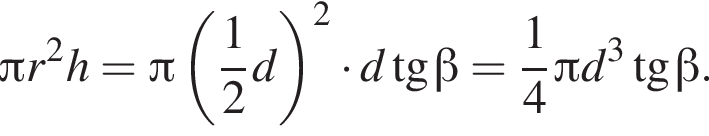
 а
а  поскольку опирается на диаметр, то
поскольку опирается на диаметр, то 
 Значит,
Значит, 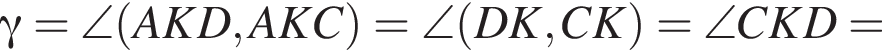
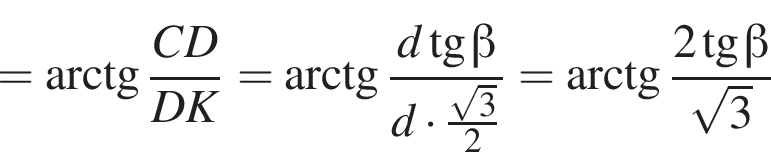

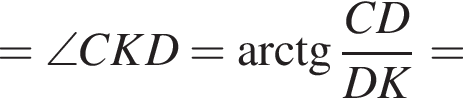
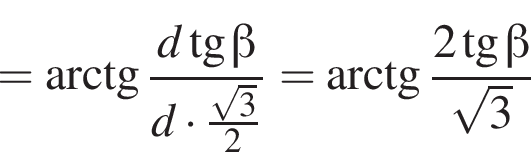

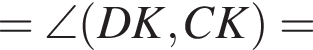
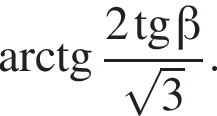
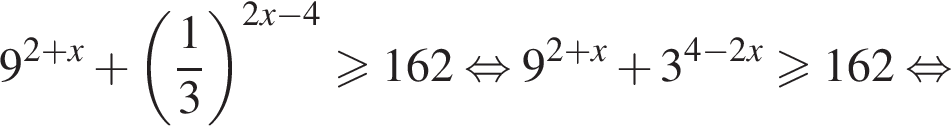
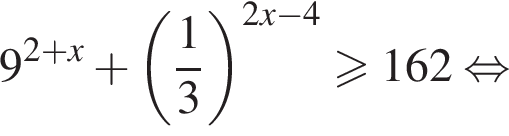
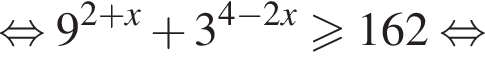
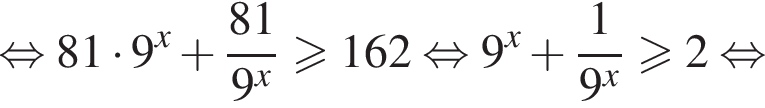

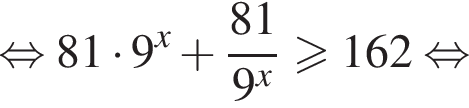
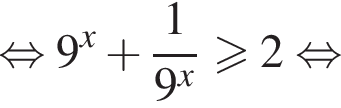
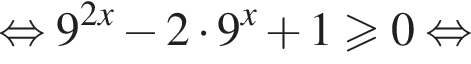
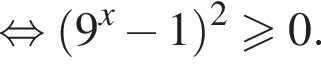
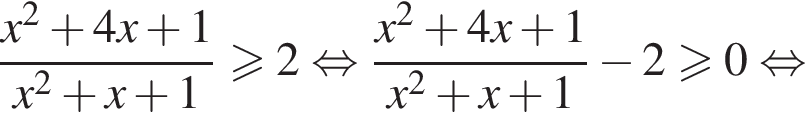
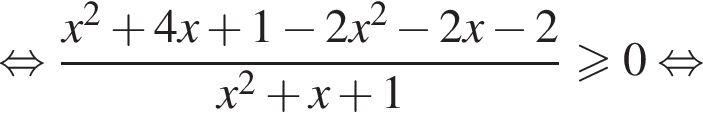
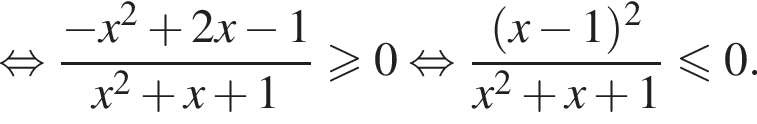
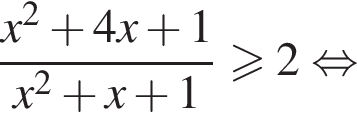
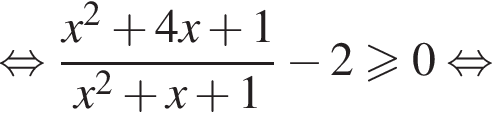
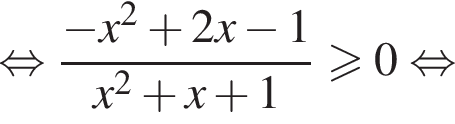
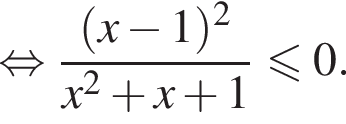
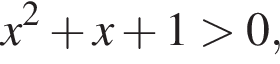 то надо решить неравенство
то надо решить неравенство 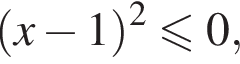 откуда
откуда 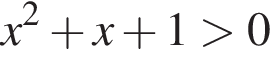 для всех значений x, получаем:
для всех значений x, получаем: