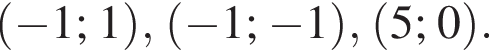На рисунку жирними точками позначено річні мінімуми площі поверхні арктичного льоду, що спостерігалися в період з 2004 р. по 2014 р. (для наочності точки з’єднано відрізками). По горизонталі відмічено роки, а по вертикалі — площу поверхні льоду (у млн км2). Користуючись наведеною інформацією, визначте із вказаного періоду рік, у якому величина річного мінімуму площі поверхні льоду змінилась найбільше порівняно з попереднім роком.
Два фахівці розробили макет рекламного оголошення. За роботу вони отримали 3000 грн i розподілили гроші таким чином: перший отримав четверту частину зароблених грошей, а другий — решту. Скільки гривень отримав за цю роботу другий фахівець?
На рисунку зображено куб ABCDA1B1C1D1. Яка з наведених прямих паралельна площині (AA1B1)?
Обчисліть добуток коренів рівняння 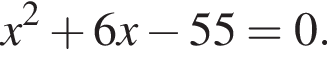
На рисунку зображено рівнобедрений трикутник ABC
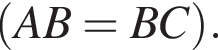 Визначте градусну міру кута BAC, якщо
Визначте градусну міру кута BAC, якщо 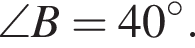
На рисунку зображено графік функції
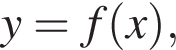 визначеної на проміжку' [−3; 2]. Укажіть точку перетину графіка функції
визначеної на проміжку' [−3; 2]. Укажіть точку перетину графіка функції 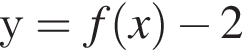 з віссю y.
з віссю y.
Знайти 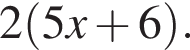

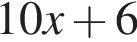

Якщо ціна паркету (p) пов'язана із ціною деревини для його виробництва (d) співвідношенням  то d дорівнює?
то d дорівнює?
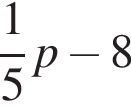

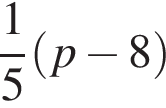

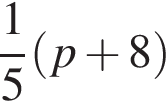
Спростіть вираз 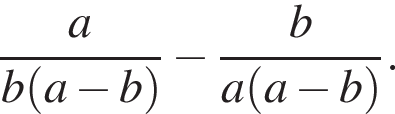
На рисунку зображено паралелограм ABCD. Які з наведених тверджень є правильними?
I. 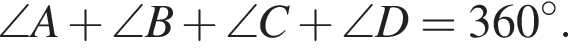
II. 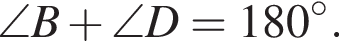
III. 
Розв’яжіть рівняння 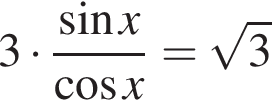
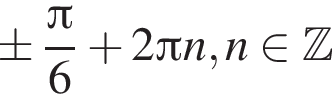
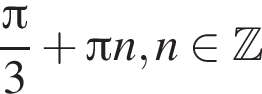
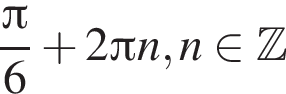
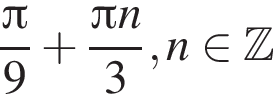
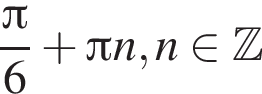
Укажіть рівняння прямої, яка може бути дотичною до графіка функції 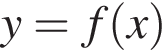 у точці з абсцисою
у точці з абсцисою  якщо
якщо 
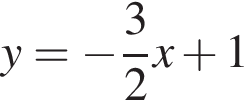
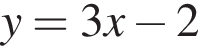

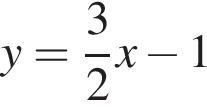
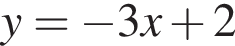
Розв'яжіть нерівність 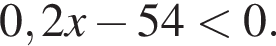
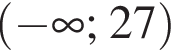
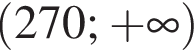
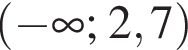
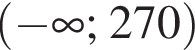
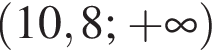
Спростіть вираз 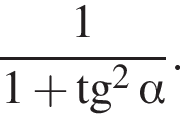
Висота правильної чотирикутної піраміди дорівнює 3 см, а сторона ї основи 12 см. Знайдіть довжину бічного ребра піраміди.
Лист заліза, щоо має форму прямокутника ABCD
 згортають таким чином, щоб отримати циліндричну трубу (див. лівий і правий рисунки). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнюе 20 см. Виберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварювання знехтуйте.
згортають таким чином, щоб отримати циліндричну трубу (див. лівий і правий рисунки). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнюе 20 см. Виберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварювання знехтуйте.
Установіть відповідність між функцією (1−4) та координатними чвертями (А−Д), у яких розміщений графік цієї функції (координатні чверті показано на рисунку).
1. 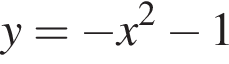
2. 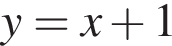
3. 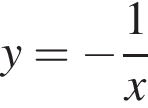
4. 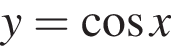
А II та IV
Б III та IV
В І, II те III
Г І, III та IV
Д І, ІІ, III та IV
Установіть відповідність між твердженням про дріб (1−4) та дробом (А−Д), для якого це твердження є правильним.
1. є скоротним
2. є неправильним
3. менший за 0,5
4. є оберненим до дробу ![]()
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Установіть відповідність між геометричною фігурою (1−4) та її площею (А−Д).
1. круг радіуса 4 см (рис. 1)
2. півкруг радіуса 6 см (рис. 2)
3. сектор радіуса 12 см з градусною мірою центрального кута 30* (рис. 3)
4. кільце, обмежене колами радіусів 4 см і 6 см (рис. 4)
А 12π см2
Б 16π см2
В 18π см2
Г 20π см2
Д 24π см2
У прямокутній декартовій системі координат xyz у просторі задано точку М (1; −4; 8). Установіть відповідність між початком речення (1−4) та його закінченням (А−Д) так, щоб утворилося правильне твердження.
1. Відстань від точки M до площини ху дорівнює
2. Відстань від точки M до початку координат дорівнює
3. Відстань від точки M до осі z дорівнює
4. Відстань від точки M до N (1; 0; 8) дорівнює
А 1
Б 4
В ![]()
Г 8
Д 9
У магазині в продажу є лише музичні диски, диски з науково-популярними фільмами та диски з художніми фільмами. Кількість дисків із науково-популярними фільмами в п'ять разів більша за кількість музичних дисків і вдвічі менша за кількість дисків із художніми фільмами. Загальна кількість дисків у цьому магазині дорівнює 192.
1. Скільки відсотків становить кількість музичних дисків від загальної кількості всіх дисків у магазині?
2. Визначте кількість дисків із науково-популярними фільмами в цьому магазині.
З вершини тупого кута В паралелограма ABCD опущено перпендикуляр ВО на сторону AD. Коло з центром у точці A проходить через вершину B та перетинає сторону AD в точці K. Відомо, що 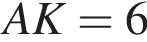 см,
см, см,
см, см.
см.
1. Визначте периметр паралелограма ABCD (у см).
2.Обчисліть довжину діагоналі BD (у см).
В прямоугольной системе координат в пространстве заданы векторы 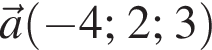 и
и 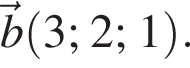
1. Укажите координаты вектора 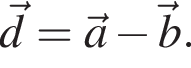 В ответе запишите их произведение.
В ответе запишите их произведение.
2. Обчисліть скалярний добуток ![]()
В арифметичній прогресії (an) відомо, що а2 = 1, а4 = 9.
1. Визначте рiзницю цiєї прогресiї.
2. Обчислигь суму S20 двадцяти перших членiв цiєї прогресiї.
На діаграмі відображено інформацію про результати складання письмового заліку студентами певної групи. Комісія з якості освіти розпочинає перевірку відповідності виставлених оцінок змісту залікових робіт студентів і відбирає для перевірки декілька робіт навмання. Яка ймовірність того, що першою буде відібрано роботу з оцінкою D? Отриману відповідь округліть до сотих.
Човен проходить 24 км за течією ріки за
Обчисліть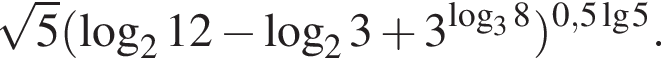
Розв'яжіть рівняння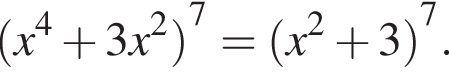 У відповідь запишіть суму всіх його дійсних коренів.
У відповідь запишіть суму всіх його дійсних коренів.
У фінал пісенного конкурсу вийшло 4 солісти та 3 гурти. Порядковий номер виступу фіналістів визначають жеребкуванням. Скільки всього є варіантів послідовностей виступів фіналістів, якщо спочатку виступатимуть гурти, а після них — солісти?
Уважайте, що кожен фіналіст виступатиме у фіналі лише один раз.
| x | y |
|---|---|
| −1 | |
| 0 | |
| 2 |
Задано функцію 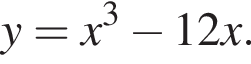
1. Для наведених у таблиці значень аргументи х визначте відповідні їм значення у (см. тблицу).
2. Визначте й запишіть координати точок перетину графіка функції 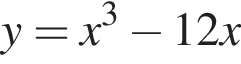 із віссю х.
із віссю х.
3. Знайдіть похідну f' функції 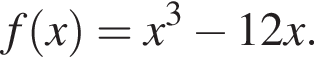
4. Визначте нулі функції f'.
5. Визначте проміжки зростання і спадання, точки екстремуму й екстремуми функції f.
6. Побудуйте ескіз графіка функції f.
Осьовим перерізом циліндра є прямокутник ABCD, сторона AD якого лежить у нижній основі циліндра. Діагональ AC перерізу утворює з площиною верхньої основи циліндра кут β. Діаметр основи циліндра дорівнює d.
1. Зобразіть на рисунку заданий циліндр і його осьовий переріз ABCD.
2. Укажіть кут β, що утворює пряма AC з площиною верхньої основи циліндра.
3. Визначте об’єм циліндра.
Осьовим перерізом циліндра є прямокутник ABCD, сторона AD якого лежить у нижній основі циліндра. Діагональ АС перерізу утворює з площиною верхньої основи циліндра кут β. Діаметр основи циліндра дорівнює d. На колі нижньої основи вибрано точку K так, що відрізок AK видно з точки D під кутом 30°.
1. Зобразіть на рисунку заданий циліндр і вкажіть кут у між площиною (CKA) і площиною нижньої основи. Обґрунтуйте його положення.
2. Визначте кут γ.
Доведіть тотожність
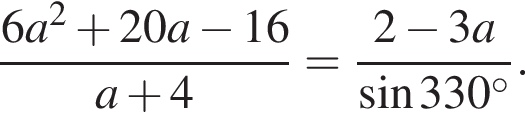
Задано систему рівнянь
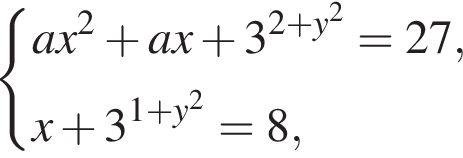
де х, у — змінні, a — стала.
1. Розв’яжіть цю систему, якщо ![]()
2. Визначте всі розв’язки заданої системи залежно від значень а.

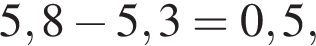 за 2007 —
за 2007 — 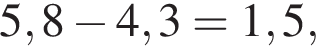 за 2009 —
за 2009 — 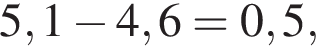 за 2012 —
за 2012 — 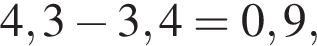 за 2013 —
за 2013 — 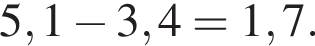 Это последнее и есть наибольшее.
Это последнее и есть наибольшее.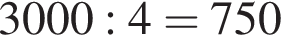 гривен, значит второй — оставшиеся
гривен, значит второй — оставшиеся  гривен.
гривен.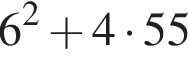 положителен. По теореме Виета их произведение равно его свободному члену, то есть −55.
положителен. По теореме Виета их произведение равно его свободному члену, то есть −55. По теореме о сумме углов треугольника получаем:
По теореме о сумме углов треугольника получаем: 

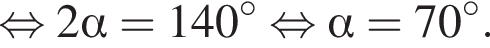
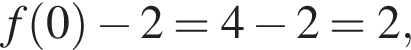 точкой пересечения будет (0; 2). То, что
точкой пересечения будет (0; 2). То, что  видно из графика f(x).
видно из графика f(x).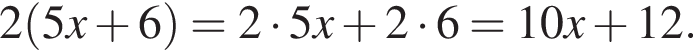
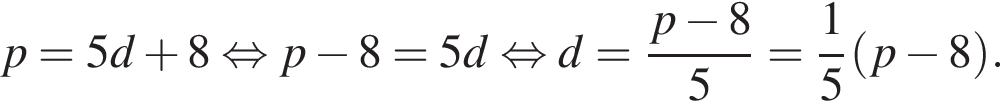

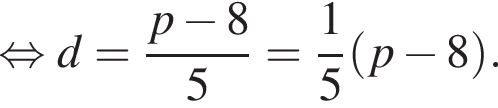
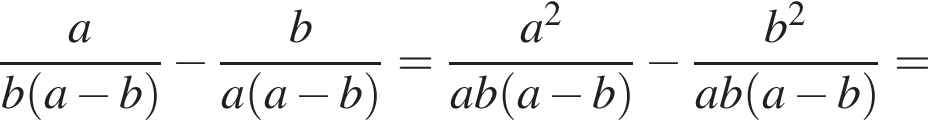
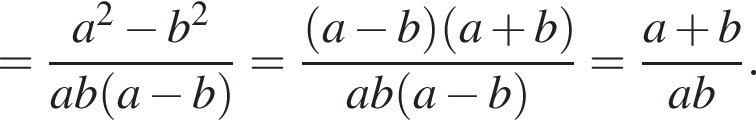
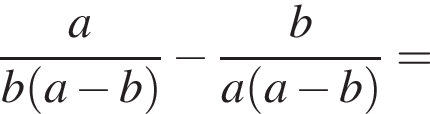
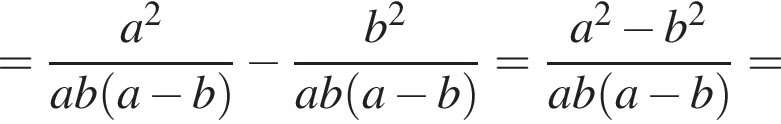
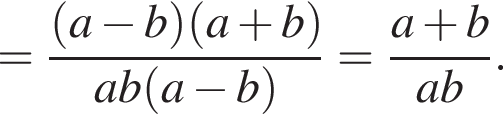
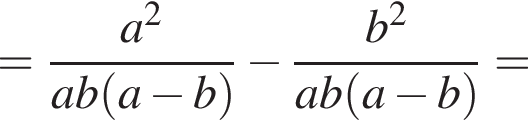
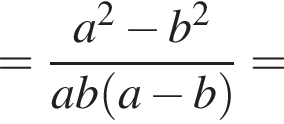
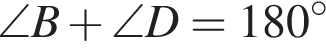 равносильно утверждению
равносильно утверждению  то есть
то есть  Это на рисунке не выполнено. Наконец,
Это на рисунке не выполнено. Наконец,  а
а  поэтому
поэтому 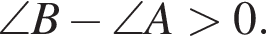 Окончательно, верны утверждения 1 и 3.
Окончательно, верны утверждения 1 и 3.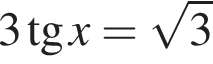 или
или 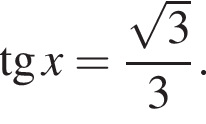 Получим
Получим 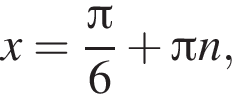
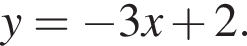
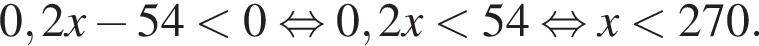
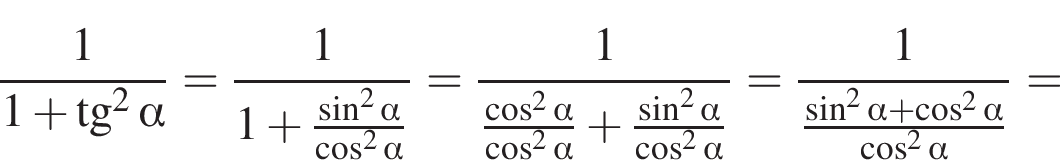
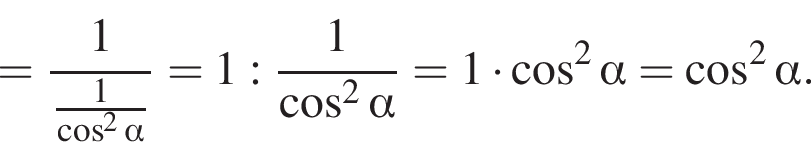
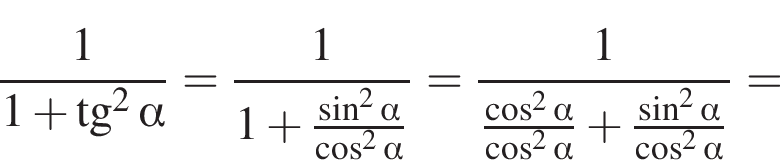
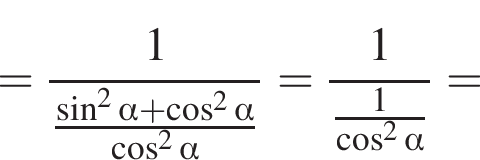
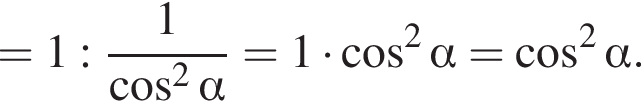
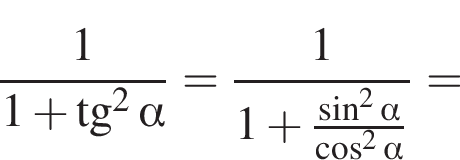
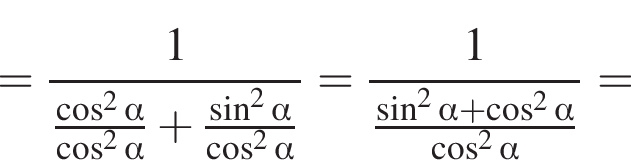
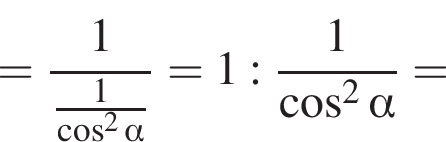
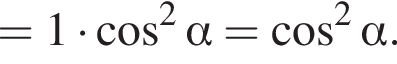
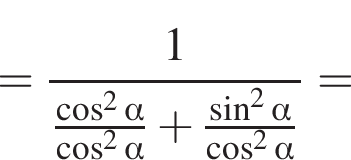
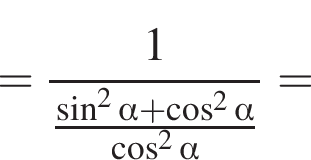
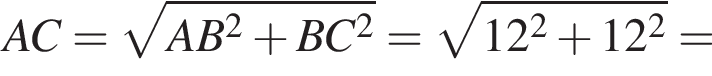
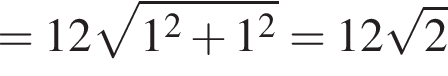
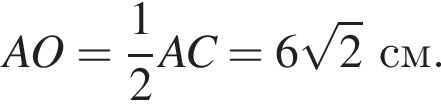
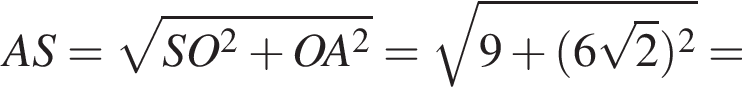
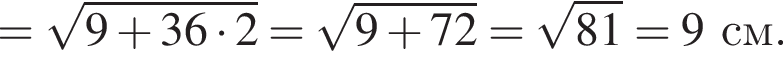
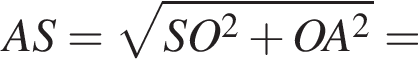
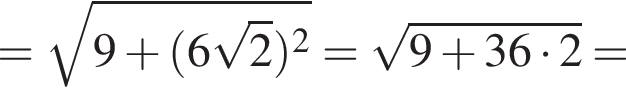
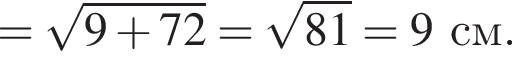
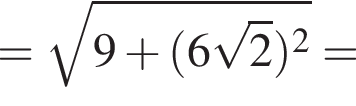
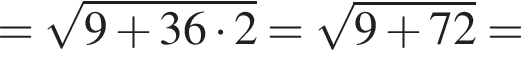
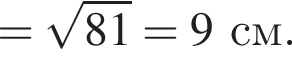
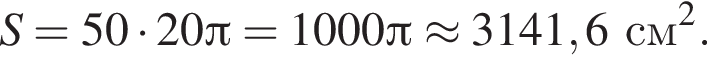
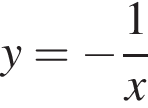 при положительных x принимает отрицательные значения, то есть ее график не проходит через первую четверть. Такой вариант остался один (А).
при положительных x принимает отрицательные значения, то есть ее график не проходит через первую четверть. Такой вариант остался один (А). 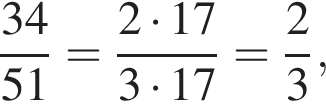 у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.
у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.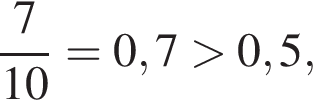
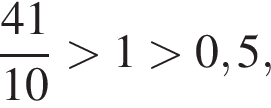
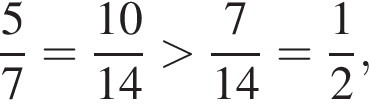
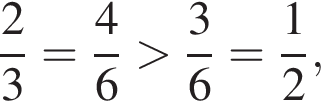
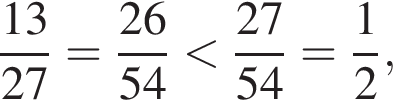
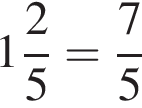 будет дробь
будет дробь 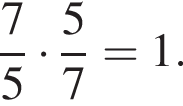
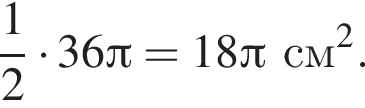
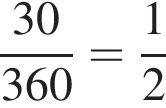 часть площади круга радиуса 12, то есть
часть площади круга радиуса 12, то есть 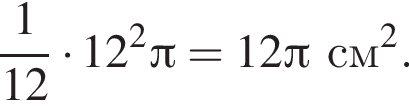
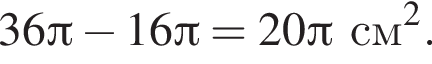
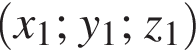 и
и 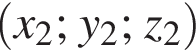 вычисляется по формуле
вычисляется по формуле 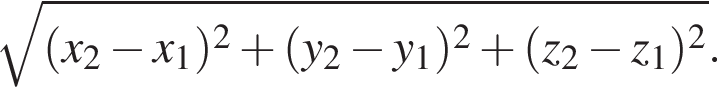 Значит
Значит 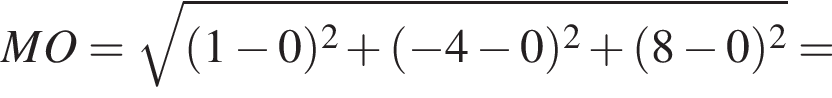
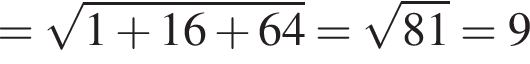
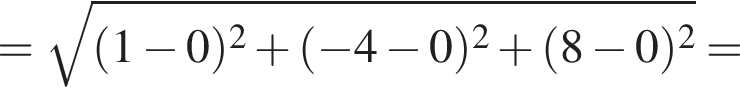
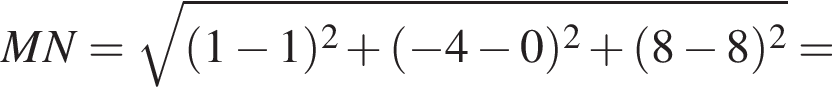
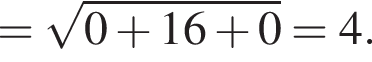
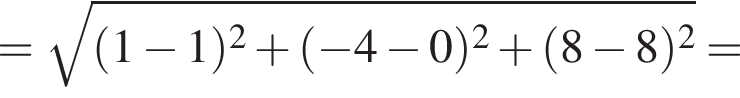
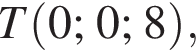 так как координата z не меняется, а остальные заменяются на нули, тогда расстояние от M до оси OZ равно
так как координата z не меняется, а остальные заменяются на нули, тогда расстояние от M до оси OZ равно 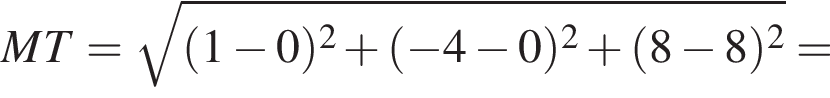
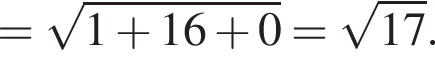
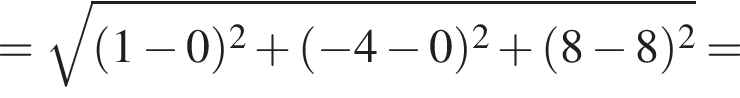
 По условию
По условию  откуда
откуда 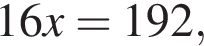
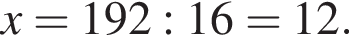
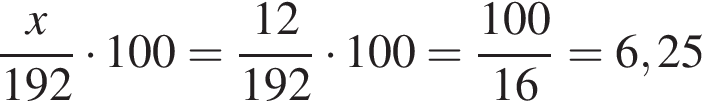
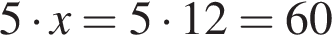 штук.
штук.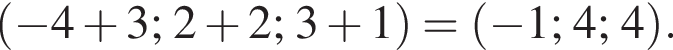
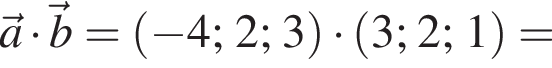
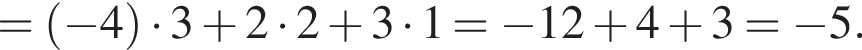
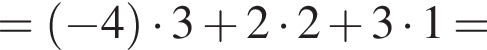
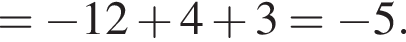
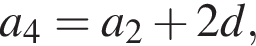 откуда
откуда 
 также
также 
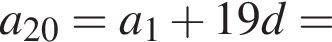

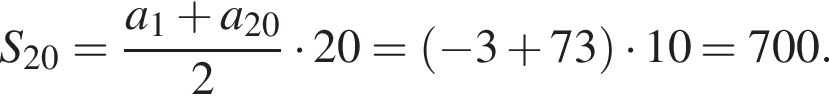
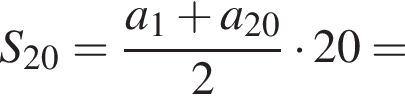
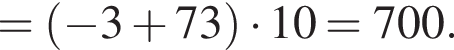
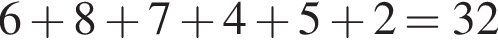 работы, из которых 4 имеют оценку D, поэтому искомая вероятность равна
работы, из которых 4 имеют оценку D, поэтому искомая вероятность равна 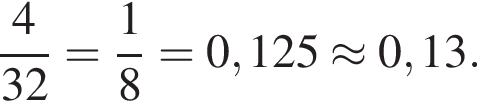
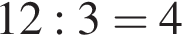 километра в час, а по течению
километра в час, а по течению  километра в час. Разность этих скоростей — удвоенная скорость течения, поэтому скорость течения равна
километра в час. Разность этих скоростей — удвоенная скорость течения, поэтому скорость течения равна 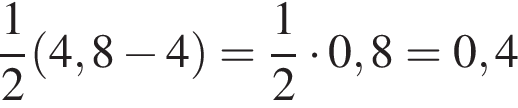
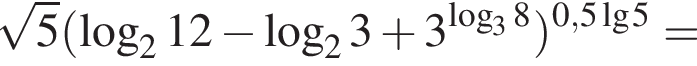
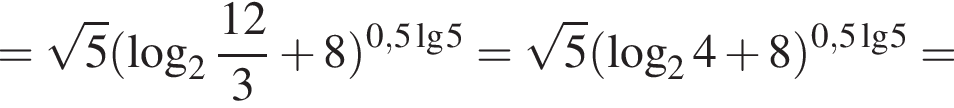
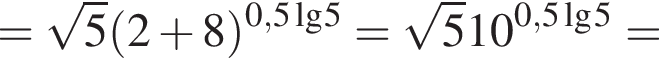
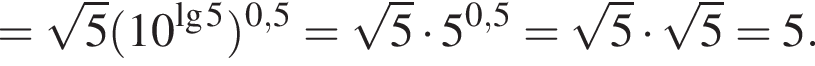
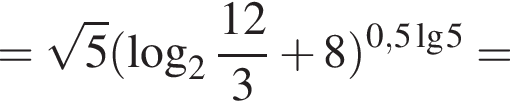
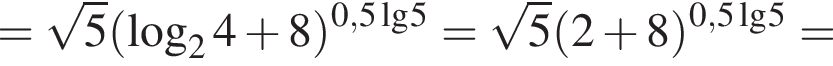
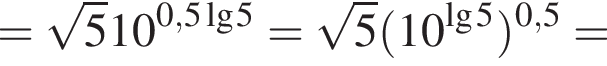

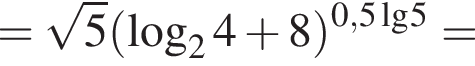
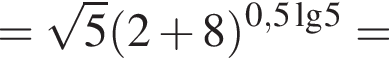
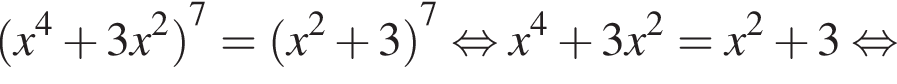
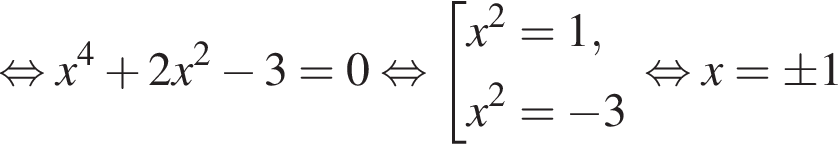
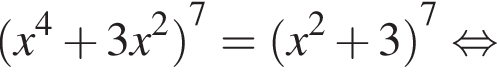

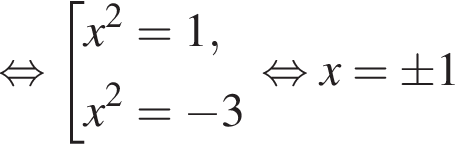
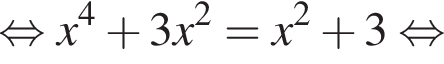
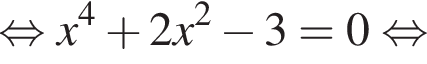
 способами. Совмещая каждый способ из первого набора с каждым способом из второго, получим
способами. Совмещая каждый способ из первого набора с каждым способом из второго, получим 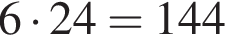 способа.
способа.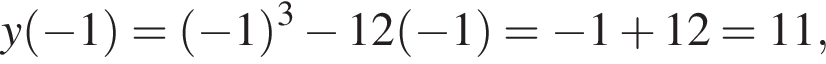
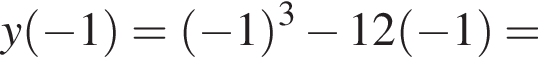
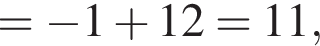
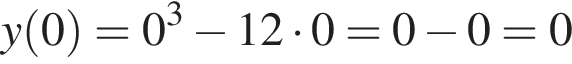
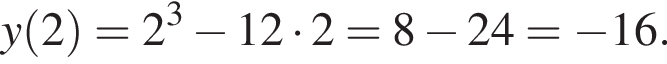
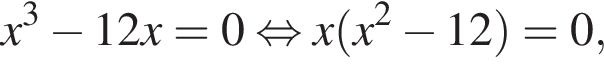 откуда
откуда 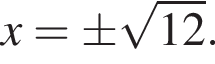 Возьмем производную:
Возьмем производную: 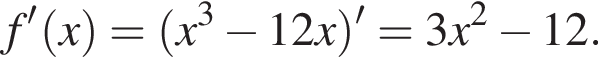 Решая уравнение
Решая уравнение 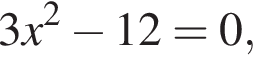 получим
получим 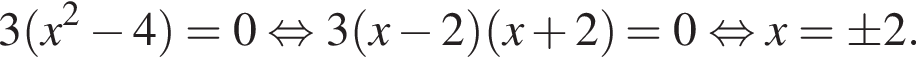
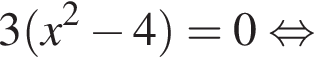
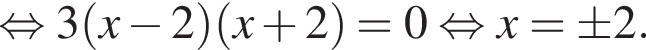
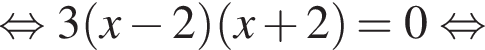

 и при
и при  (функция убывает). При
(функция убывает). При 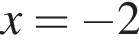 у функции максимум,
у функции максимум, 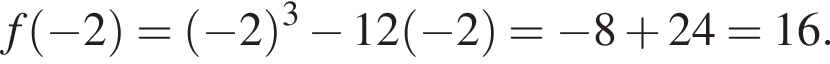
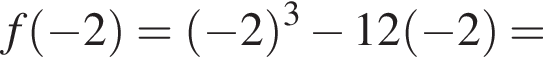
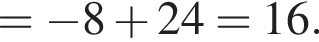
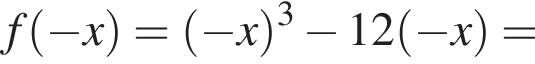
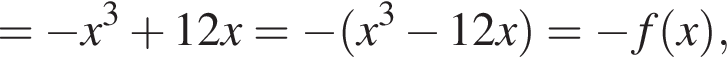
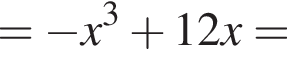
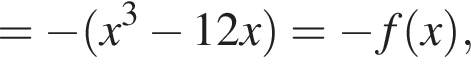
 поэтому
поэтому 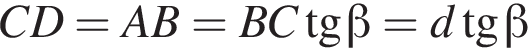
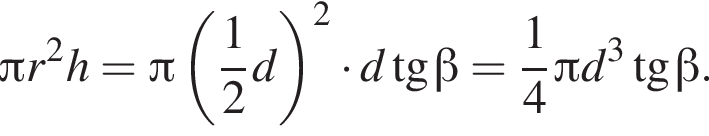
 а
а  поскольку опирается на диаметр, то
поскольку опирается на диаметр, то 
 Значит,
Значит, 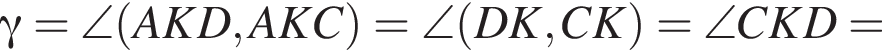
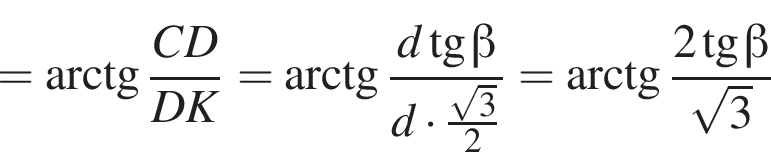

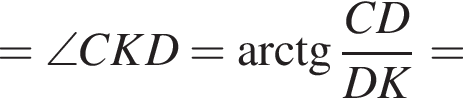
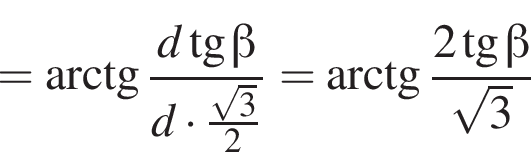

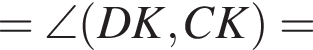
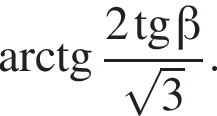

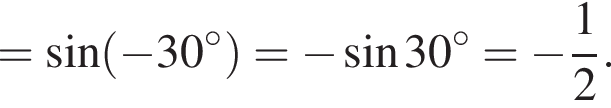
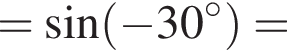
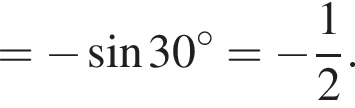
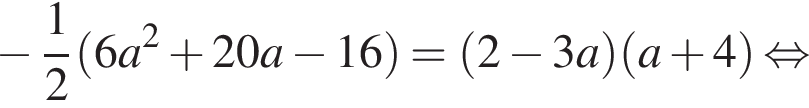

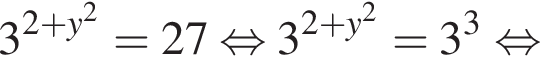
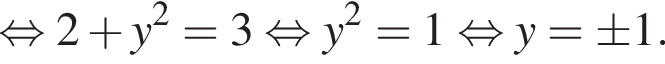
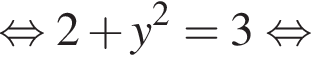

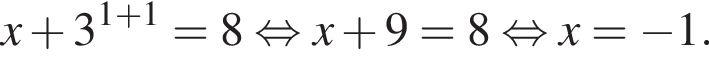 Итак,
Итак, 
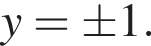 Теперь решим систему при прочих значениях a. Второе уравнение можно переписать в виде
Теперь решим систему при прочих значениях a. Второе уравнение можно переписать в виде 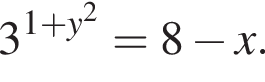 Сразу отметим, что
Сразу отметим, что  поэтому
поэтому 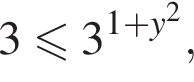 также
также 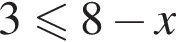 и
и 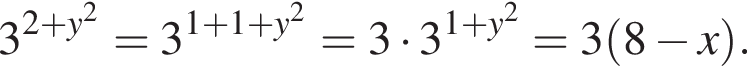
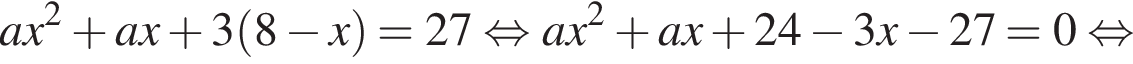

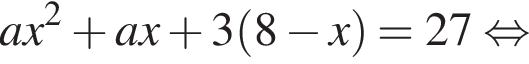
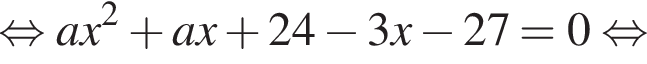
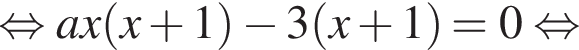
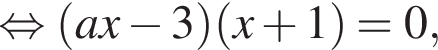
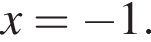 Если
Если 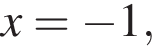 то
то 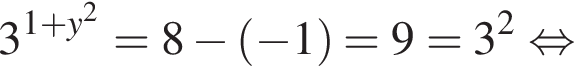
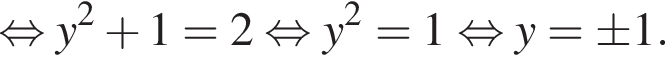
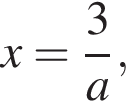 причем
причем 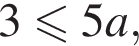 то есть
то есть 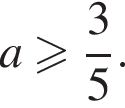 При таких a получаем
При таких a получаем 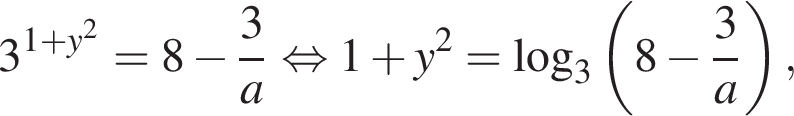
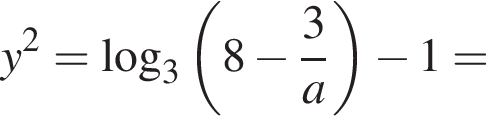
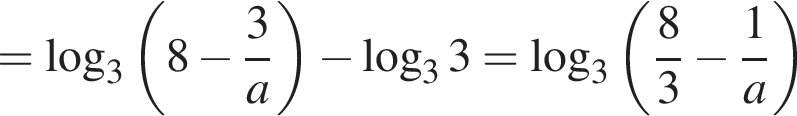
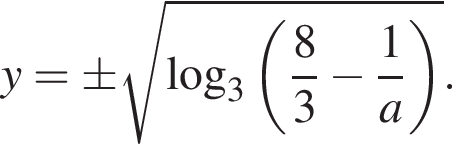
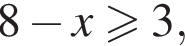 о котором мы позаботились. Есть два отдельных случая. Если
о котором мы позаботились. Есть два отдельных случая. Если 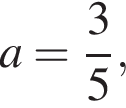 то
то 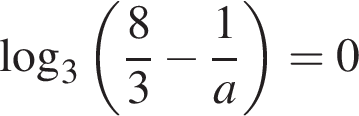 и
и 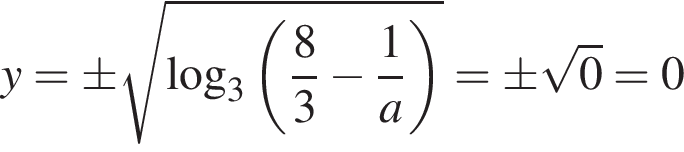 — то есть получается одно решение, а не два. Если
— то есть получается одно решение, а не два. Если 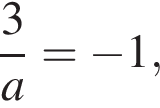 то есть
то есть 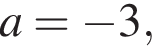 эти решения совпадают с уже найденными для
эти решения совпадают с уже найденными для 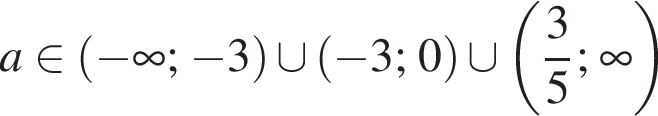 ответы
ответы 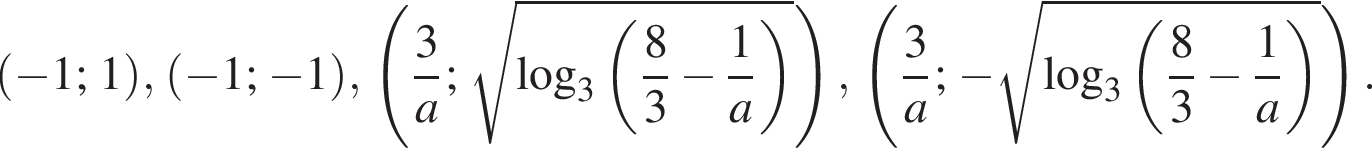 При
При 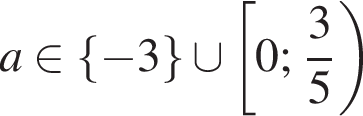 ответы
ответы 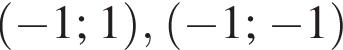 (случай
(случай