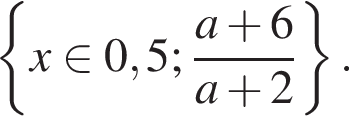На круговій діаграмі представлено інформацію з продажу 200 кг овочів протягом дня. Чому дорівнює маса (у кілограмах) проданої капусти?
За 12 хвилин велосипедист проїхав 4 кілометри. Скільки кілометрів він проїде за 33 хвилини, якщо їхатиме з тією ж швидкістю?
Основою прямої трикутної призми є прямокутний трикутник з катетами 6 і 8, бічне ребро дорівнює 5. Знайдіть об’єм призми.
Розв’яжіть рівняння 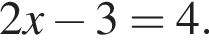
На діагоналі AC квадрата ABCD задано точку, відстань від якої до сторін AB і BC дорівнюе 2 cм і 6 см відповідно. Визначте периметр квадрата ABCD.
Функція
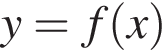 визначена й зростає на проміжку [−3: 2]. На рисунку зображено графік цієї функції на проміжку’ [−3; 0]. Яка з наведених точок може належати графіку' цієї функції?
визначена й зростає на проміжку [−3: 2]. На рисунку зображено графік цієї функції на проміжку’ [−3; 0]. Яка з наведених точок може належати графіку' цієї функції?
Спростити 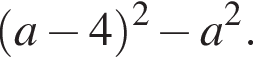
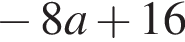

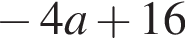
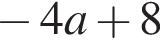
Радіус вписаного в прямокутний трикутник кола можна знайти за формулою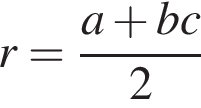 де a і b - катети, а c - гіпотенуза трикутника. Використовуючи цю формулу, знайдіть b , якщо
де a і b - катети, а c - гіпотенуза трикутника. Використовуючи цю формулу, знайдіть b , якщо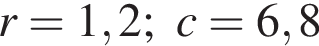 і
і![]() .
.
Спростіть вираз
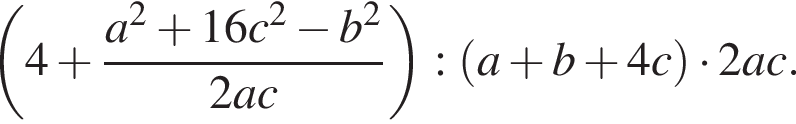
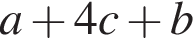
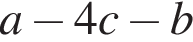
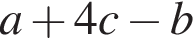
Які з наведених тверджень є правильними?
I.Через точку, що не лежить на даній прямій, можна провести єдину пряму, перпендикулярну даній прямій.
II. Через будь-які три точки проходить не більше однієї прямої.
III. Через будь-яку точку проходить більше однієї прямої.
Укажіть число, що є коренем рівняння 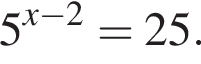
Використовуючи формулу Ньютона-Лейбніца, обчисліть 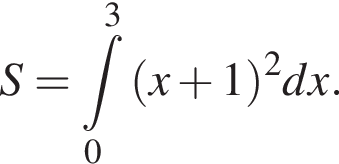
Розв’яжіть нерівність 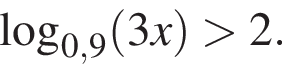
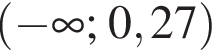
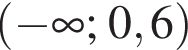
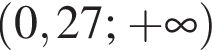
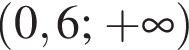
Знайдіть значення виразу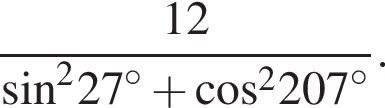
У прямокутнику відстань від точки перетину діагоналей до меншої сторони на 1 більша, ніж відстань від неї до більшої сторони. Периметр прямокутника дорівнює 28. Знайдіть меншу сторону прямокутника.
Підлога кімнати має форму квадрата. На ній лежить квадратний килим, кожна сторона якого віддалена від найближчоїстіни кімнати на 20 см (див. рисунок). Визначте периметр килима, якщо периметр підлоги дорівнює 18 м. Н аявністю плінтусів на підлозі знехтуйте.
Увідповідніть функцію (1-3) та її властивості (А-Д):
1 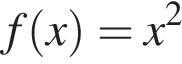
2 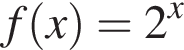
3 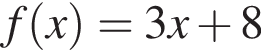
А графік функції проходить через точку з координатами (0;1)
Б функція спадає на всій області визначення
В функция является периодической
Г графіком функції є пряма
Д функція спадає на проміжку 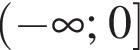
Установіть відповідність між виразом (1–3) та проміжком (А–Д), якому належить його значення.
1 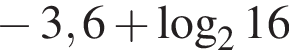
2 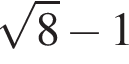
3 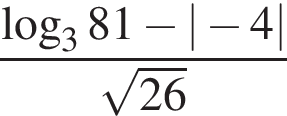
А ![]()
Б ![]()
В ![]()
Г 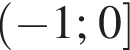
Д ![]()
У трикутнику АВС: АB = с, ВС = а, АС = b. До кожного початку речення (1−4) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Якщо a = b = c
2. Якщо 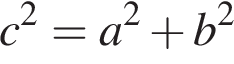
3. Якщо 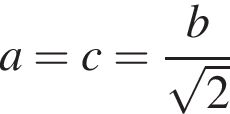
4. Якщо 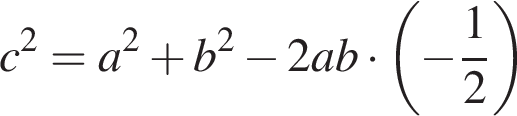
А то 
Б то 
В то 
Г то 
Д то 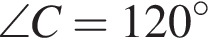
У циліндрі з центрами основ О і O1 проведено хорду АB в нижній основі (днв. рисунок).
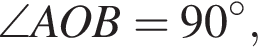
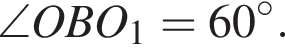 Площа основи циліндра дорівнює 9π. Установіть відповідність між величиною (1−4) та її значенням (А−Д).
Площа основи циліндра дорівнює 9π. Установіть відповідність між величиною (1−4) та її значенням (А−Д).
1. радiус основи цилiндра
2. довжина хорди AB
3. висота цилiндра
4. об'єм пiрамiди O1AOB
А ![]()
Б 3
В ![]()
Г ![]()
Д ![]()
Для поповнення рахунку телефону Андрій уніс певну суму грошей до платіжного термінала. З цієї суми утримано комісійний платіж у розмірі 2 грн 40 коп., що становить 3% від суми, унесеної до терміналу. У результаті рахунок телефону поповнено на решту внесеної суми.
1. Яку суму грошей (у гривня) Андрій уніс до платіжного термінала?
2. Мобільний оператор, послугам и якого користується Андрій, нараховує 8 бонусів за кожні 5 грн, на які поповнено рахунок телефону. На залишок грошей, менший за 5 грн, бонуси не нараховуються. Скільки бонусів нараховано Андрію за здійснене ним поповнення телефону?
На рисунку зображено прямокутник АВСD та півколо з центром О. Прямий AD — діаметр півкола

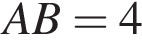 см.
см.
1. Визначте радіус півкола (у см).
2. Обчисліть площу трикутника KOM (у см2).
В прямоугольной системе координат в пространстве заданы точки A(−3; 1; −20) и C(5; 1; −6). Точка B — середина отрезка AC.
1. Найдите координаты B. В ответе укажите их сумму.
2. Найдите модуль вектора ![]() В ответе запишите квадрат найденного модуля.
В ответе запишите квадрат найденного модуля.
Геометрична прогресія задана умовою 
1. Укажите первый член этой прогрессии.
2. Знайдіть суму перших її 4 членів.
У коробці 8 синіх, 6 червоних та 11 зелених фломастерів. Випадковим чином обирають два фломастери. Яка ймовірність того, що оберуть один синій та один червоний фломастер?
За течією річки моторний човен проходить 32 км за 1 годину 20 хвилин, а проти течії — проходить 48 км за 3 години. Визначте власну швидкість човна (у км/год). Уважайте, що вона є сталою протягом усього руху.
Обчисліть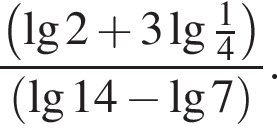
Розв’яжіть нерівність 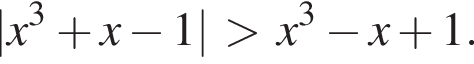 У відповіді запишіть суму всіх її цілих розв’язків на проміжку [−1; 5].
У відповіді запишіть суму всіх її цілих розв’язків на проміжку [−1; 5].
На колі розташовано 20 точок. Скільки є вписаних трикутників з вершинами у цих точках?
| x | y |
|---|---|
| 1 | |
| 2 | |
| 3 |
Вказано функцію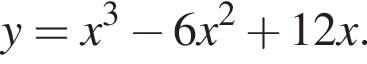
1. Для наведених у таблиці значень аргументів х визначте відповідні їм значення у (див. таблицю).
2. Знайдіть похідну f' функції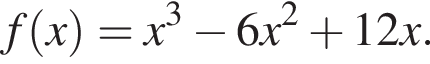
3. Напишіть рівняння прямої l , що дотикається графіка функції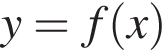 у його точці з абсцисою
у його точці з абсцисою
4. Визначте нулі функції f' .
5. Визначте проміжки зростання та спадання, точки екстремуму функції f .
6. Побудуйте графік функції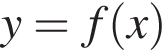 і пряму l .
і пряму l .
Апофема правильної чотирикутної піраміди дорівнює 2. Бічні ребра нахилені до основи під кутом α.
а) Зобразіть на малюнку цю піраміду та кут α.
б) Знайдіть кут нахилу бічних граней до основи.
в) Знайдіть площу поверхні піраміди.
Відповідно до умови завдання 31 (№ 3478) сторона основи правильної трикутної піраміди дорівнює 2. Бічні ребра нахилені до основи під кутом α.
1. Зобразіть на малюнку цю піраміду і збудуйте лінійний кут двогранного кута при основі.
2. Знайдіть цей кут.
Доведіть тотожність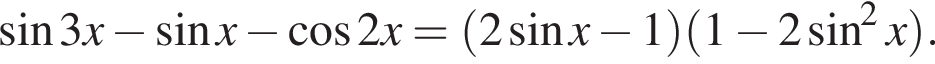
5. Задано рівняння 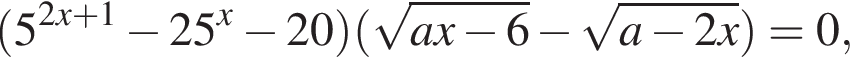 0, де х — змінна, а — стала.
0, де х — змінна, а — стала.
1. Розв’яжітьрівняння 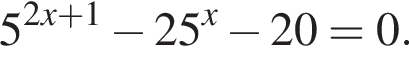
2. Розв’яжіть задане рівняння залежно від значень а.

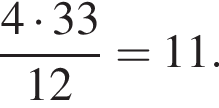
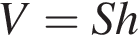 где S − площадь основания, а h − боковое ребро. Тогда объем равен
где S − площадь основания, а h − боковое ребро. Тогда объем равен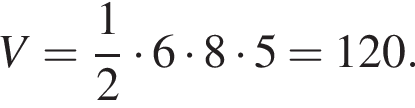
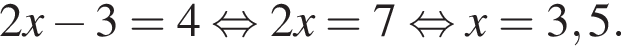
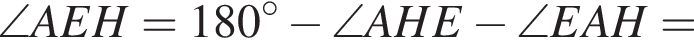
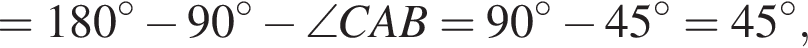
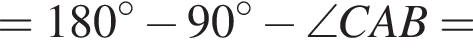

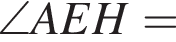

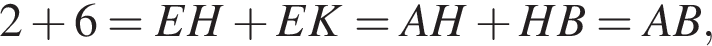
 см
см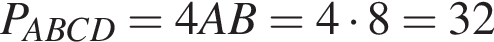 см.
см.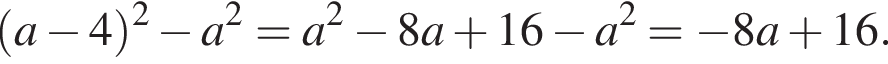
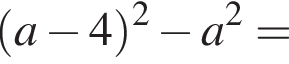
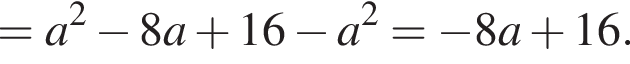
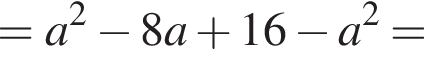
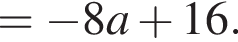
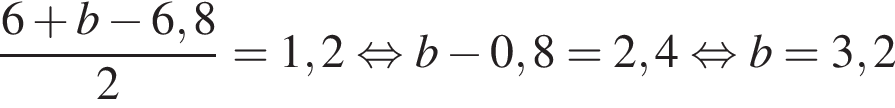
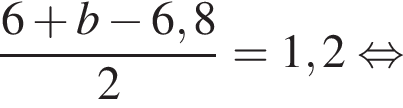
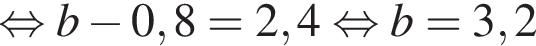
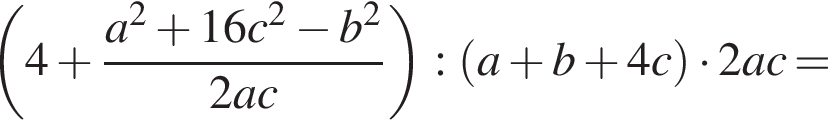
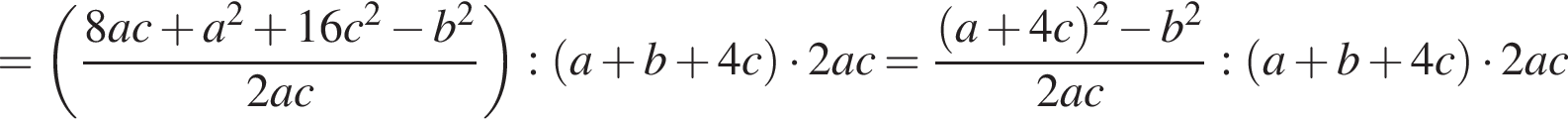
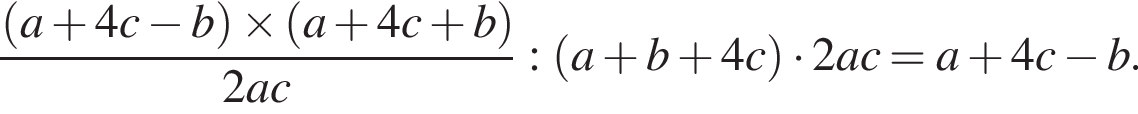
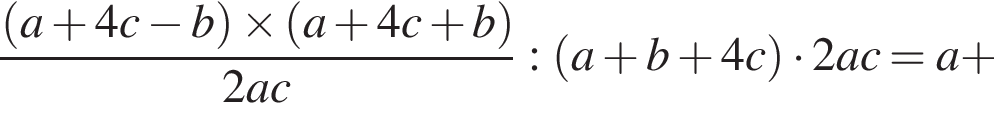
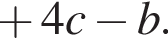
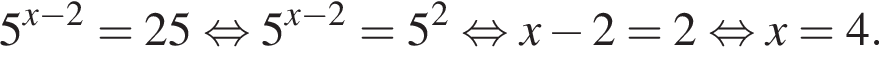
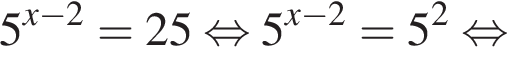

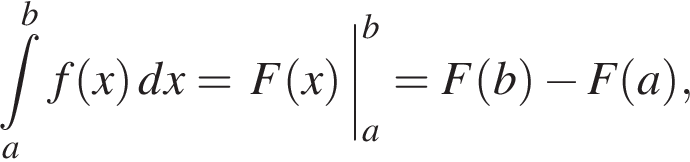
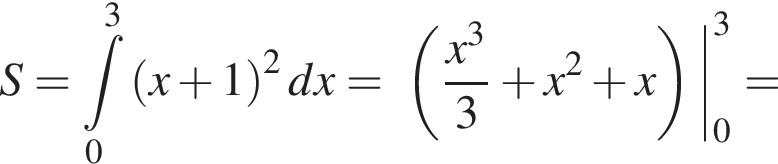
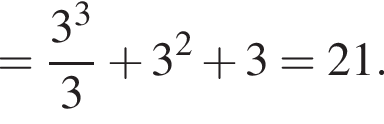
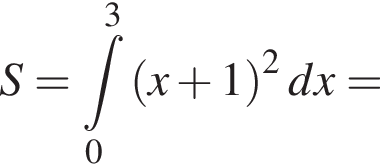
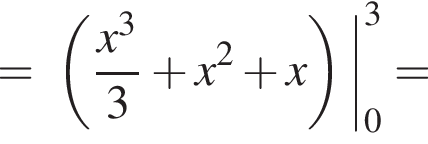
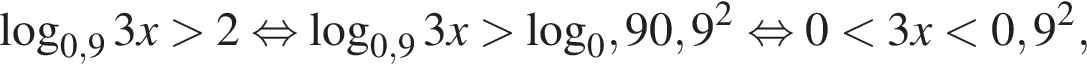
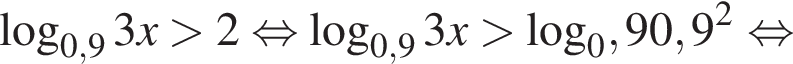
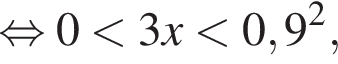
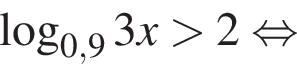
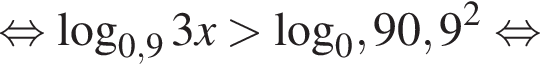
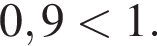 Итак,
Итак, 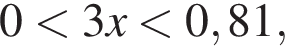 поэтому
поэтому 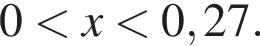
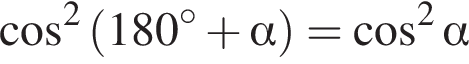 имеем:
имеем: 
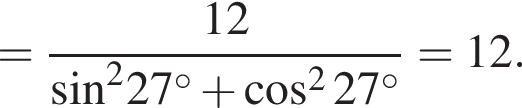
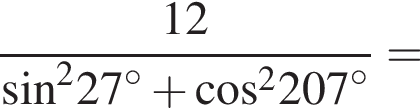
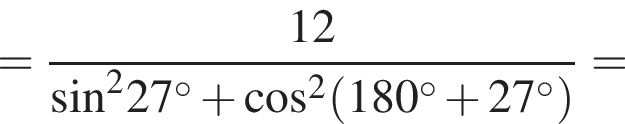
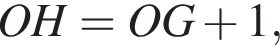 то
то 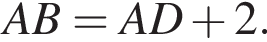 Тогда
Тогда

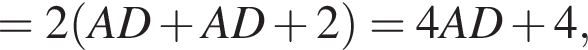
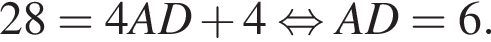
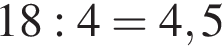 метров. Проведем отрезок, содержащий край ковра, от одного края комнаты до другого. Его длина будет
метров. Проведем отрезок, содержащий край ковра, от одного края комнаты до другого. Его длина будет 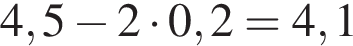 метра. Тогда периметр ковра равен
метра. Тогда периметр ковра равен 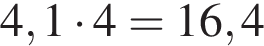 метра.
метра.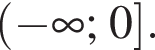 Ответ — Д.
Ответ — Д.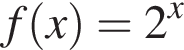 проходит через точку с координатами (0; 1). Ответ — А.
проходит через точку с координатами (0; 1). Ответ — А.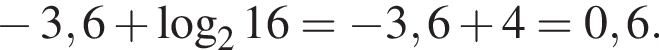 Данное значение соответствует промежутку
Данное значение соответствует промежутку 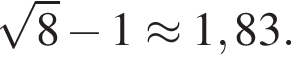 Данное значение соответствует промежутку
Данное значение соответствует промежутку 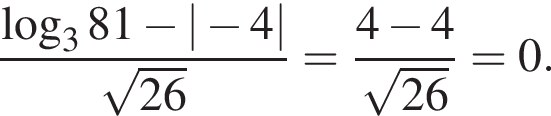 Данное значение соответствует промежутку
Данное значение соответствует промежутку 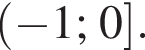 Ответ — Г.
Ответ — Г.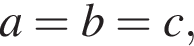 то треугольник ABC — равносторонний. Все углы равностороннего треугольника равны
то треугольник ABC — равносторонний. Все углы равностороннего треугольника равны  Получаем: 1 — В.
Получаем: 1 — В. 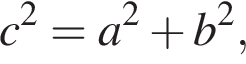 то по следствию из теоремы косинусов треугольник ABC — прямоугольный. Следовательно 2 — Г.
то по следствию из теоремы косинусов треугольник ABC — прямоугольный. Следовательно 2 — Г.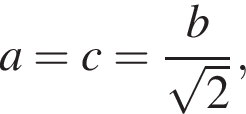 то треугольник ABC — равнобедренный, его боковые стороны — a и c, основание — b. В равнобедренном треугольнике высота является медианой, поэтому если CB = BA, а отрезки BH и AC перпендикулярны, получаем:
то треугольник ABC — равнобедренный, его боковые стороны — a и c, основание — b. В равнобедренном треугольнике высота является медианой, поэтому если CB = BA, а отрезки BH и AC перпендикулярны, получаем: 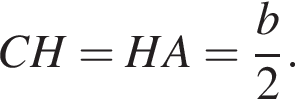 Треугольник BHC — прямоугольный,
Треугольник BHC — прямоугольный, 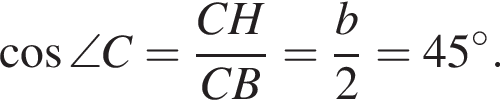
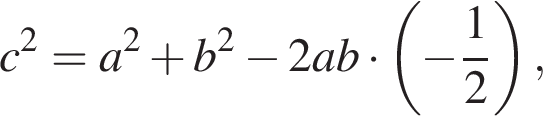
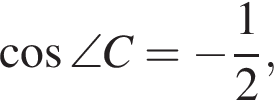 звідки
звідки  Итак, 4 — Д.
Итак, 4 — Д.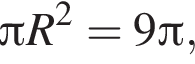
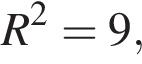
 как радиусы окружности, поэтому треугольник AOB — прямоугольный, а также равносторонний. Воспользуемся теоремой Пифагора:
как радиусы окружности, поэтому треугольник AOB — прямоугольный, а также равносторонний. Воспользуемся теоремой Пифагора: 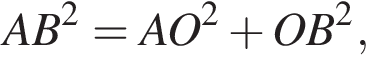 следовательно,
следовательно, 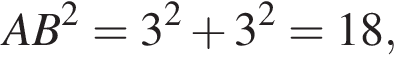 откуда
откуда 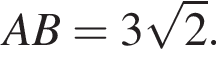 Таким образом, 2 — Г.
Таким образом, 2 — Г. получаем:
получаем: 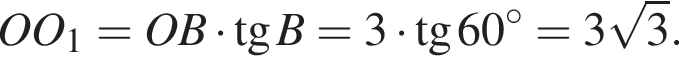
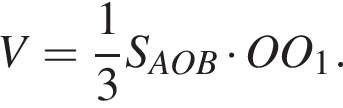 Сперва вычислим площадь треугольника AOB:
Сперва вычислим площадь треугольника AOB: 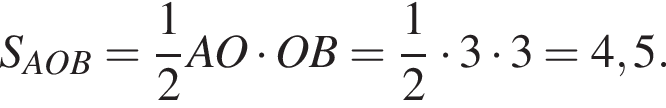
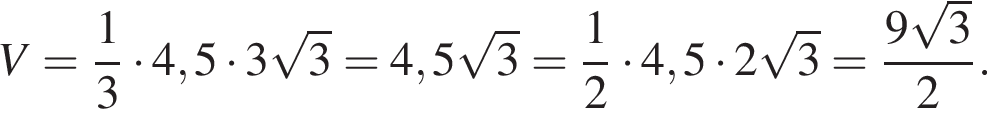
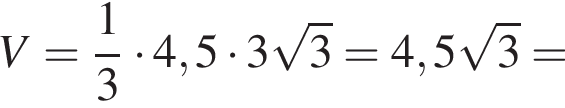
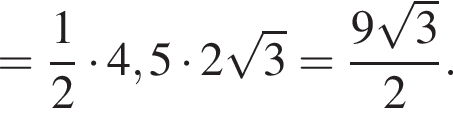
 гривен.
гривен.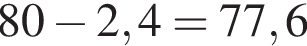 гривен,
гривен, бонусов.
бонусов.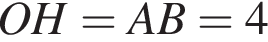 см
см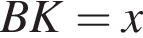 см
см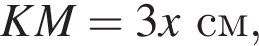
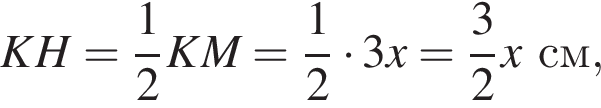
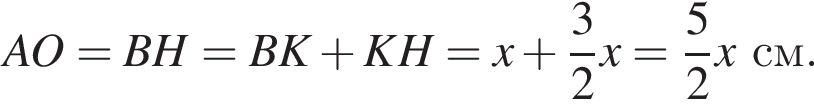

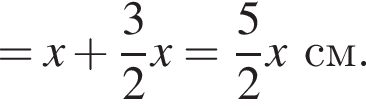
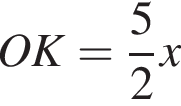 см
см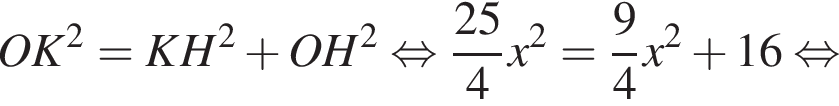
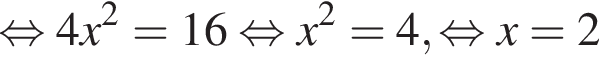
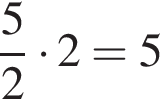 см
см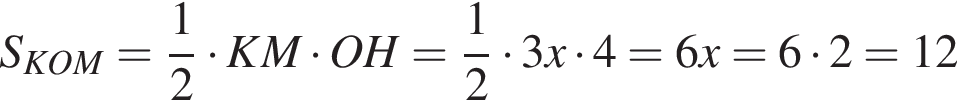
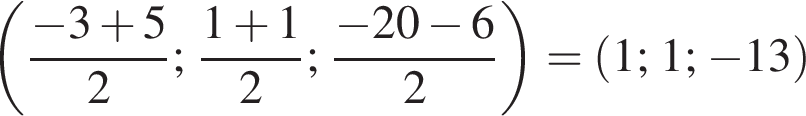

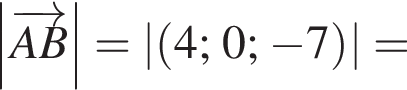
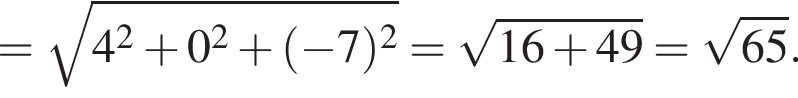
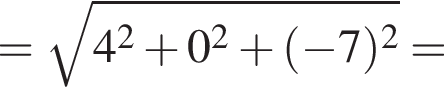
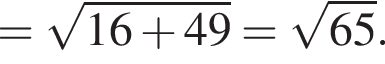
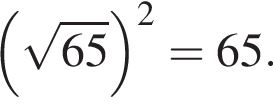
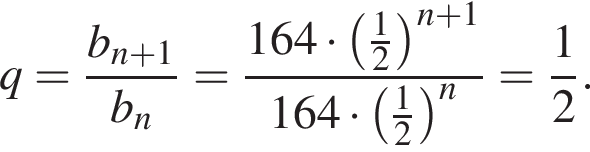
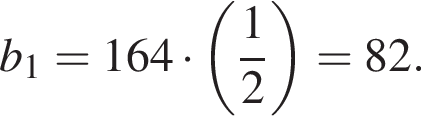 Сумма первых k членов геометрической прогрессии может быть найдена по формуле:
Сумма первых k членов геометрической прогрессии может быть найдена по формуле: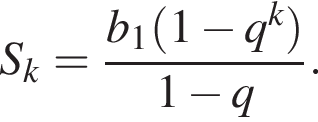
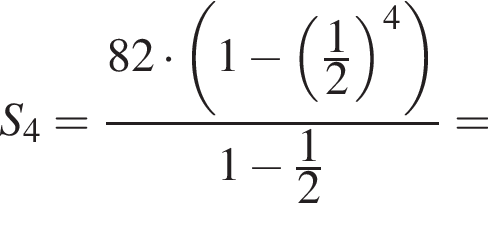
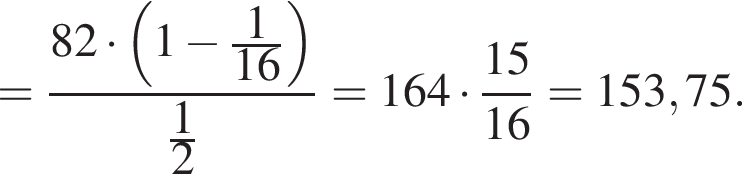
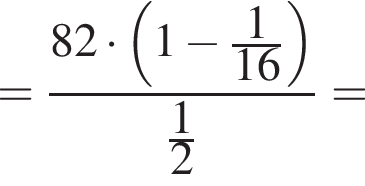
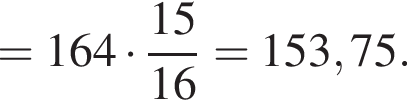
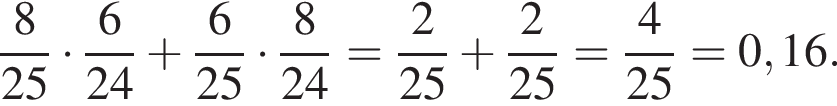
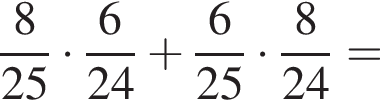
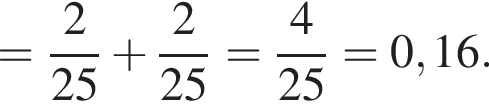
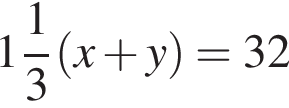 и
и 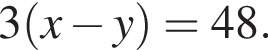
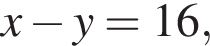
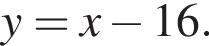 Подставляя в первое уравнение, получим
Подставляя в первое уравнение, получим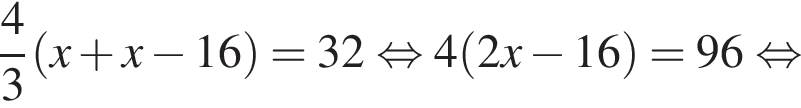

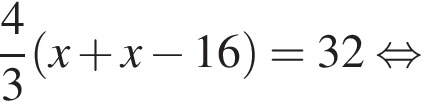
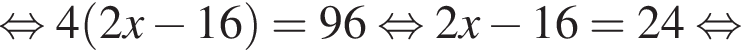
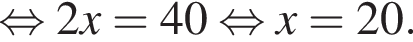
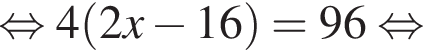
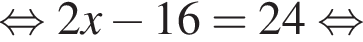
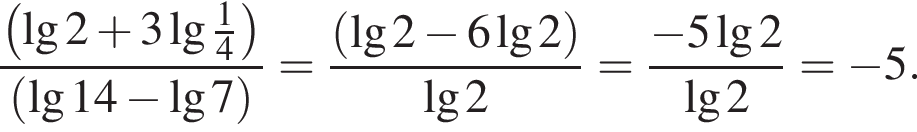
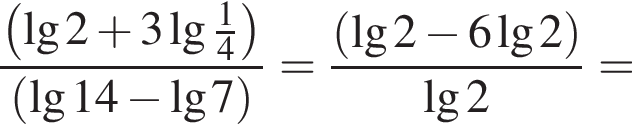
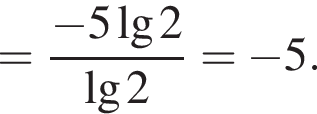
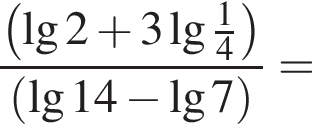
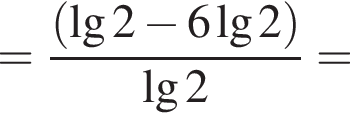
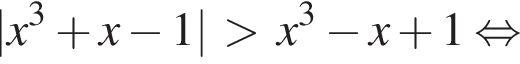
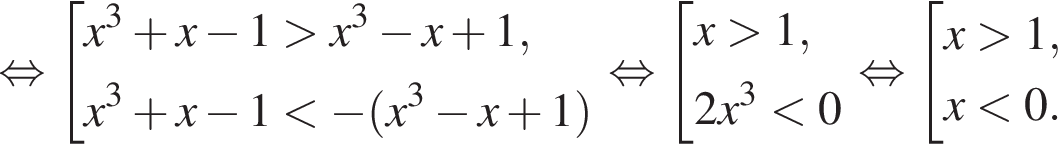
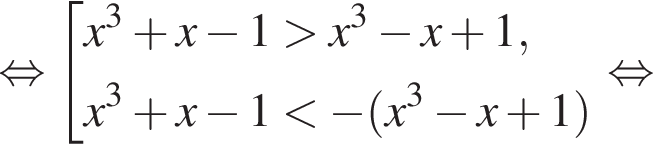
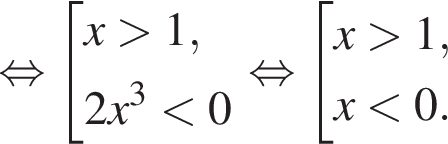
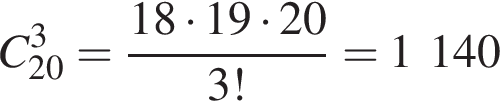 таких треугольников.
таких треугольников.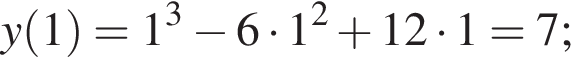
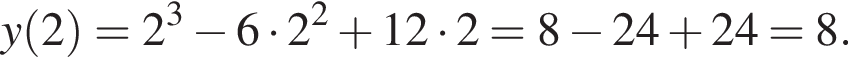
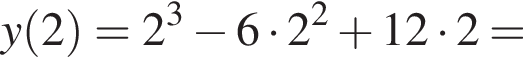

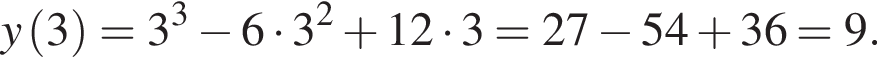
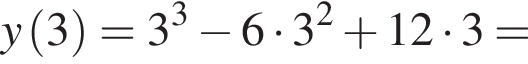
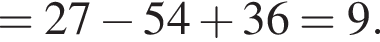
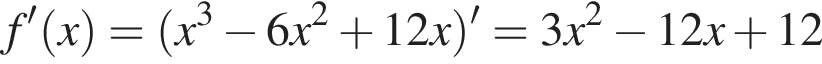
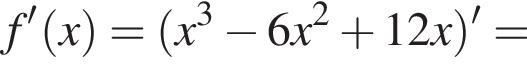
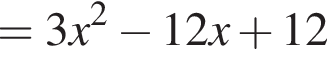
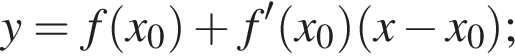
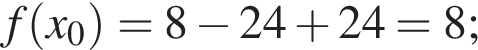
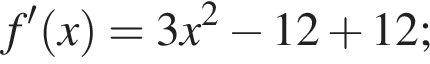
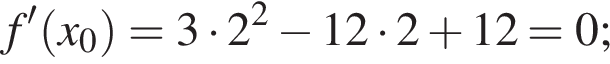
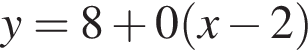 или
или 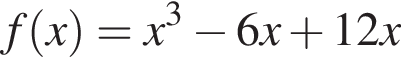 определена и дифференцируема на
определена и дифференцируема на 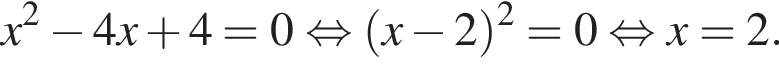
 На рисунке изображен график заданной функции
На рисунке изображен график заданной функции 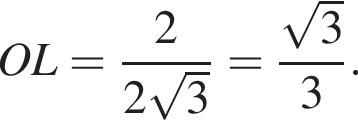 Выразим высоту SO пирамиды из прямоугольного треугольника SOL, получим:
Выразим высоту SO пирамиды из прямоугольного треугольника SOL, получим: 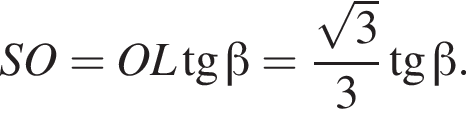
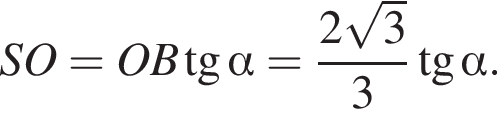
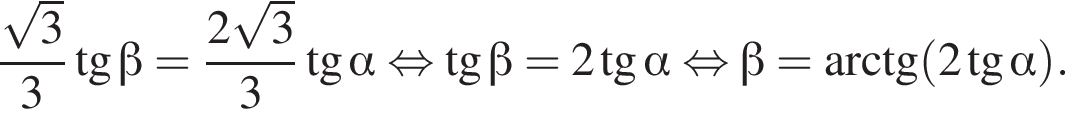
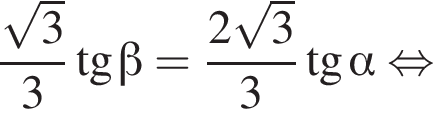

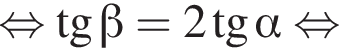


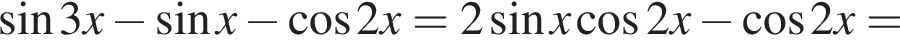
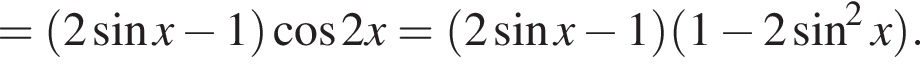
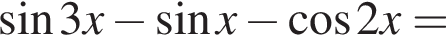
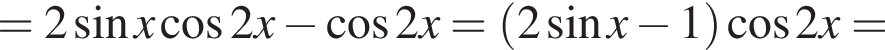
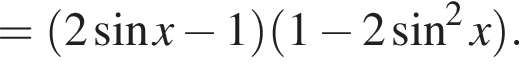
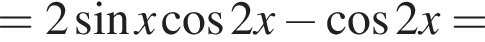
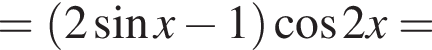

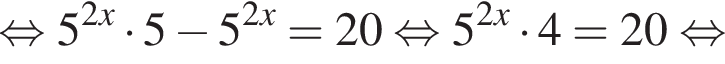
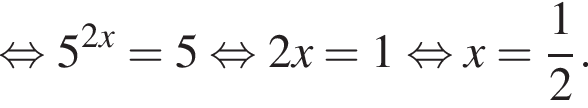
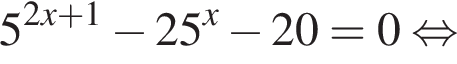
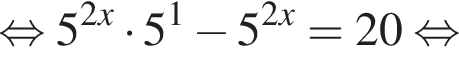
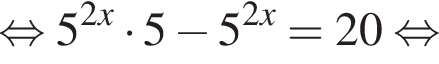
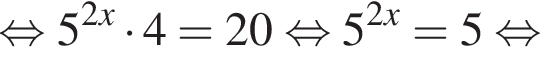
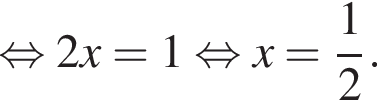


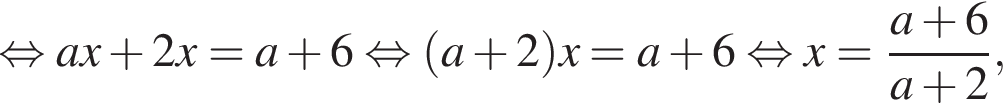


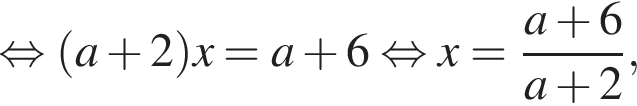

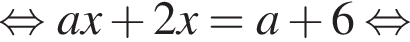
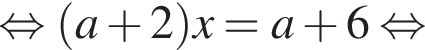
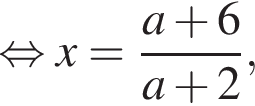
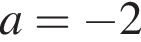 нет корней. Также нужно проверить, будет ли одно из подкоренных выражений неотрицательно, они равны друг другу для такого x, поэтому неотрицательность второго можно не проверять:
нет корней. Также нужно проверить, будет ли одно из подкоренных выражений неотрицательно, они равны друг другу для такого x, поэтому неотрицательность второго можно не проверять: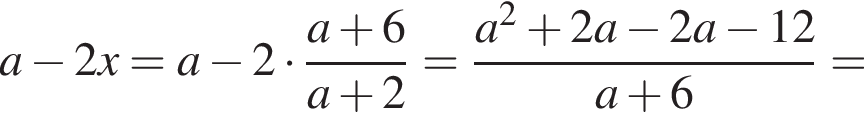
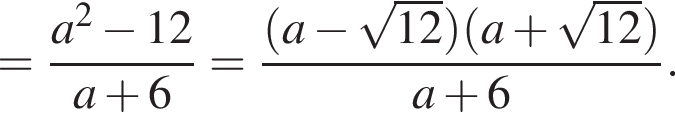
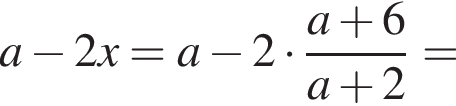
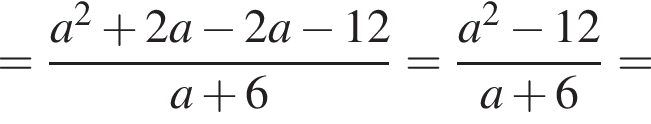
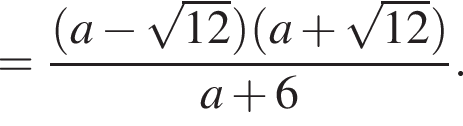
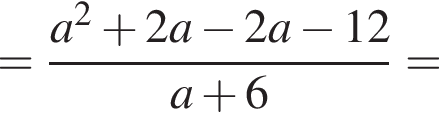
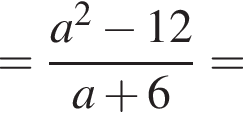
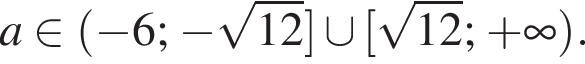 Теперь выясним, когда корнем будет
Теперь выясним, когда корнем будет 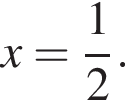 Для этого должны быть неотрицательны оба подкоренных выражения, то есть
Для этого должны быть неотрицательны оба подкоренных выражения, то есть 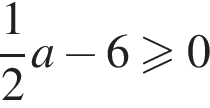 и
и 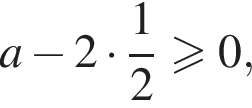 откуда
откуда 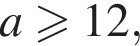 второе дает
второе дает 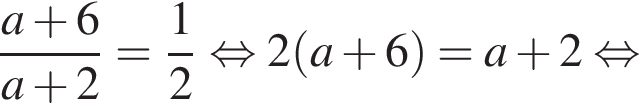

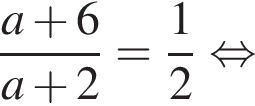



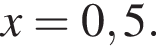
 то рівняння коренів не має;
то рівняння коренів не має; 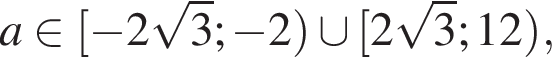 то
то 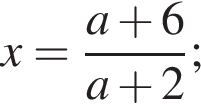
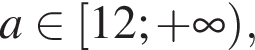 то
то