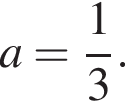На рисунку жирними точками позначено річні мінімуми площі поверхні арктичного льоду, що спостерігалися в період з 2004 р. по 2014 р. (для наочності точки з’єднано відрізками). По горизонталі відмічено роки, а по вертикалі — площу поверхні льоду (у млн км2). Користуючись наведеною інформацією, визначте із вказаного періоду рік, у якому величина річного мінімуму площі поверхні льоду змінилась найбільше порівняно з попереднім роком.
Спідометр автомобіля показує швидкість в милях на годину. Яку швидкість (в милях на годину) показує спідометр, якщо автомобіль рухається зі швидкістю 36 км на годину? (Вважайте, що 1 миля дорівнює 1,6 км.)
У циліндричний посуд налили 2000
![]() води. Рівень води при цьому досягає висоти 12 см. У рідину повністю занурили деталь. При цьому рівень рідини в посудині піднявся на 9 см. Чому дорівнює об’єм деталі? Відповідь висловіть у
води. Рівень води при цьому досягає висоти 12 см. У рідину повністю занурили деталь. При цьому рівень рідини в посудині піднявся на 9 см. Чому дорівнює об’єм деталі? Відповідь висловіть у ![]()
Розв’яжіть рівняння: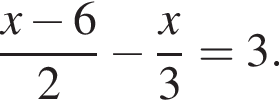
Знайдіть градусний захід кута, суміжного з кутом, радіальний захід якого дорівнює![]() .
.
На рисунку зображено графік функції
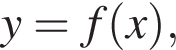 визначеної на проміжку [−2; 4]. Цей графік перетинає вісь y в одній із зазначених точок. Укажіть цю точку.
визначеної на проміжку [−2; 4]. Цей графік перетинає вісь y в одній із зазначених точок. Укажіть цю точку.
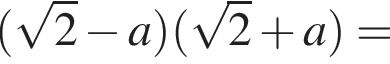
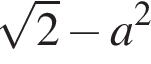
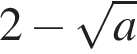
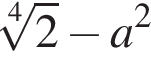
Площу чотирикутника можна обчислити за формулою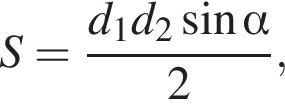 де
де![]() і
і![]() - Довжини діагоналей чотирикутника,
- Довжини діагоналей чотирикутника,![]() - Кут між діагоналями. Використовуючи цю формулу, знайдіть довжину діагоналі
- Кут між діагоналями. Використовуючи цю формулу, знайдіть довжину діагоналі![]() якщо
якщо
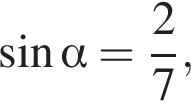 a
a![]()
Укажіть вираз, тотожно рівний виразу 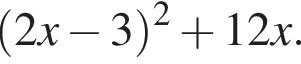
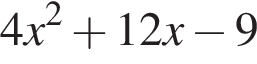
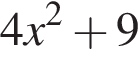
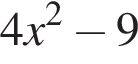
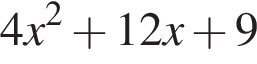
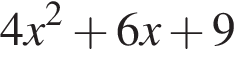
Які з наведених тверджень є правильними?
I. Через будь-які три точки проходить тільки одна пряма.
II. Відрізок, що з'єднує середини діагоналей трапеції, дорівнює напіврізниці її основ.
III. Вписані кути, що спираються на одну й ту саму хорду кола, рівні.
Розв’яжіть систему рівнянь
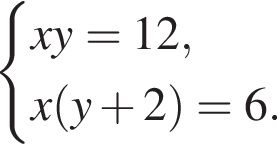
Використовуючи формулу Ньютона-Лейбніца, обчисліть 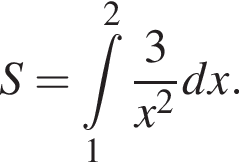
Розв'яжіть нерівність 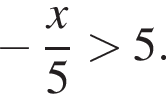
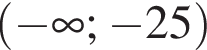
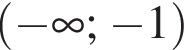
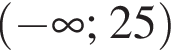
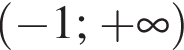
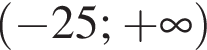
Спростіть вираз 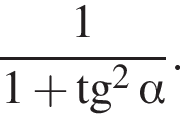
Знайдіть площу бічної поверхні правильної трикутної призми, описаної біля циліндра, радіус основи якого дорівнює
![]() а висота дорівнює 2.
а висота дорівнює 2.
Лист заліза, щоо має форму прямокутника ABCD
 згортають таким чином, щоб отримати циліндричну трубу (див. лівий і правий рисунки). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнюе 20 см. Виберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварювання знехтуйте.
згортають таким чином, щоб отримати циліндричну трубу (див. лівий і правий рисунки). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнюе 20 см. Виберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварювання знехтуйте.
Установіть відповідність між функцією (1−4) та її найбільшим значенням на проміжку [0; 5] (А−Д).
1. 
2. 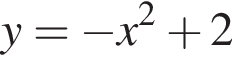
3. 
4. 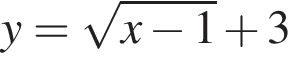
А 1
Б 2
В 3
Г 4
Д 5
Установіть відповідність між виразом (1−4) та твердженням про його значення (А−Д) при а= 15.
1. ![]()
2. ![]()
3. 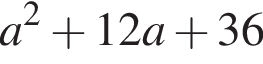
4. 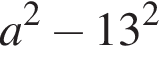
А менше за 20
Б є простим числом
В є парним
Г ділиться націло на 3
Д ділиться націло на 5
Установіть відповідність між геометричною фігурою (1−4) та її площею (А−Д).
1. круг радіуса 4 см (рис. 1)
2. півкруг радіуса 6 см (рис. 2)
3. сектор радіуса 12 см з градусною мірою центрального кута 30* (рис. 3)
4. кільце, обмежене колами радіусів 4 см і 6 см (рис. 4)
А 12π см2
Б 16π см2
В 18π см2
Г 20π см2
Д 24π см2
У прямокутній декартовій системі координат xyz у просторі задано точку М (1; −4; 8). Установіть відповідність між початком речення (1−4) та його закінченням (А−Д) так, щоб утворилося правильне твердження.
1. Відстань від точки M до площини ху дорівнює
2. Відстань від точки M до початку координат дорівнює
3. Відстань від точки M до осі z дорівнює
4. Відстань від точки M до N (1; 0; 8) дорівнює
А 1
Б 4
В ![]()
Г 8
Д 9
У магазині в продажу є лише музичні диски, диски з науково-популярними фільмами та диски з художніми фільмами. Кількість дисків із науково-популярними фільмами в п'ять разів більша за кількість музичних дисків і вдвічі менша за кількість дисків із художніми фільмами. Загальна кількість дисків у цьому магазині дорівнює 192.
1. Скільки відсотків становить кількість музичних дисків від загальної кількості всіх дисків у магазині?
2. Визначте кількість дисків із науково-популярними фільмами в цьому магазині.
У прямокутній трапеції АВСО проведено середню лінію MN (див. рисунок). Даний  см,
см,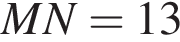 см
см
1. Визначте довжину сторони AD (у см).
2. Визначте довжину сторони AB (у см).
У прямокутній системі координат у просторі задано вектор 
1. Визначте координати вектора  У відповіді запишіть їхню суму.
У відповіді запишіть їхню суму.
2. Обчисліть скалярний добуток ![]()
Дано геометричну прогресію ( bn ), для якої b5 = −14, b8 = 112.
1. Знайдіть знаменник прогресії.
2. Укажите первый член прогрессии.
У чайному кіоску в наявності є лише розфасований у коробки по 100 г листовий чорний чай 7 видів, серед яких є вид «чорна перлина». Покупець вирішив придбати в цьому кіоску для подарункового набору три коробки чорного чаю трьох різних видів, серед яких обов’язково повинен бути вид «чорна перлина».
Скільки всього в покупця є варіантів такого придбання трьох коробок чаю для набору з наявних у кіоску?
Плавець під час першого тренування подолав дистанцію у 450 м. Кожного наступного тренування він пропливав на 50 м більше, ніж попереднього, поки не досягнув результату — 1000 м за одне тренування. Після цього під час кожного відвідування басейну плавець пропливав 1000 м.
Скільки всього кілометрів плавець проплив за перші 10 тижнів тренувань, якщо він тренувався тричі кожного тижня?
Обчисліть значення виразу
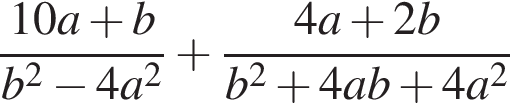
при 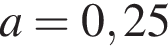 i
i 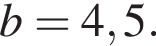
Розв'яжіть рівняння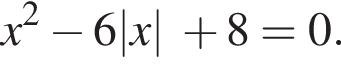 Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має кілька коренів, у відповідь запишіть їхню суму.
Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має кілька коренів, у відповідь запишіть їхню суму.
У магазині в наявності є 10 видів тортів та 15 видів пачок печива. Скільки всього є способів вибору в цьому магазині або одного торта, або трьох різних пачок печива для святкового вечора?
| x | y |
|---|---|
| −1 | |
| 0 | |
| 2 |
Задано функцію 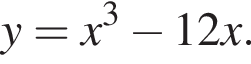
1. Для наведених у таблиці значень аргументи х визначте відповідні їм значення у (см. тблицу).
2. Визначте й запишіть координати точок перетину графіка функції 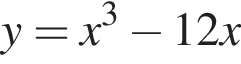 із віссю х.
із віссю х.
3. Знайдіть похідну f' функції 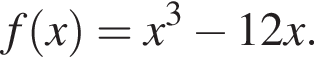
4. Визначте нулі функції f'.
5. Визначте проміжки зростання і спадання, точки екстремуму й екстремуми функції f.
6. Побудуйте ескіз графіка функції f.
Апофема правильної чотирикутної піраміди дорівнює 3. Бічні ребра нахилені до основи під
1. Зобразіть на малюнку цю піраміду та кут α.
2. Знайдіть кут нахилу бічних граней до основи.
3. Знайдіть площу поверхні піраміди.
Відповідно до умови завдання 31 (№ 3538) Апофема правильної чотирикутної піраміди дорівнює 3. Бічні ребра нахилені до основи під кутом α.
а) Зобразіть на малюнку цю піраміду та побудуйте двогранний кут при боковому ребрі.
б) Знайдіть цей кут.
Доведіть тотожність
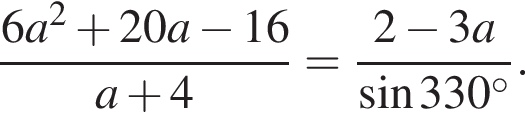
Розв’яжіть рівняння
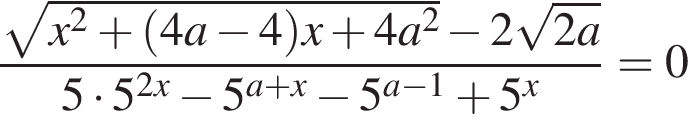
залежно від значень параметра a.

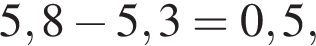 за 2007 —
за 2007 — 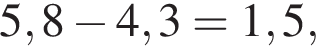 за 2009 —
за 2009 — 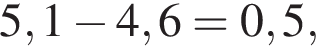 за 2012 —
за 2012 — 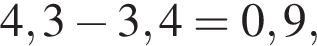 за 2013 —
за 2013 — 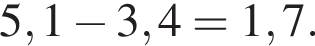 Это последнее и есть наибольшее.
Это последнее и есть наибольшее.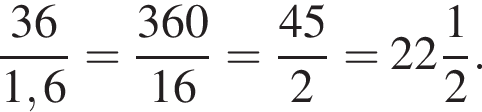
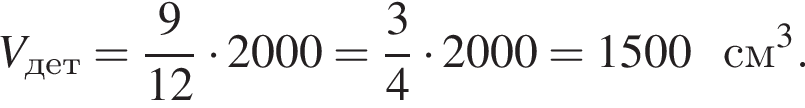
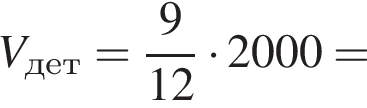
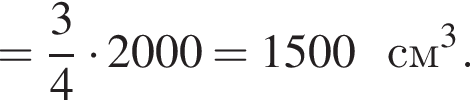
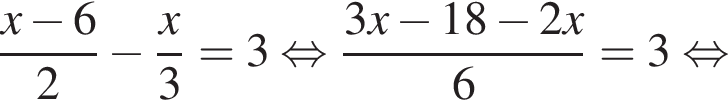
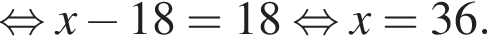
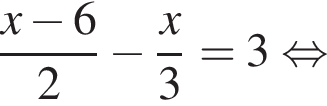
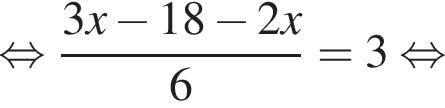
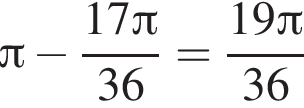 или 95°.
или 95°.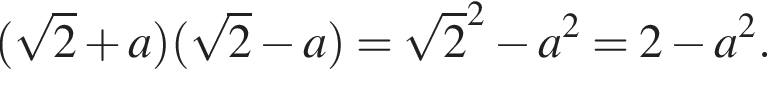
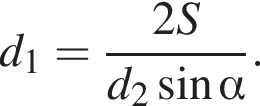
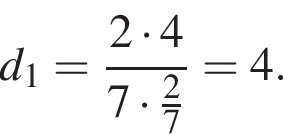
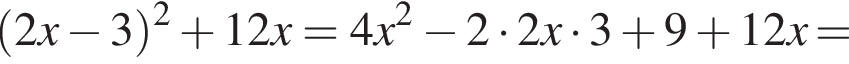
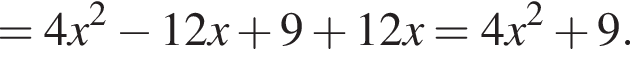
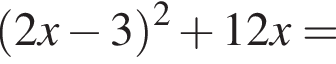
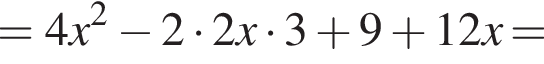
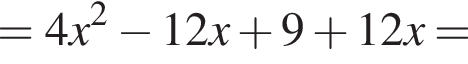
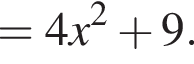
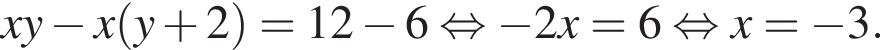
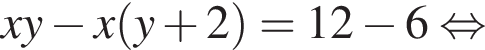
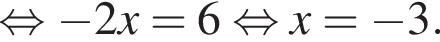
 в первое уравнение системы, получаем
в первое уравнение системы, получаем 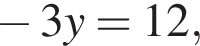
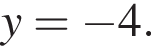 Значит,
Значит, 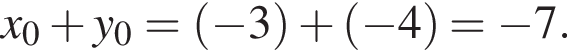
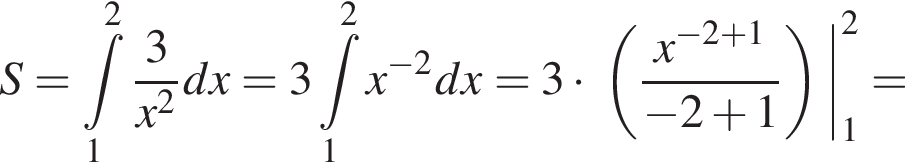
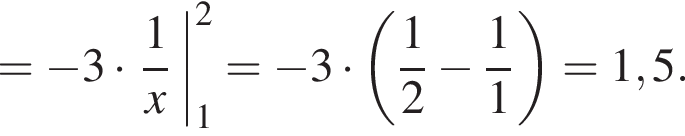
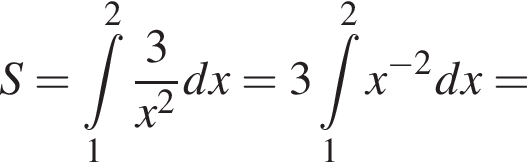

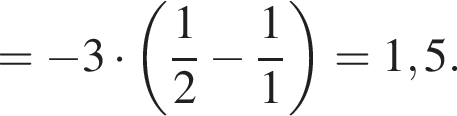
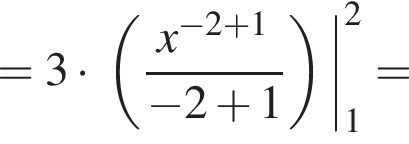
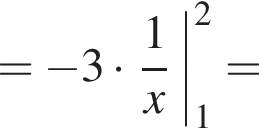
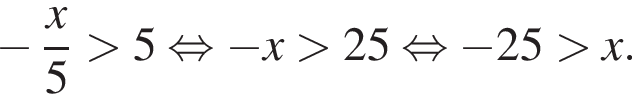
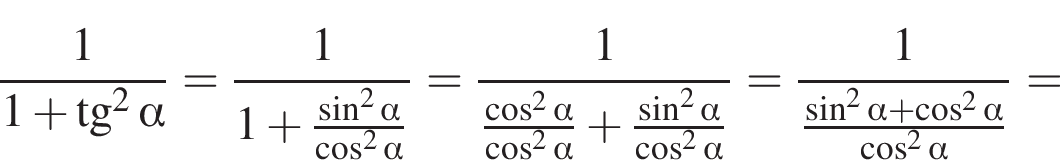
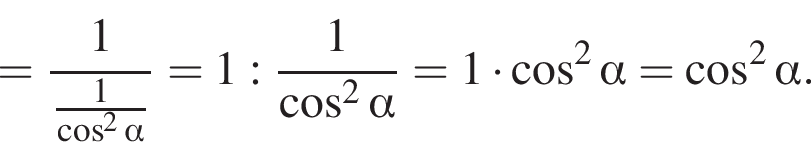
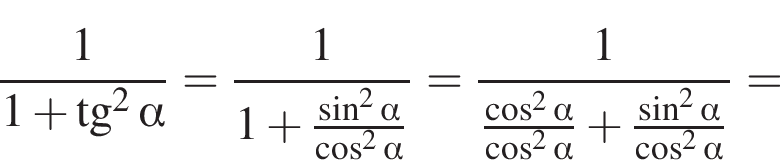
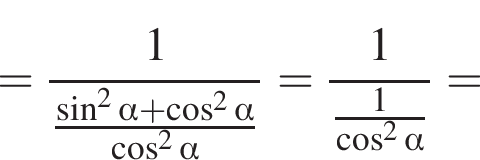
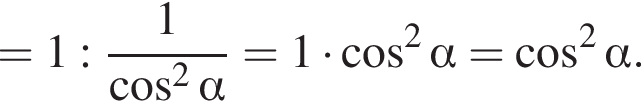
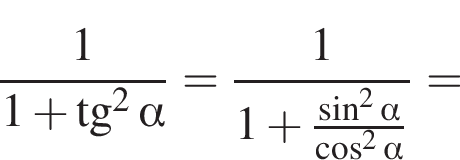
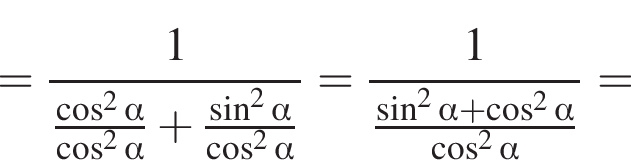
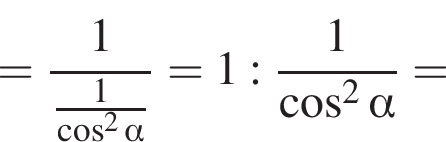
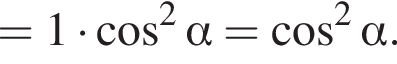
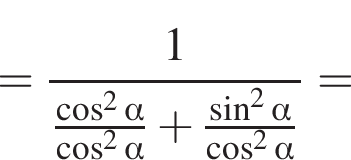
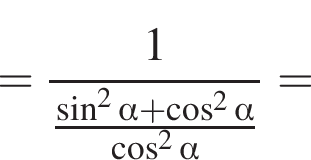
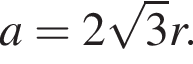 Тогда площадь боковой поверхности призмы выражается формулой
Тогда площадь боковой поверхности призмы выражается формулой 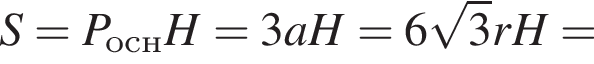
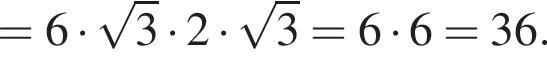
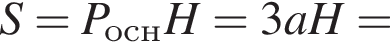
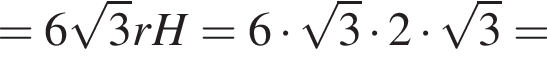

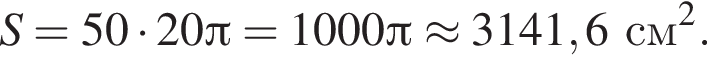
 возрастает, поэтому наибольшее значение на промежутке [0; 5] она принимает при наибольшем значении аргумента:
возрастает, поэтому наибольшее значение на промежутке [0; 5] она принимает при наибольшем значении аргумента: 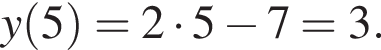 Таким образом, 1 —B.
Таким образом, 1 —B.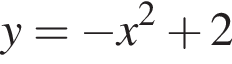 —
—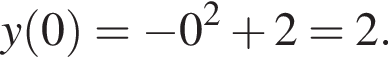 Таким образом, 2 — Б.
Таким образом, 2 — Б. 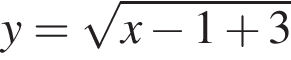 возрастает, поэтому при
возрастает, поэтому при 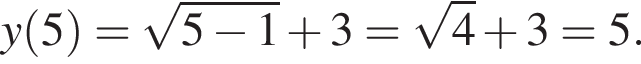
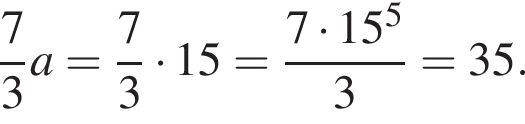
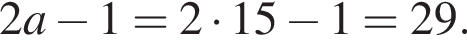 Полученное число является простым. Итак, 2 — Б.
Полученное число является простым. Итак, 2 — Б. 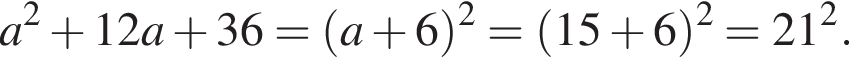
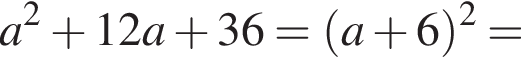
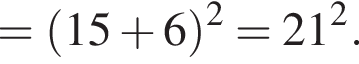
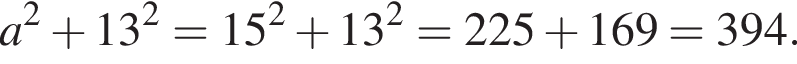
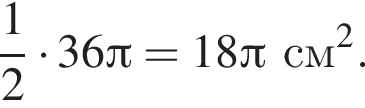
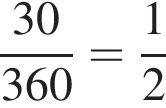 часть площади круга радиуса 12, то есть
часть площади круга радиуса 12, то есть 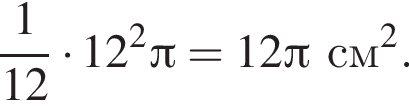
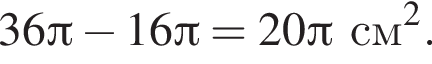
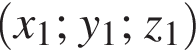 и
и 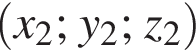 вычисляется по формуле
вычисляется по формуле 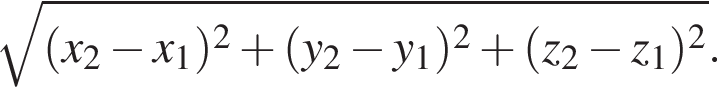 Значит
Значит 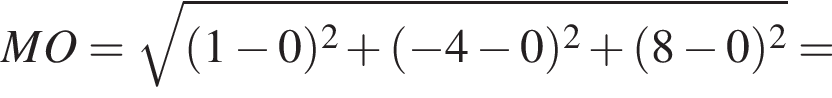
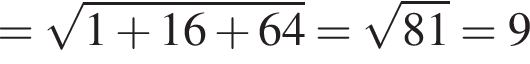
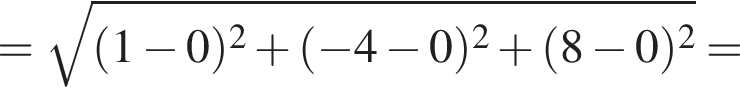
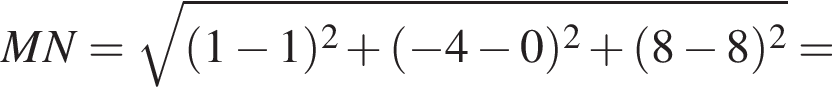
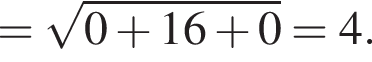
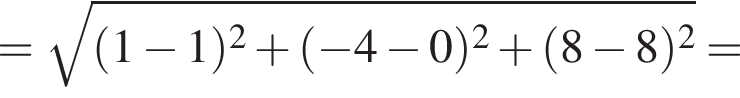
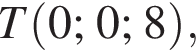 так как координата z не меняется, а остальные заменяются на нули, тогда расстояние от M до оси OZ равно
так как координата z не меняется, а остальные заменяются на нули, тогда расстояние от M до оси OZ равно 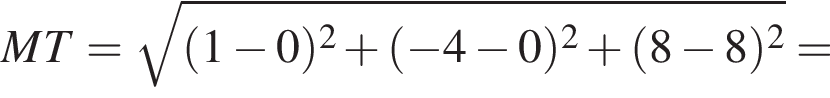
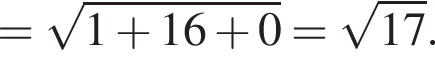
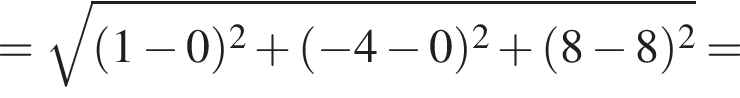
 По условию
По условию  откуда
откуда 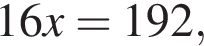
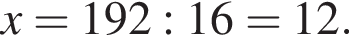
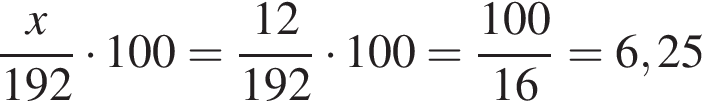
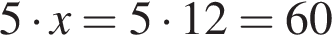 штук.
штук.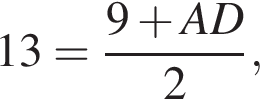 откуда
откуда 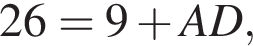
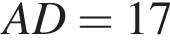 см. Опустим перпендикуляр CH на сторону AD. Тогда треугольник CHD — прямоугольный равнобедренный, так как
см. Опустим перпендикуляр CH на сторону AD. Тогда треугольник CHD — прямоугольный равнобедренный, так как 

 а ABCH — прямоугольник, значит
а ABCH — прямоугольник, значит 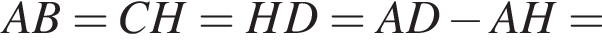
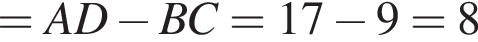
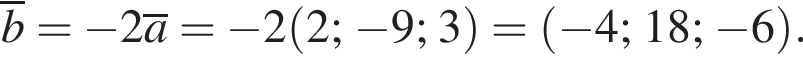
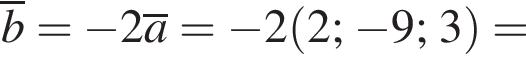
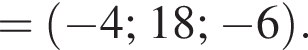
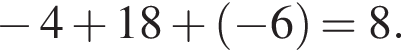 Найдем скалярное произведение векторов:
Найдем скалярное произведение векторов: 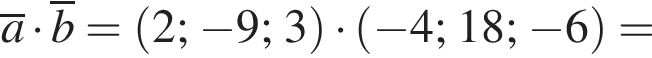
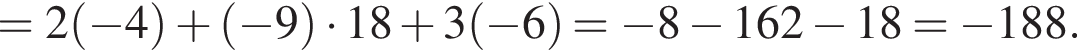



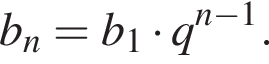 Зная, что b5 = −14 и b8 = 112, получаем систему уравнений. Решим систему, разделив второе уравнение на первое:
Зная, что b5 = −14 и b8 = 112, получаем систему уравнений. Решим систему, разделив второе уравнение на первое: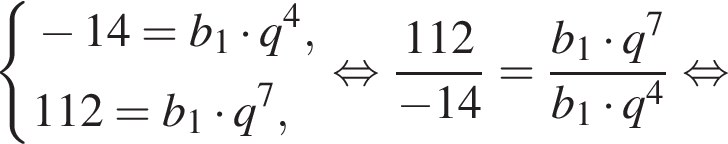
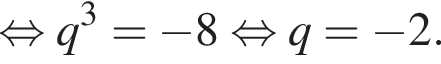
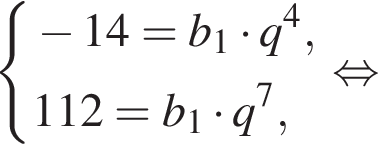
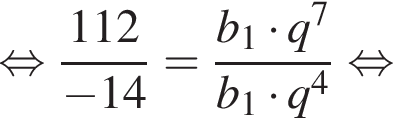
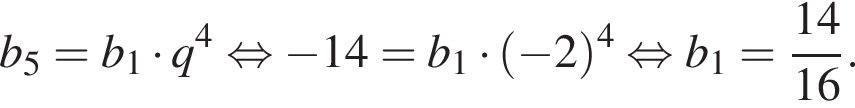
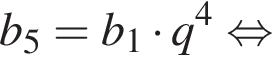
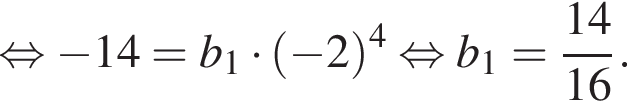
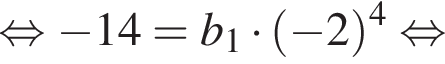
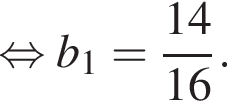
 вариантов. Однако здесь каждый вариант посчитан дважды, так как можно приобрести чай 3 и чай 5, а можно наоборот. Значит, правильный ответ —
вариантов. Однако здесь каждый вариант посчитан дважды, так как можно приобрести чай 3 и чай 5, а можно наоборот. Значит, правильный ответ — 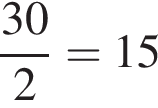 вариантов.
вариантов.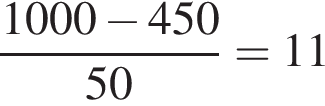 раз увеличивать расстояние. То есть на 12 тренировке он впервые проплывет 1000 метров. После этого он еще
раз увеличивать расстояние. То есть на 12 тренировке он впервые проплывет 1000 метров. После этого он еще 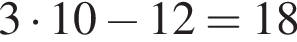 раз проплывет по 1000 метров. За первые же 12 тренировок он проплывет
раз проплывет по 1000 метров. За первые же 12 тренировок он проплывет 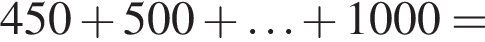
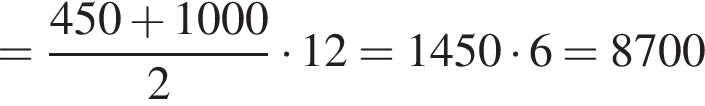
 метров, то есть
метров, то есть 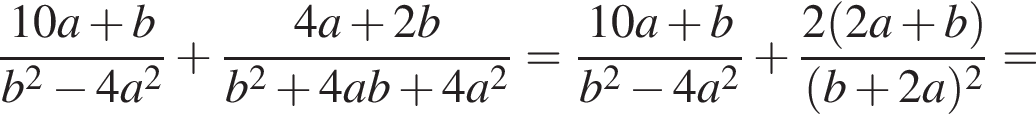
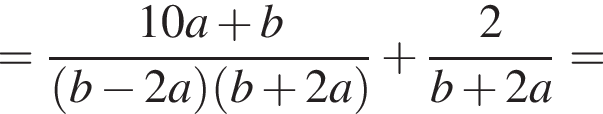
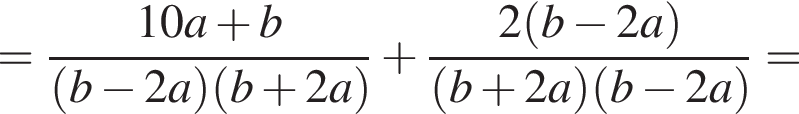
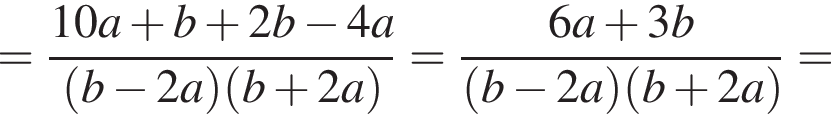
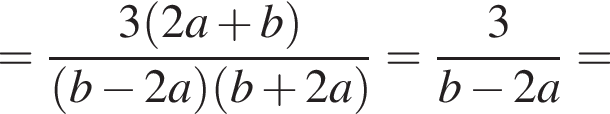
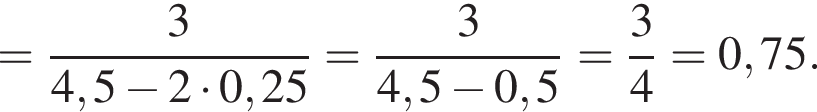
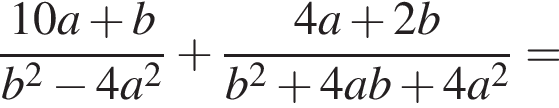
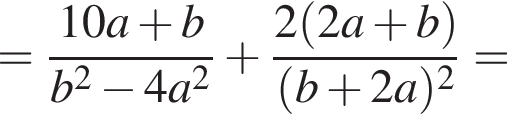
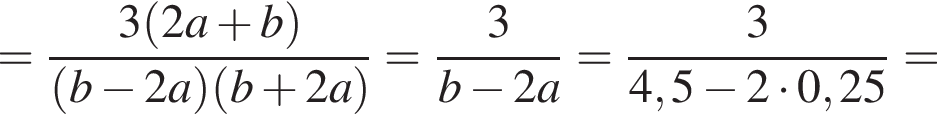
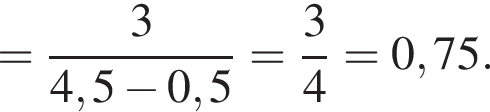
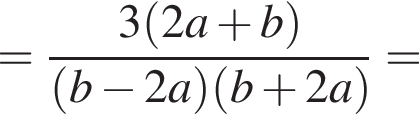
 тогда
тогда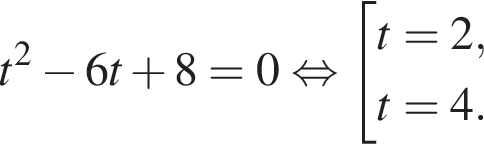
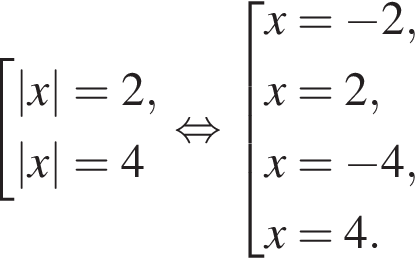
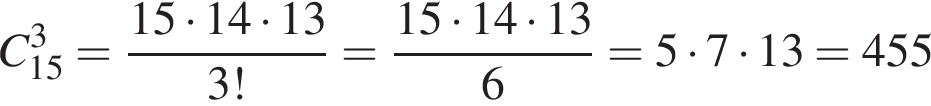
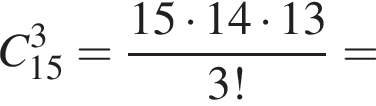
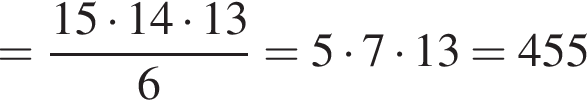
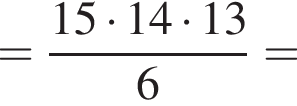
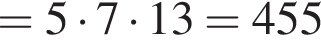
 вариантов.
вариантов.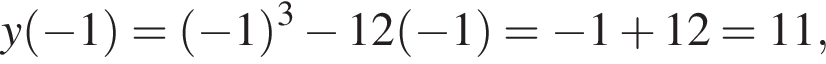
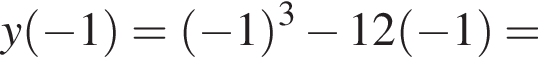
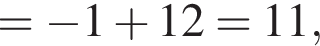
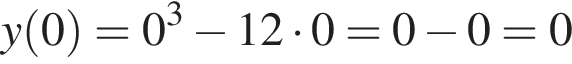
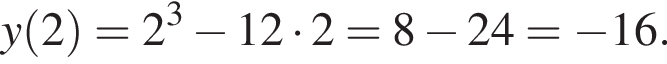
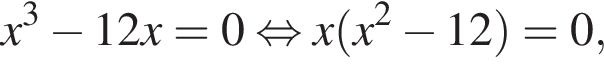 откуда
откуда 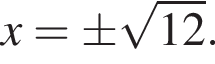 Возьмем производную:
Возьмем производную: 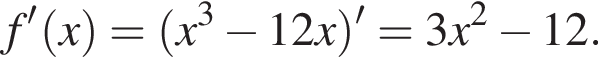 Решая уравнение
Решая уравнение 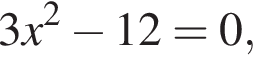 получим
получим 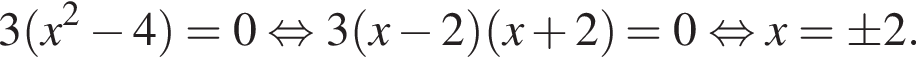
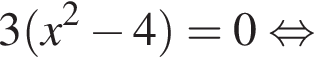
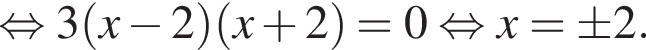
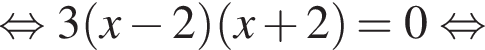

 и при
и при  (функция убывает). При
(функция убывает). При 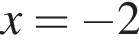 у функции максимум,
у функции максимум, 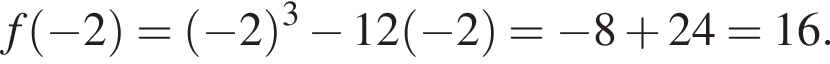
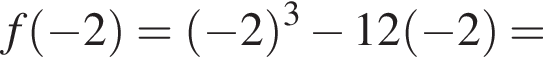
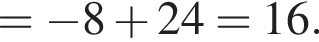
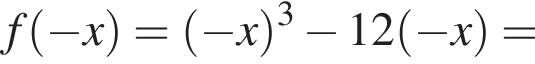
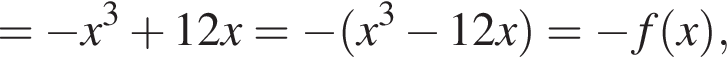
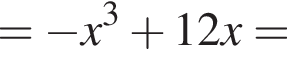
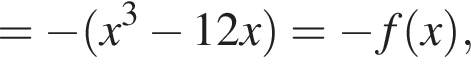

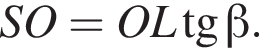
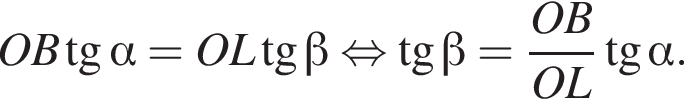
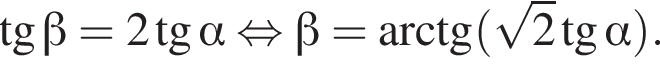
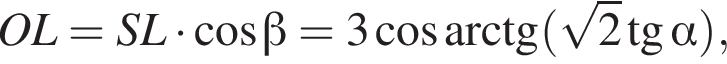
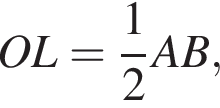 откуда
откуда 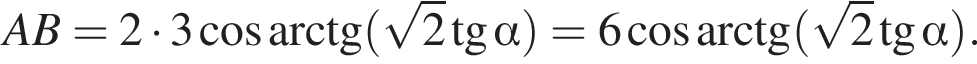
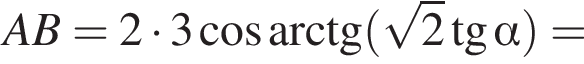

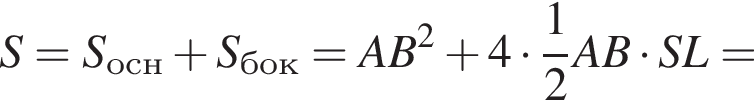
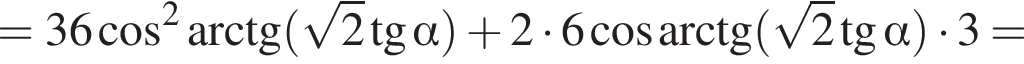
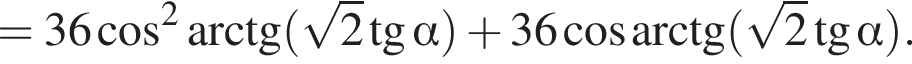
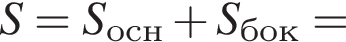
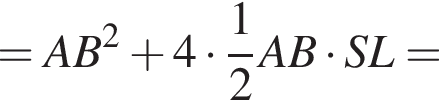
 3)
3) 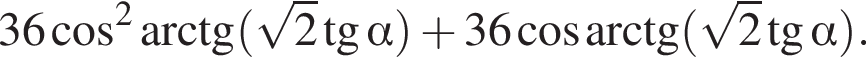
 то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
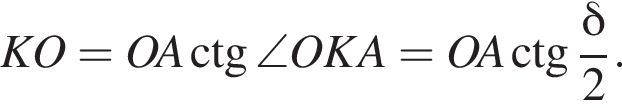
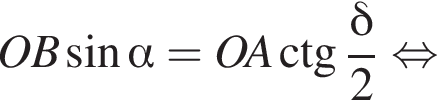
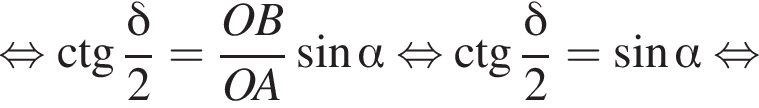
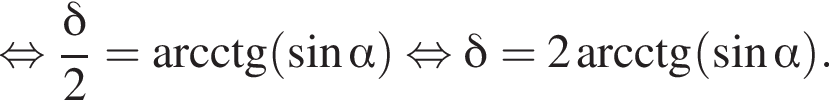
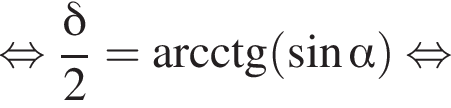

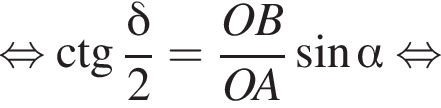
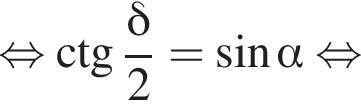
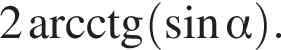

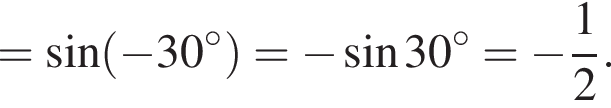
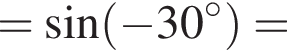
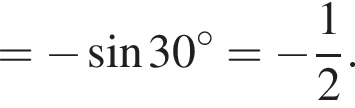
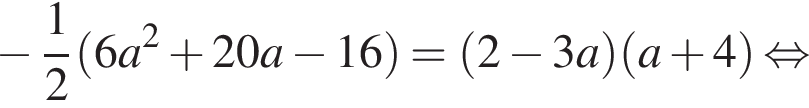

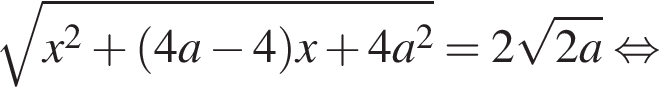
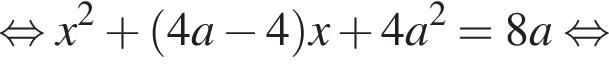
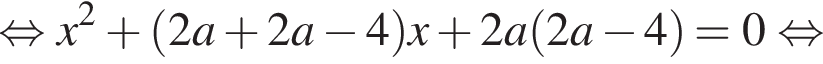
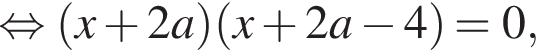
 или
или 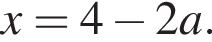 Ясно что эти корни всегда различны. Теперь найдем корни знаменателя:
Ясно что эти корни всегда различны. Теперь найдем корни знаменателя: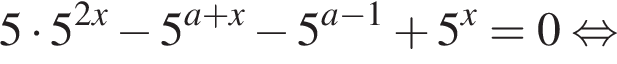
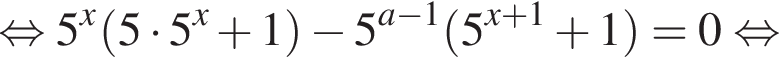
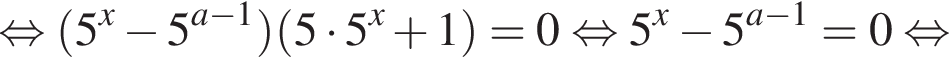
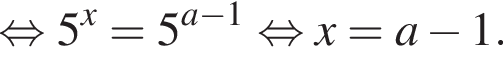
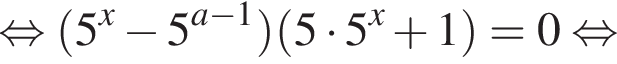
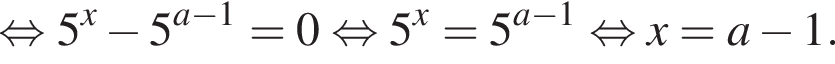
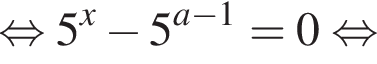
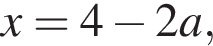 если они не совпадут с
если они не совпадут с 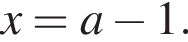 Когда это произойдет? Имеем:
Когда это произойдет? Имеем: 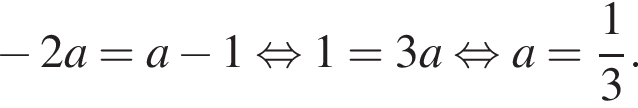
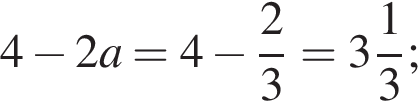
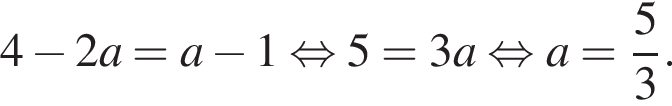
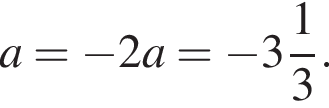

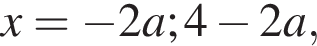 якщо
якщо 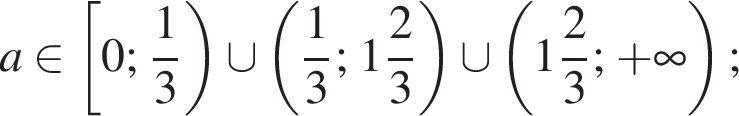
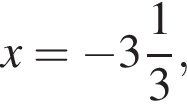 якщо
якщо 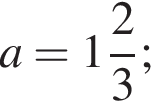
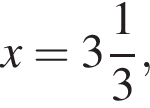 якщо
якщо