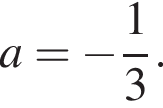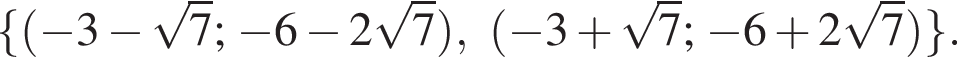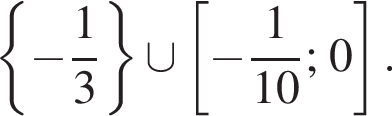На малюнку жирними точками показано добову кількість опадів, що випадали в Тернополі з 8 по 24 січня 2005 року. По горизонталі вказуються числа місяця, по вертикалі кількість опадів, що випали у відповідний день, в міліметрах. Для наочності жирні крапки малюнку з'єднані лінією. Визначте на малюнку, якого числа в Тернополі вперше випало рівно 1,5 міліметра опадів.
Копіювальна машина робить 3 копії за 4 секунди. Яку максимальну кількість копій можна одержати за 1 хвилину?
Площа повної поверхні циліндра дорівнює 92π, а площа його бічної поверхні — 56π. Визначте площу основи цього циліндра.
Обчисліть добуток коренів рівняння 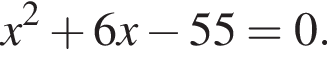
На малюнку зображено трикутник ABC, у якому ∠ ACB = 41°, ∠ AMN = 107°. Використовуючи дані малюнка, знайдіть градусну міру кута BAC.
На рисунку зображено графік функції
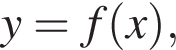 визначеної на проміжку [−4; 6]. Укажіть найбільше значення функції f на цьому проміжку.
визначеної на проміжку [−4; 6]. Укажіть найбільше значення функції f на цьому проміжку.
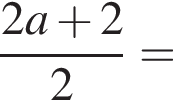
Довжину кола l можна обчислити за формулою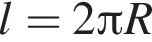 , де R - радіус кола (в метрах). Користуючись цією формулою, знайдіть радіус кола, якщо його довжина дорівнює 78 м. (Вважати
, де R - радіус кола (в метрах). Користуючись цією формулою, знайдіть радіус кола, якщо його довжина дорівнює 78 м. (Вважати![]() ).
).
Якому проміжку належить значення виразу 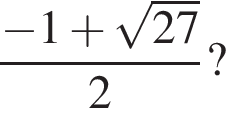
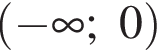

Які з наведених тверджень є правильними?
I. градусна міра розгорнутого кута дорівнює 180°.
II. У рівнобедреному трикутнику бісектриса, проведена до основи, є медіаною і висотою.
III. Площу рівностороннього трикутника можна знайти за формулою 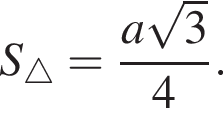
Розв’яжітьрівняння 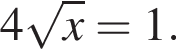
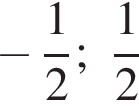
Знайдіть похідну функції 
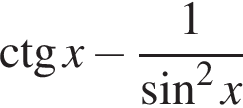
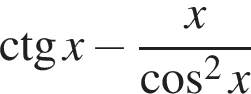
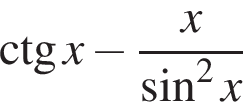
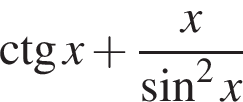
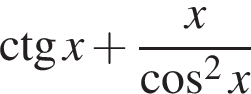
Розв’яжіть нерiвнiсть 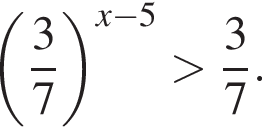
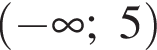
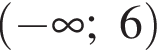


Знайдіть значення виразу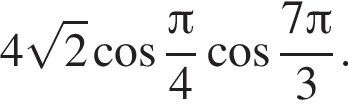
Основою прямої трикутної призми є прямокутний трикутник з катетами 9 і 40, бічне ребро призми дорівнює 50. Знайдіть площу бічної поверхні призми.
На відстані 60 м одна від одної ростуть дві сосни. Висота однієї 31 м, а іншої — 6 м. Знайдіть відстань (в метрах) між їх верхівками.
Установіть відповідність між функцією (1–3) та її властивістю (А–Д).
1. 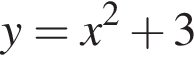
2. 
3. ![]()
A графік функції симетричний відносно осі у
Б графік функції розташований лише в першій координатній чверті
В функція набуває від’ємного значення в точці x = 2,4
Г графік функції проходить через початок координат
Д графік функції симетричний відносно початку координат
Установіть відповідність між виразом (1−3) і тотожно рівним йому виразом (А−Д), якщо a — довільне додатне число, a ≠ 1.
1. ![]()
2. ![]()
3. 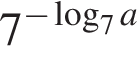
А ![]()
Б ![]()
В ![]()
Г a
Д −a
На рисунках (1−5) наведено інформацію про п’ять трикутників.
Установіть відповідність між запитанням (1−4) та правильною відповіддю на нього (А−Д).
1. На якому рисунку зображено трикутник, у якого центри вписаного й описаного кіл збігаються?
2. На якому рисунку зображено трикутник, один із внутрішніх кутів якого дорівнює 30°?
3. На якому рисунку зображено трикутник, площа якого дорівнює 10 см2?
4. На якому рисунку зображено трикутник, у якого діаметр описаного навколо нього кола дорівнює ![]() см?
см?
А Рис. 1
Б Рис. 2
В Рис. 3
Г Рис. 4
Д Рис. 5
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SO = 12, BD = 18. З єднайте початок речення (1–3) та його закінчення (А–Д) так, щоб утворилося правильне твердження.
1 Длина ребра SA
2 Площадь треугольника SOA
3 Косинус угла SAO
А 15
Б 54
В 26
Г 0,8
Д 0,6
ЗНО по физике сдавали 25 выпускников школы, что составляет треть от общего количества выпускников.
1. Сколько выпускников этой школы не сдавали экзамен по физике?
2. ЗНО по биологии сдавало 15 выпускников школы. На сколько процентов количество выпускников, сдавших физику, больше количества выпускников, сдавших биологию?
На рисунку зображено квадрат АВСD, сторона якого дорівнює 15. На сторонах АD і ВС квадрата вибрано точки К i М так, що АК = 4, МС = 3.
1. Визначте вiдстань мiж серединами вiдрiзкiв AB i KM.
2. Обчислiть довжину вiдрiзка KM.
У прямокутній системі координат у просторі початком вектора 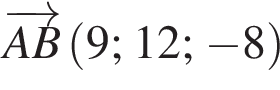 є точка
є точка 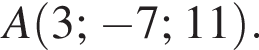
1. Визначте ординату точки В.
2. Обчисліть модуль вектора 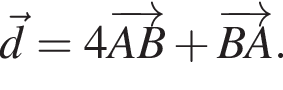
Добуток другого та четвертого членів геометричної прогресії дорівнює 36. Усі члени цієї прогресії є додатними.
1. Визначте третій член цієї прогресії.
Відповідь:
2. Визначте перший член цієї прогресії, якщо він удвічі більший за другий її член.
Відповідь:
На фабриці керамічного посуду 10% виготовлених тарілок мають дефект. Під час контролю якості продукції виявляється 80% дефектних тарілок. Інші тарілки надходять у продаж. Знайдіть ймовірність того, що випадково обрана при покупці тарілка не має дефектів. Результат округліть до сотих.
Перші 5 годин автомобіль їхав зі швидкістю 60 км/год, наступні 3 години зі швидкістю 100 км/год, а останні 4 години зі швидкістю 75 км/год. Знайдіть середню швидкість автомобіля протягом усього шляху.
Обчисліть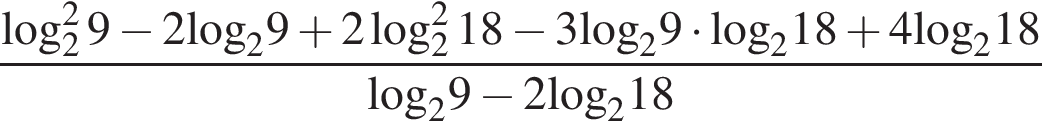 .
.
Розв'яжіть рівняння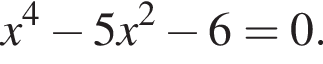 У відповідь запишіть добуток усіх його дійсних коренів.
У відповідь запишіть добуток усіх його дійсних коренів.
Музей має надати чотири картини відомого художника для виставки, присвяченої дню його народження. Одну картину вибирають з діючої експозиції музею, що містить 5 робіт цього художника, а трн інші — з архіву, у якому є 10 його картин. Скільки всього способів такого вибору?
| x | y |
|---|---|
| 0 | |
| 0 | |
| 9 |
Задано функцію 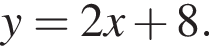
1. Для наведених у таблиці значень аргументу x і значень функції y визначте відповідні їм значення y та x (див. таблицу).
2. Запишіть координати точки М перетину графіка заданої функції з віссю x.
3. Знайдіть загальний вигляд первісних функції 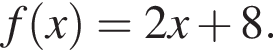
4. Знайдіть первісну F(x) функції f, графік якої проходить через точку M.
5. Побудуйте графік функції F.
6. Визначте область значень функції 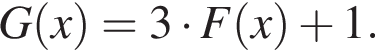
Висота правильної трикутної піраміди дорівнює 3. Бічні грані нахилені до основи під кутом β.
а) Зобразіть на малюнку цю піраміду та кут β.
б) Знайдіть площу повної поверхні піраміди.
в) Знайдіть об'єм піраміди.
Відповідно до умови завдання 31 (№ 3502) апофема правильної трикутної піраміди дорівнює 4. Бічні ребра нахилені до основи під кутом α.
а) Зобразіть на малюнку цю піраміду та вкажіть плоский кут при вершині.
б) Знайдіть цей кут.
Доведіть тотожність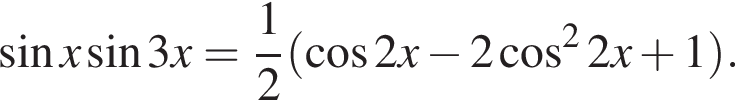
Задана система уравнений
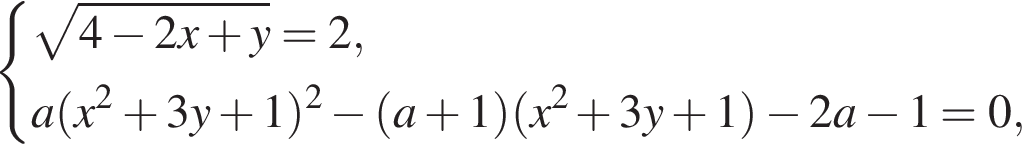
1. Решите систему уравнений при ![]()
2. Найдите все значения параметра a, при каждом из которых система уравнений имеет не более трех решений.

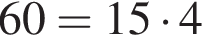 секунды можно сделать
секунды можно сделать 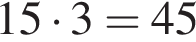 копий.
копий.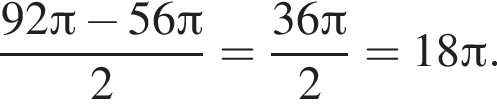
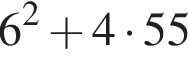 положителен. По теореме Виета их произведение равно его свободному члену, то есть −55.
положителен. По теореме Виета их произведение равно его свободному члену, то есть −55.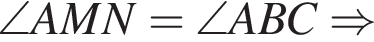
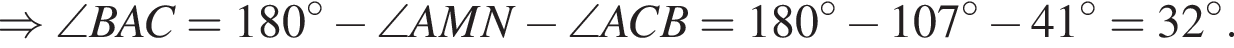
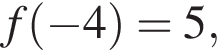 а все остальные точки графика находятся ниже этого уровня. Значит, ответ 5.
а все остальные точки графика находятся ниже этого уровня. Значит, ответ 5.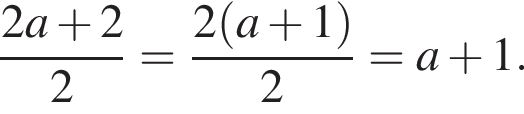
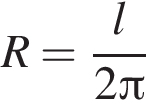
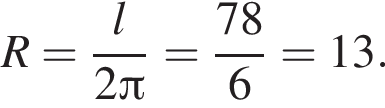
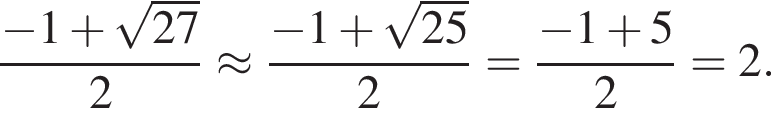
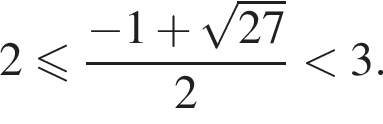 Заметим, что
Заметим, что  поэтому
поэтому 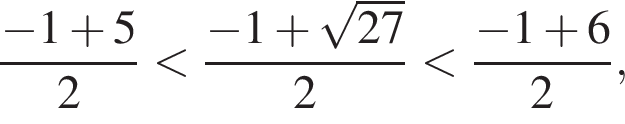
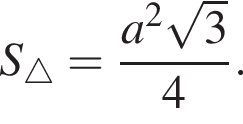
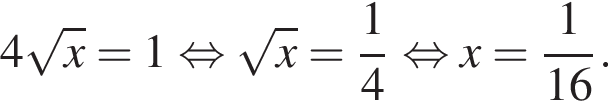
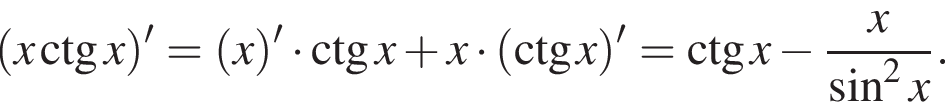

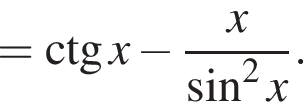


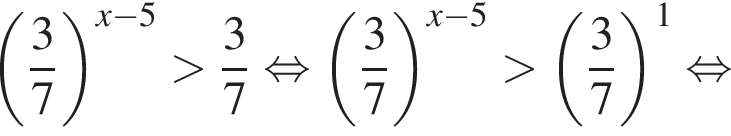
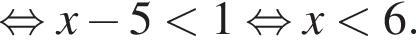
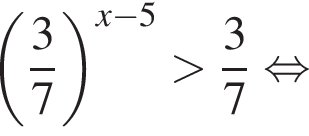
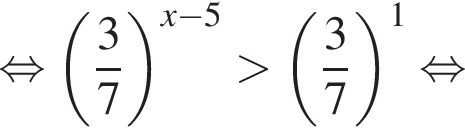
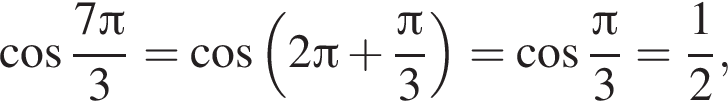
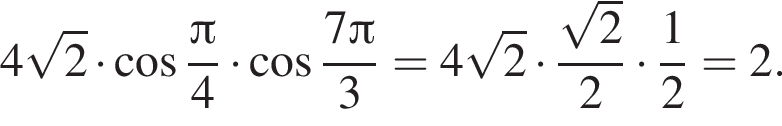
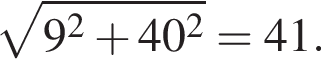
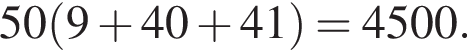
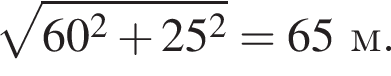
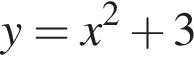 симметричен относительно оси Oy. Итак, 1 — А.
симметричен относительно оси Oy. Итак, 1 — А. приобретает отрицательное значение в точке с абсциссой, равной 2,4. Найдем это значение:
приобретает отрицательное значение в точке с абсциссой, равной 2,4. Найдем это значение: 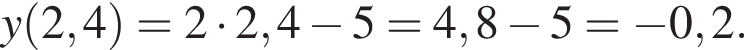
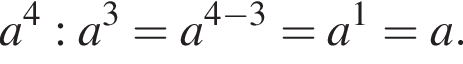
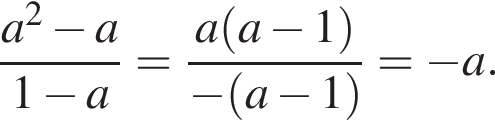
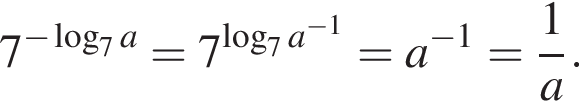
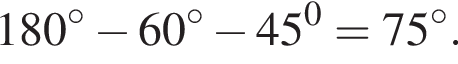 У пятого один угол тупой, а у двух других нетрудно найти тангенсы, они равны
У пятого один угол тупой, а у двух других нетрудно найти тангенсы, они равны 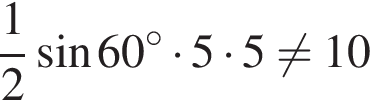 см2. Площадь второго
см2. Площадь второго 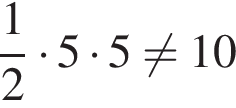 см2. У третьего второй катет больше 5, так как он лежит против большего угла, поэтому площадь его больше, чем
см2. У третьего второй катет больше 5, так как он лежит против большего угла, поэтому площадь его больше, чем 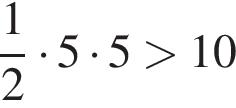 см2. У четвертого сторона напротив угла 60° больше, чем сторона напротив угла 45°, поэтому его площадь больше чем
см2. У четвертого сторона напротив угла 60° больше, чем сторона напротив угла 45°, поэтому его площадь больше чем 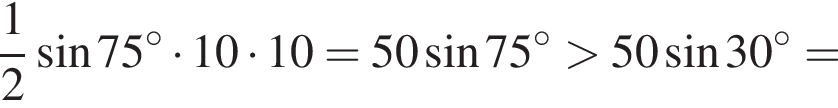
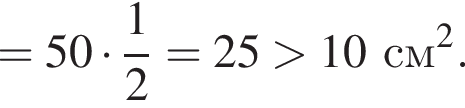
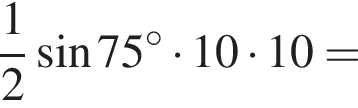
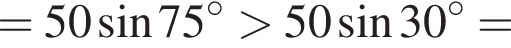
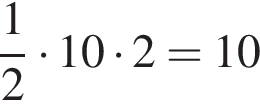 см2.
см2.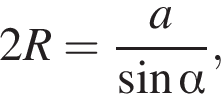 где α — угол напротив стороны длиной a в треугольнике. Тогда в первом треугольнике
где α — угол напротив стороны длиной a в треугольнике. Тогда в первом треугольнике 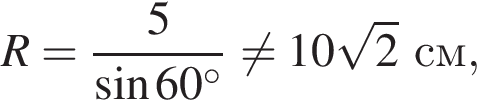
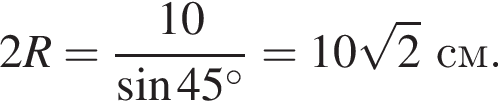
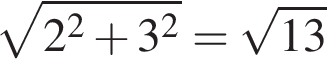 и
и 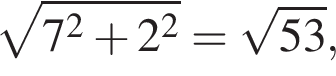 затем синус одного из углов
затем синус одного из углов 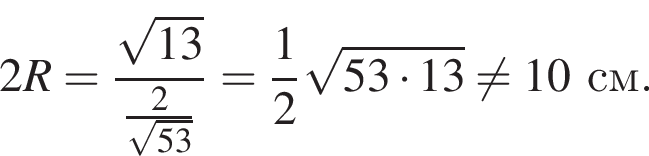

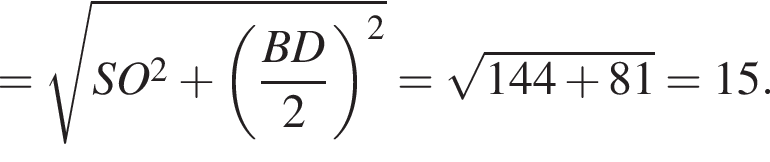
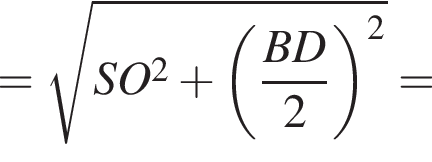
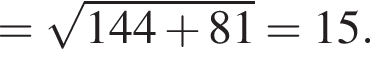
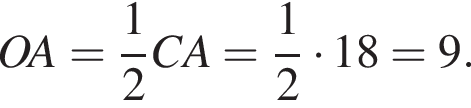
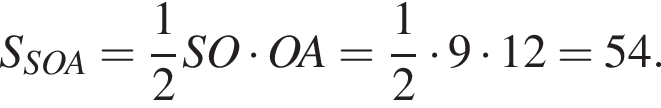
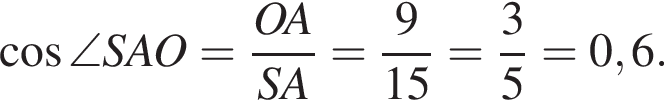
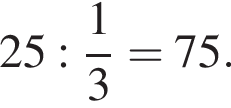 Следовательно,
Следовательно,  выпускников школы не сдавало экзамен по физике. Количество выпускников, сдавших физику, больше количества выпускников, сдавших биологию в
выпускников школы не сдавало экзамен по физике. Количество выпускников, сдавших физику, больше количества выпускников, сдавших биологию в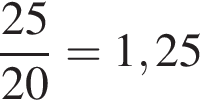
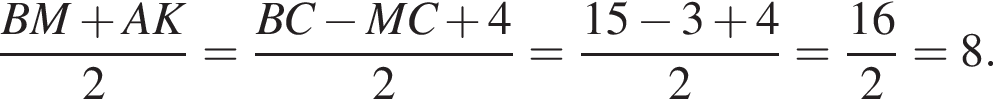
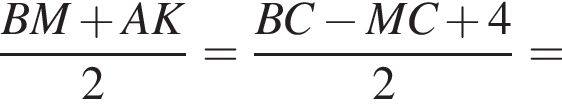
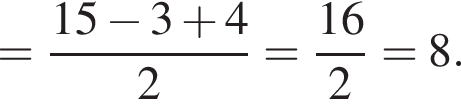

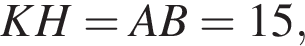
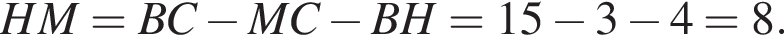

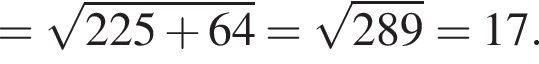

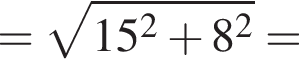
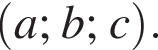 Тогда
Тогда 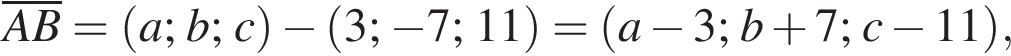


 и
и 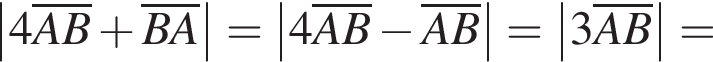
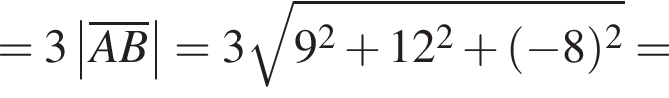
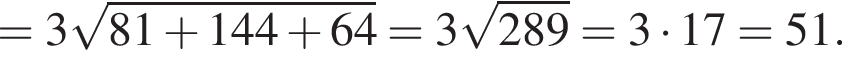
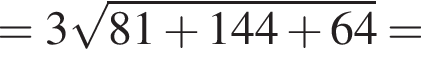
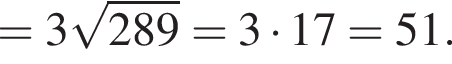
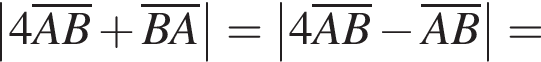

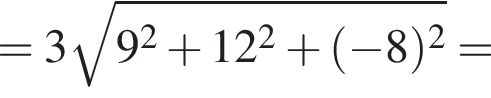
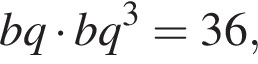 откуда
откуда 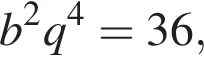
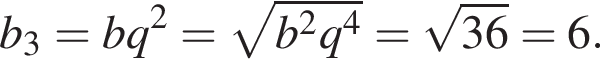
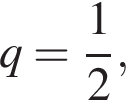 значит
значит 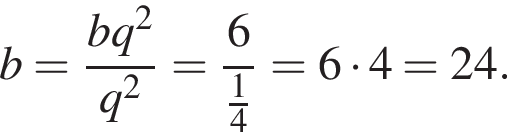
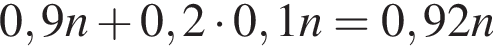 тарелок. Поскольку качественных из них
тарелок. Поскольку качественных из них 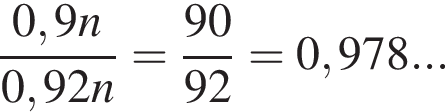
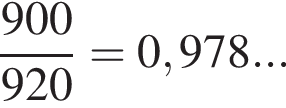
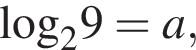 тогда
тогда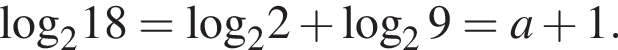
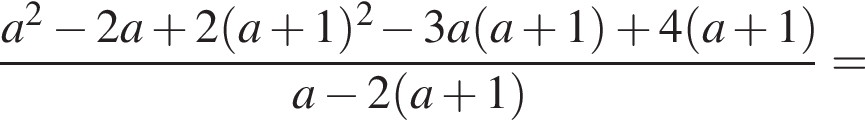
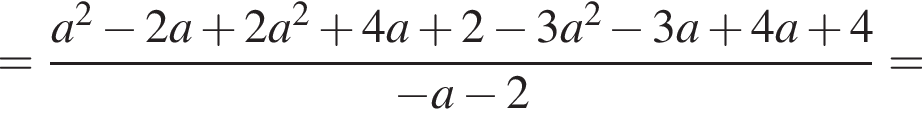
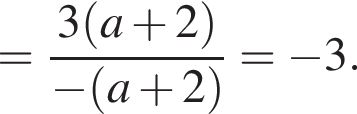
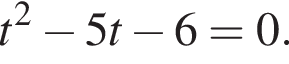
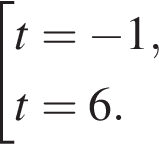
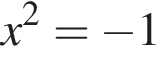 не имеет корней. Уравнение
не имеет корней. Уравнение 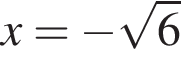 и
и 

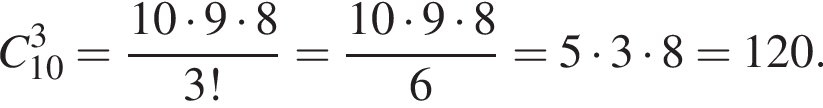
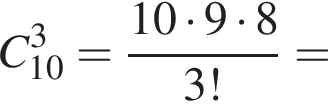
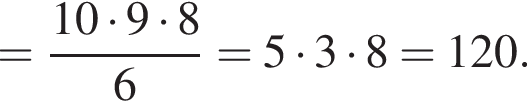
 способов.
способов. при
при  Если
Если 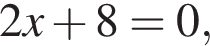 откуда
откуда 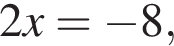
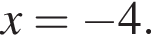 Отметим, что это и есть точка пересечения с горизонтальной осью, то есть
Отметим, что это и есть точка пересечения с горизонтальной осью, то есть 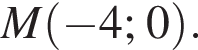
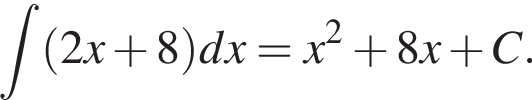
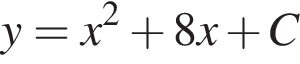 координаты точки M, находим
координаты точки M, находим 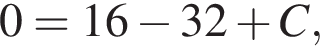 откуда
откуда  Итак,
Итак, 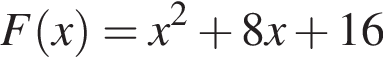 или
или 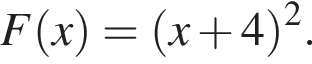
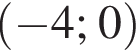
 принимает все значения из промежутка
принимает все значения из промежутка 

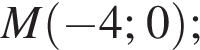
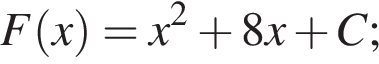
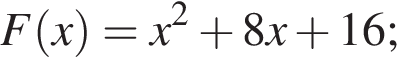
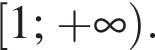
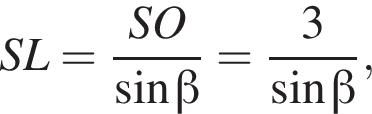

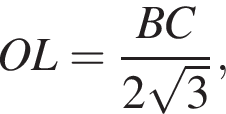 откуда
откуда 
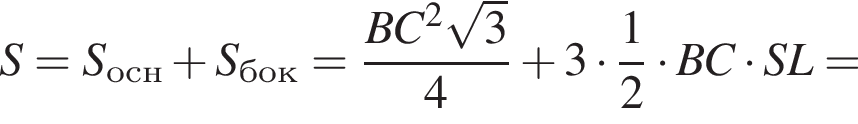
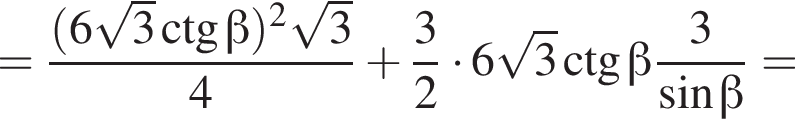

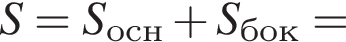
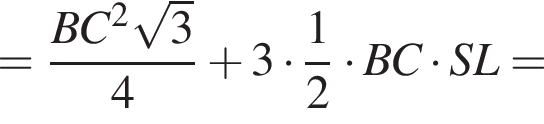
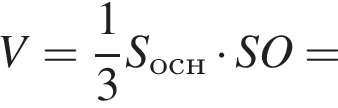
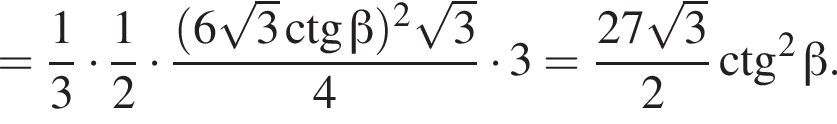
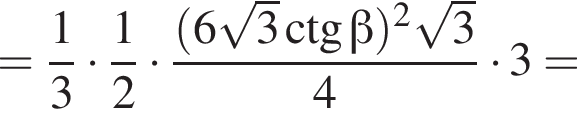
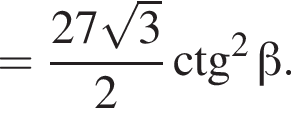
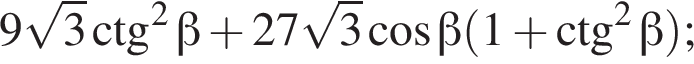 3)
3) 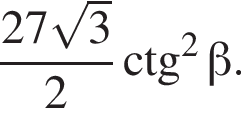
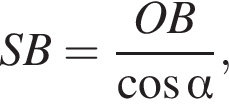
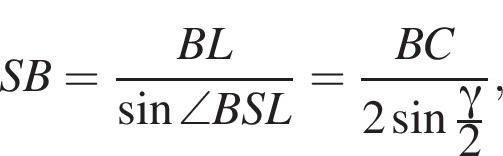
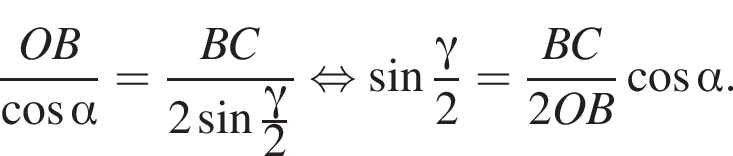
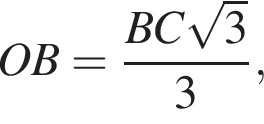 откуда:
откуда: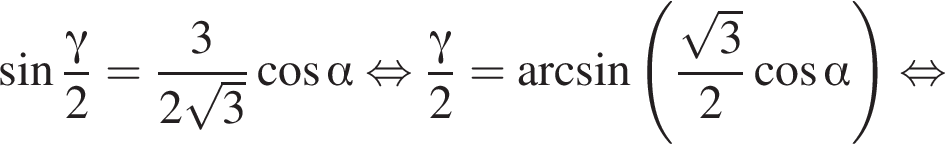
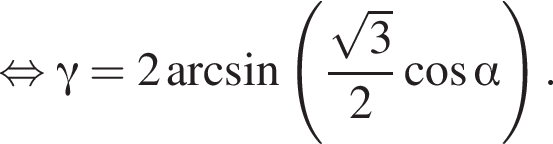
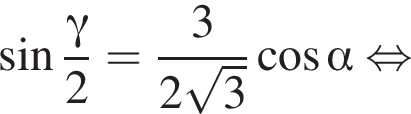
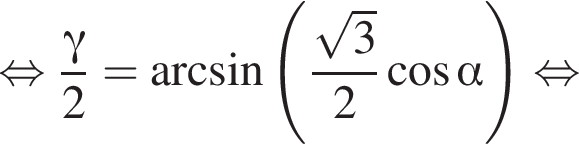
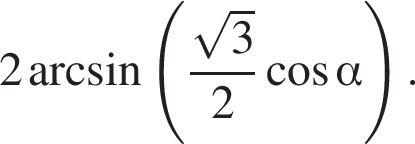
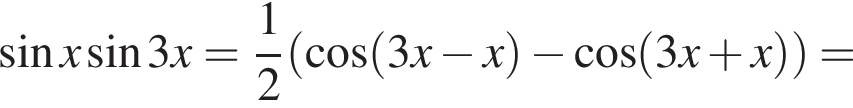
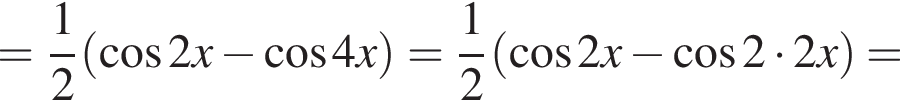
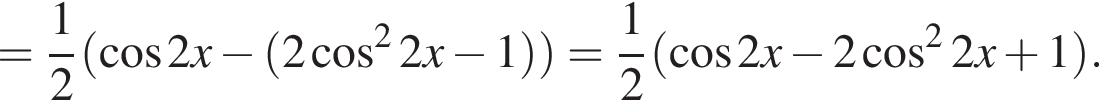
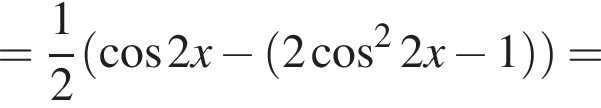
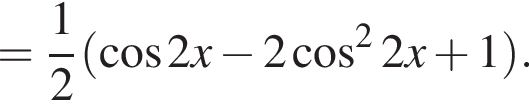
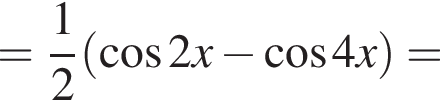


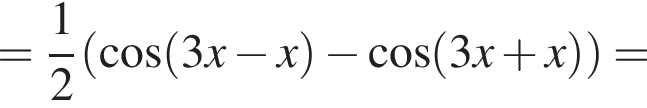
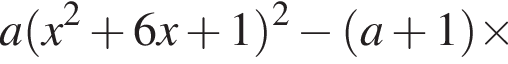
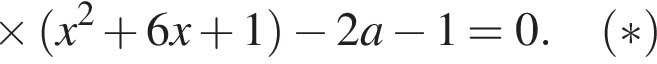
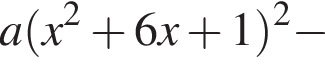
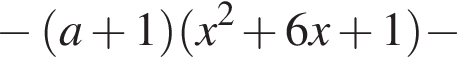
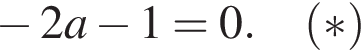

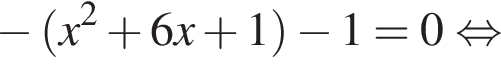
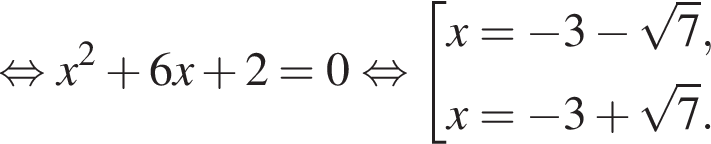
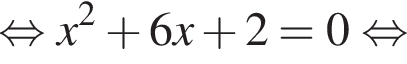
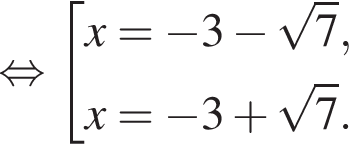
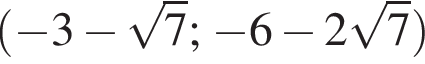 и
и 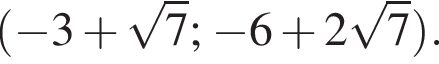
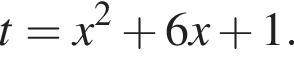 Заметим, что
Заметим, что 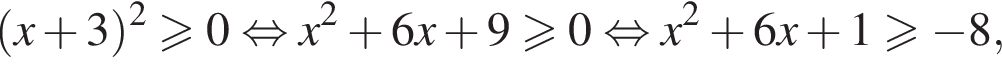
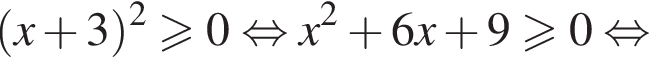
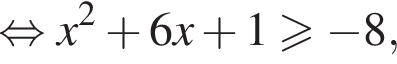
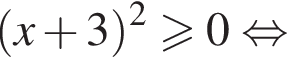
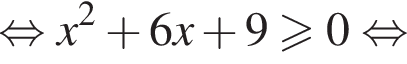
 Каждому значению
Каждому значению  соответствуют два значения переменной x, а значению
соответствуют два значения переменной x, а значению 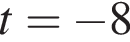 — одно значение переменной x. Тогда уравнение (⁎) записывается в виде
— одно значение переменной x. Тогда уравнение (⁎) записывается в виде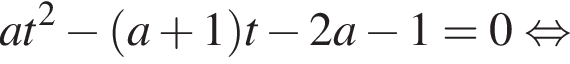
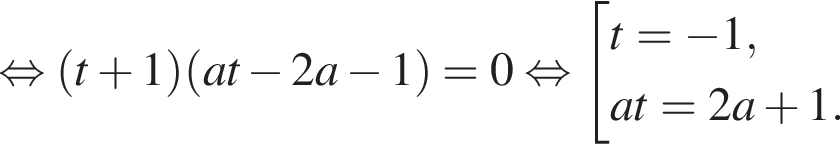
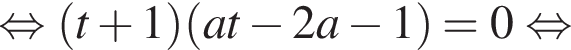
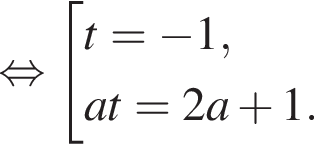
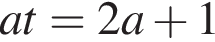 не имеет решений. Если
не имеет решений. Если 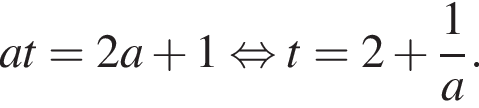
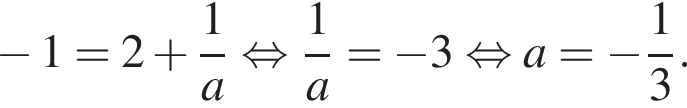
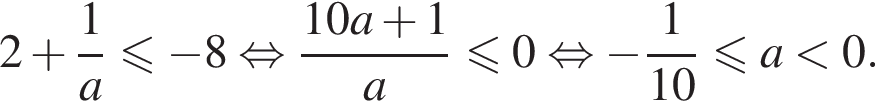
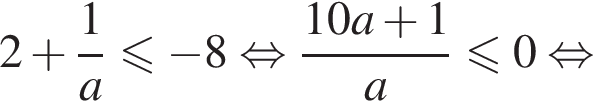
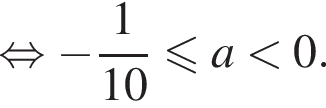
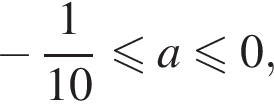 или при
или при