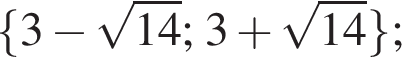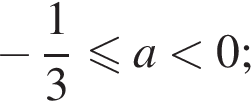На графіку відображено зміну робочої температури двигуна легкового автомобіля протягом 10 хвилин з моменту його запуску. Визначте за графіком кількість хвилин, протягом яких робоча температура двигуна була не більшою за 50 °С.
Равлик за день залазить на дерево на висоту 3 м, а за ніч спускається на 2 м. Висота дерева 10 м. За скільки днів равлик підніметься на вершину дерева?
Три ребра прямокутного паралелепіпеда, що виходять з однієї вершини, дорівнюють 4, 6, 9. Знайдіть ребро рівновеликого йому куба.
Яке з наведених чисел є коренем рівняння 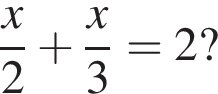
На рисунку зображено прямі m і n, що перетинаються. Визначте градусну міру кута γ, якщо

На рисунку зображено графік функції
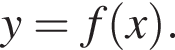 визначеної на проміжку [−3; 3]. Одна з наведених точок належить графіку функції
визначеної на проміжку [−3; 3]. Одна з наведених точок належить графіку функції  Укажіть цю точку.
Укажіть цю точку.
Спростіть вираз ![]()
Укажіть формулу для обчислення площі S бічної поверхні циліндра, довжина кола основи якого дорівнює l, а висота — h.
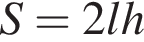
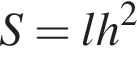
Результат спрощення виразу 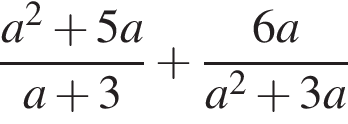 має вид:
має вид:
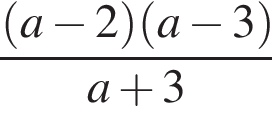
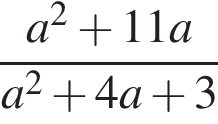
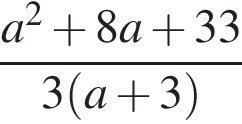
Які з наведених тверджень є правильними?
I. Якщо дуга кола становить 80°, то вписаний кут, що спирається на цю дугу, дорівнює 40°.
II. Якщо радіуси двох кіл дорівнює 5 і 7, а відстань між їх центрами дорівнює 3, то ці кола не мають спільних точок.
III. Якщо радіуси двох кіл дорівнюють 2 і 5, а відстань між їх центрами дорівнює 3, то ці кола торкаються.
Розв’яжіть систему рівнянь
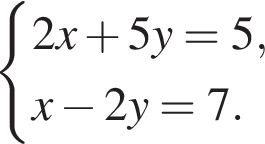
Використовуючи формулу Ньютона-Лейбніца, обчисліть 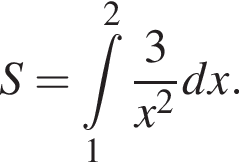
Розв’яжіть нерівність 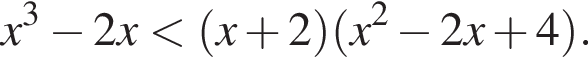
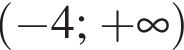
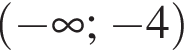
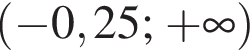


Обчислiть 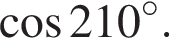
Правильна чотирикутна призма описана біля циліндра, радіус основи та висота якого дорівнюють 1. Знайдіть площу бічної поверхні призми.
На рисунку зображено ескіз емблеми. Емблема має форму кола радіуса 2 м, усередині якого розміщено 6 однакових півкіл. Один кінець кожного півкола збігається із центром кола, інший кінець лежить на колі. Для виготовлення емблеми (з усіма елементами включно) потрібен гнучкий матеріал вартістю 200 грн за 1 м довжини. Укажіть з-поміж наведених сум грошей найменшу, якої достатньо, шоб придбати цей матеріал для виготовлення емблеми. Уважайте, що на з'єднання елементів емблеми не потрібно додаткових витрат матеріалу.
Установіть відповідність між функцією (1−3) і властивістю (А−Д) її графіка
1. 
2. 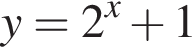
3. 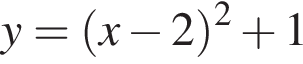
А возрастает на всей области определения
Б убывает на всей области определения
В нечетная
Г не определена в точке x = 0.
Д пересекает прямую 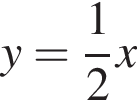 в одной точке.
в одной точке.
Установіть відповідність між числовим виразом (1—4) та його значенням (А—Д).
1. 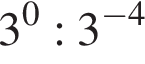
2. 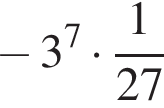
3. 
4. 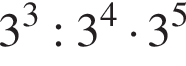
А 243
Б −81
В ![]()
Г ![]()
Д 81
На рисунку зображено квадрат ABCD і ромб CKMD, які лежать в одній площині. Периметр ромба дорівнює 48 см, а його гострий кут — 60°. До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
1. Довжина сторони квадрата ABCD дорівнює
2. Довжина більшої діагоналі ромба CKMD дорівнює
3. Відстань від точки М до сторони CD дорівнює
4. Відстань від точки К до прямої AD дорівнює
А 6 см
Б 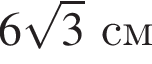
В 12 см
Г 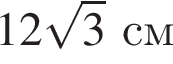
Д 18 см
На рисунку зображено куб АВСDА1B1C1D1. Установіть відповідність між парою прямих (1−4) та їх взаємним розташуванням (А−Д).
1 AC й CC1
2 AB1 i CD1
3 AC й CD1
4 AB1 i C1D
А прямі паралельні
Б прямі мимобіжні
В прямі перетинаються й утворюють прямий кут
Г прямі перетинаються й утворюють кут 45°
Д прямі перетинаються й утворюють кут 60°
На клумбі висадили рядами 125 кущів троянд з однаковою кількістю кущів у кожному ряду. Виявилось, що кількість рядів на 20 менша за кількість кущів у кожному ряду.
1. Скільки висадили кущів троянд у кожному ряду?
2. Узимку в першому ряду зазнали ушкоджень 16% кущів троянд. Скільки кущів троянд у першому ряду перезимували неушкодженими?
У прямокутному трикутнику ABC
 відстані від середини медіани BM до катетів АС і BC дорівнюють 5 см і 6 см відповідно.
відстані від середини медіани BM до катетів АС і BC дорівнюють 5 см і 6 см відповідно.
1. Визначте довжину катета AC (у см).
2. Визначтеї радіус (у см) кола, описаного навколо трикутника ABC.
В прямоугольной системе координат в прострастве задан вектор 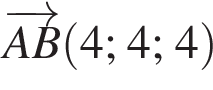 с началом в точке A(−1; 2; 1).
с началом в точке A(−1; 2; 1).
1. Найдите ординату точки B.
2. Точка C имеет координаты (3; −2; 2). Найти скалярное произведение 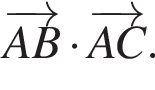
У геометричній прогресії сума першого та другого членів дорівнює 75, а сума другого та третього членів дорівнює 150.
1. Найдите первый член этой прогрессии.
2. Найдите третий член этой прогрессии.
У магазині три продавці. Кожен із них зайнятий з клієнтом із ймовірністю 0,3. Знайдіть ймовірність того, що у випадковий момент часу всі три продавці зайняті одночасно (вважайте, що клієнти заходять незалежно один від одного).
У таблиці відображено інформацію про ціну та кількість зошитів, придбаних за цією ціною Олексієм. За даними таблиці визначте середню ціну (у грн) одного зошита з придбаних Олексієм.
| Ціна одного зошита, грн | 8 | 10 | 12 |
|---|---|---|---|
| Кількість зошитів | 9 | 4 | 7 |
Обчисліть значення виразу
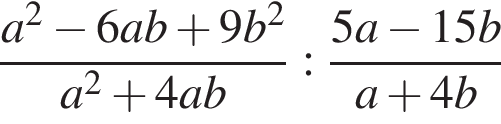
при  i
i 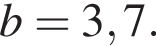
Розв’яжіть рівняння 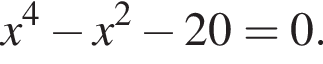 У відповіді запишіть добуток усіх його дійсних коренів.
У відповіді запишіть добуток усіх його дійсних коренів.
Довідкову інформацію промовляють почергово по одному разу п’ятьма мовами: українською, англійською, німецькою, російською та польською. Скільки всього є варіантів послідовностей озвучування цієї інформації цими п’ятьма мовами, якщо спочатку її промовляють українською?
| x | y |
|---|---|
| −2 | |
| 1 | |
| 2 |
Задано функцію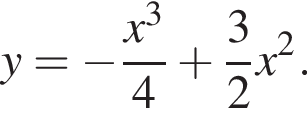
1. Для наведених у таблиці значень аргументів х визначте відповідні їм значення у (див. таблицю).
2. Визначте та запишіть координати точок перетину графіка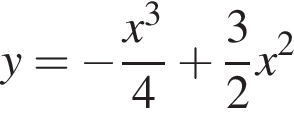 з віссю x .
з віссю x .
3. Знайдіть похідну f' функції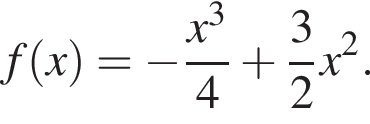
4. Визначте нулі функції f' .
5. Визначте проміжки зростання та спадання, точки екстремуму функції f .
6. Побудуйте ескіз графіка функції f .
Сторона основи правильної трикутної піраміди дорівнює 4. Бічні ребра нахилені до основи під кутом α.
1. Зобразіть на малюнку цю піраміду та кут α.
2. Знайдіть бічне ребро піраміди.
3. Знайдіть площу повної поверхні піраміди.
Відповідно до умови завдання 31 (№ 3518) сторона основи правильної чотирикутної піраміди дорівнює 4. Бічні грані нахилені до основи під кутом β.
а) Зобразіть на малюнку цю піраміду та побудуйте лінійний кут двогранного кута при бічному ребрі.
б) Знайдіть цей кут.
Доведіть тотожність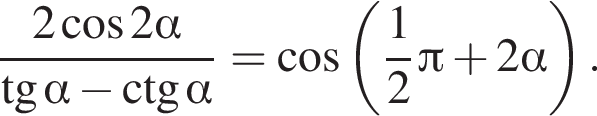
Задано рівняння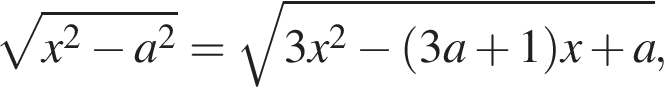 де x – змінна, a – параметр.
де x – змінна, a – параметр.
1. Розв'яжіть рівняння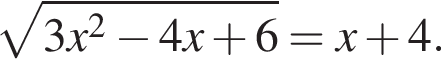
2. Знайдіть усі значення a , при кожному з яких рівняння має рівно один корінь на відрізку [0; 1].

 Из графика видно, что по прошествии трех минут температура составила 50 градусов и ниже уже не опускалась, поэтому ответ 3 минуты.
Из графика видно, что по прошествии трех минут температура составила 50 градусов и ниже уже не опускалась, поэтому ответ 3 минуты.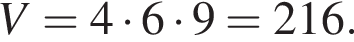

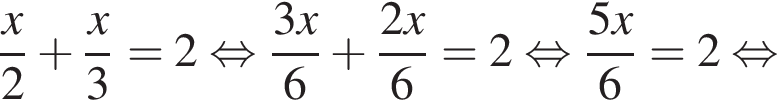
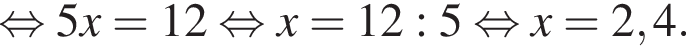
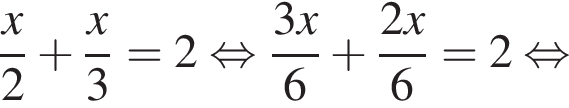
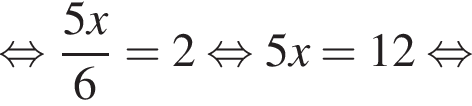
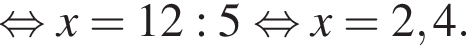
 откуда
откуда  Тогда
Тогда 
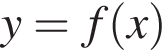 и
и  симметричны относительно оси Ox.
симметричны относительно оси Ox.
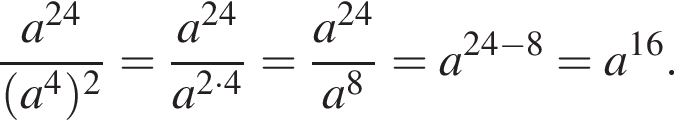
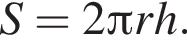 При этом
При этом 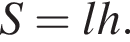
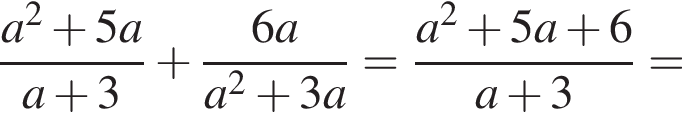
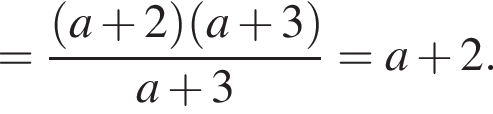
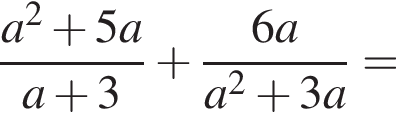
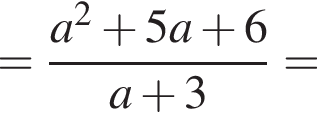
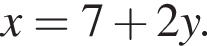 Подставляя в первое, находим
Подставляя в первое, находим 
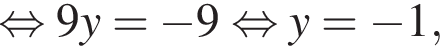


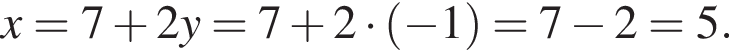

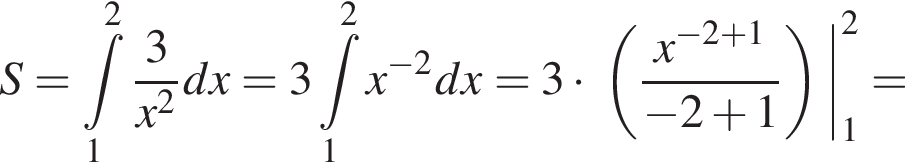
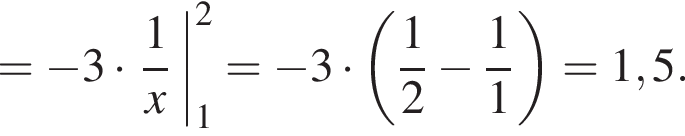
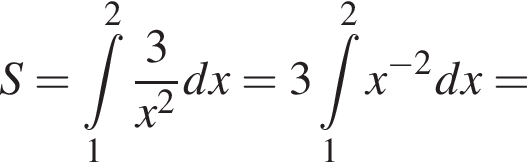

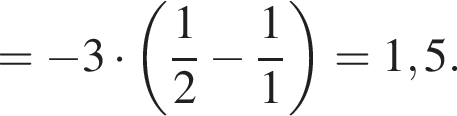
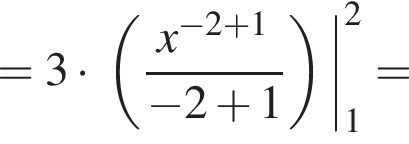
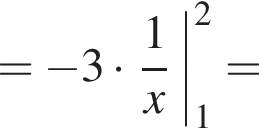
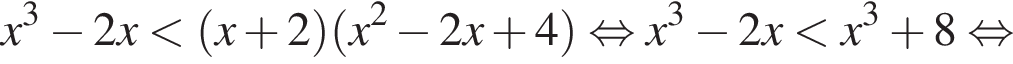
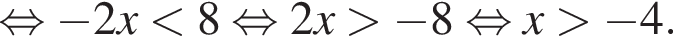
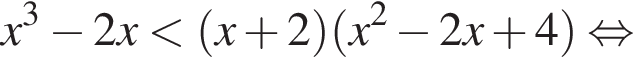
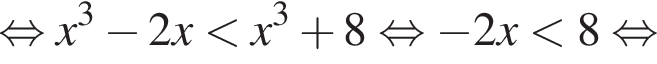
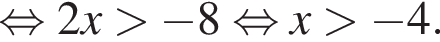
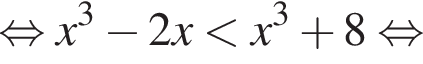
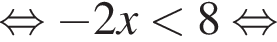
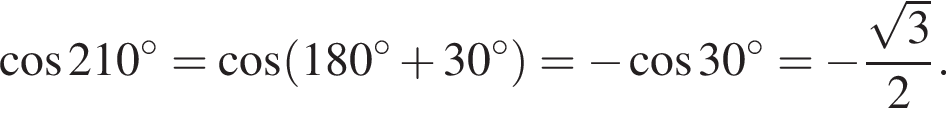

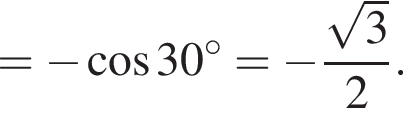
 метров, а длина полукругов — дополнительно
метров, а длина полукругов — дополнительно 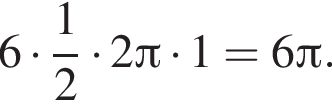 Итого требуется
Итого требуется  метров материала, который будет стоить
метров материала, который будет стоить 
 Следовательно, 1 — В.
Следовательно, 1 — В.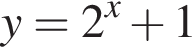 возрастает на всей области определения. Таким образом, 2 — А.
возрастает на всей области определения. Таким образом, 2 — А.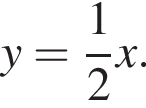 Таким образом, 3 — Д.
Таким образом, 3 — Д.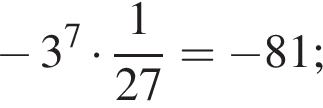
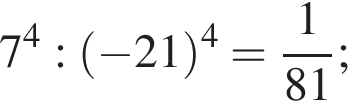
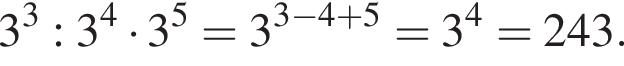
 тогда
тогда 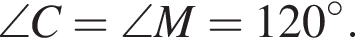 Большей диагональю ромба является KD. Применим теорему косинусов в треугольнике CKD:
Большей диагональю ромба является KD. Применим теорему косинусов в треугольнике CKD: 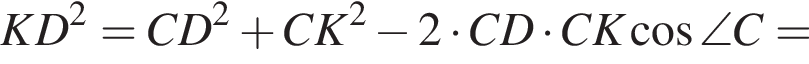
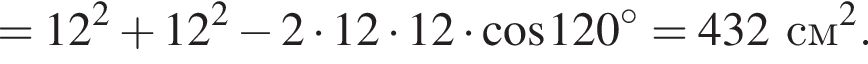
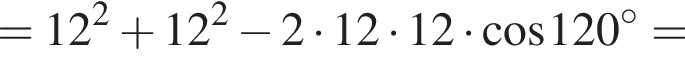
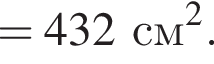
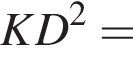
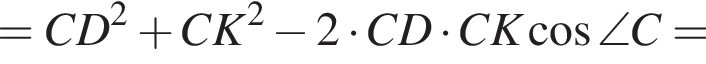
 Итак, 2 — Г.
Итак, 2 — Г.  Имеем:
Имеем:
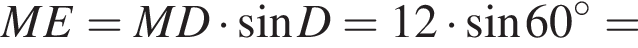
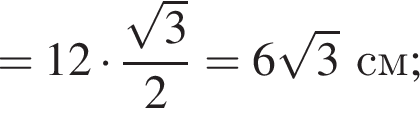
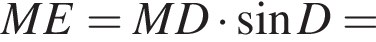

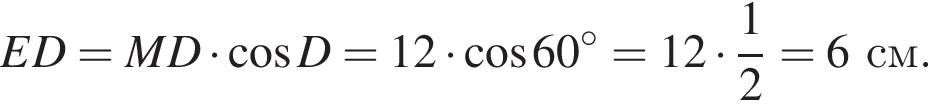
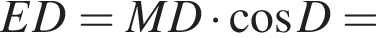
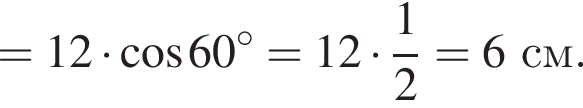

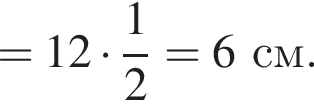

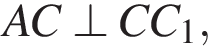 потому что
потому что 
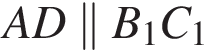 как ребра параллелепипеда и
как ребра параллелепипеда и  Значит, AB1C1D — параллелограмм, поэтому
Значит, AB1C1D — параллелограмм, поэтому 
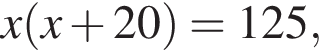 откуда
откуда 
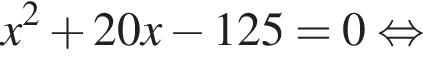
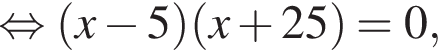
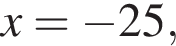 что невозможно. Значит в каждом ряду по
что невозможно. Значит в каждом ряду по 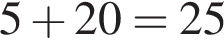 кустов. Из 25 кустов в первом ряду получили повреждения
кустов. Из 25 кустов в первом ряду получили повреждения 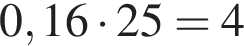 куста, а остальные
куста, а остальные 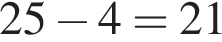 куст перезимовали без повреждений.
куст перезимовали без повреждений. м
м см
см см.
см.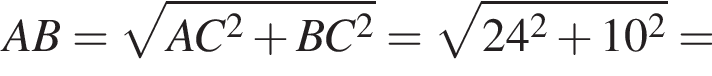

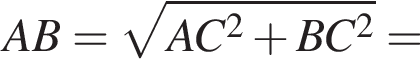
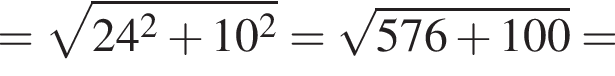
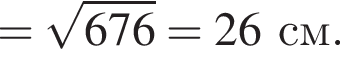
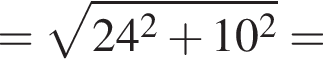
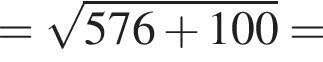
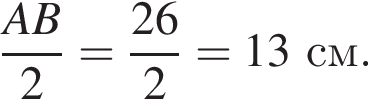
 Тогда
Тогда 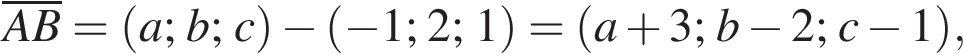
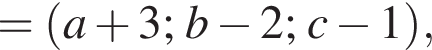
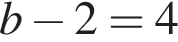 и
и 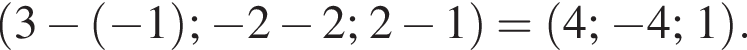
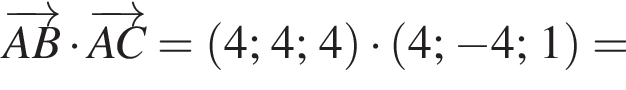
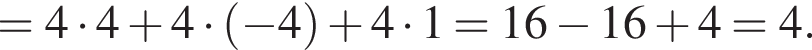

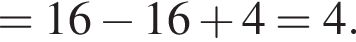
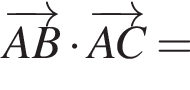
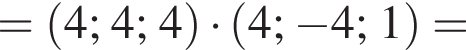
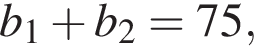
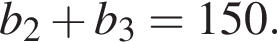 Запишем эти равенства в виде системы уравнений на первый член и знаменатель прогрессии и решим эту систему:
Запишем эти равенства в виде системы уравнений на первый член и знаменатель прогрессии и решим эту систему: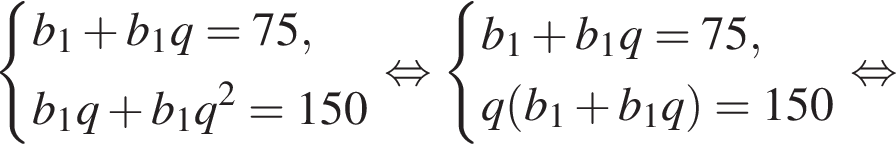
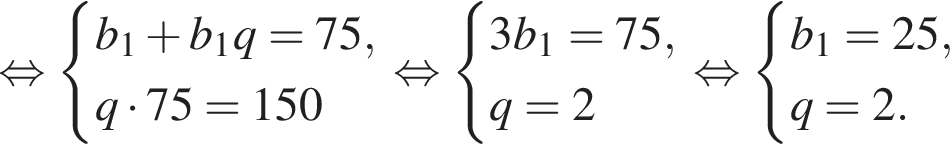
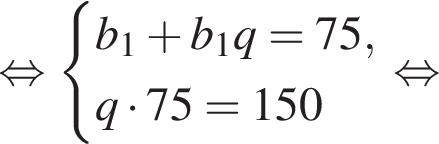
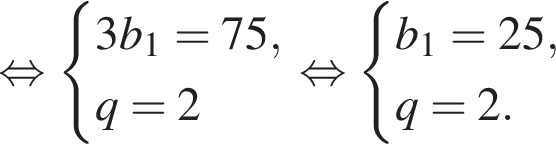
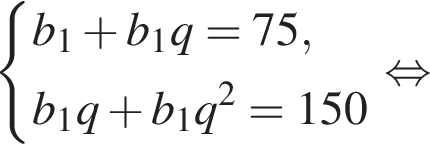
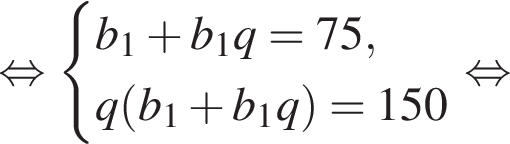
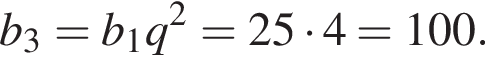

 тетрадей Алексей заплатил
тетрадей Алексей заплатил 
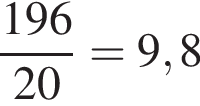 гривны.
гривны.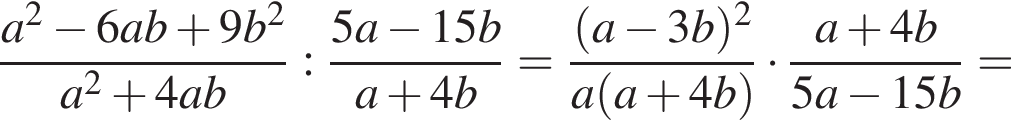
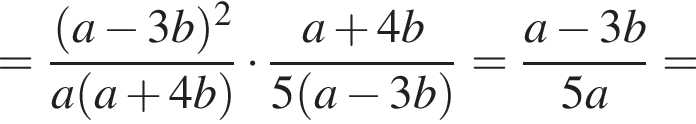
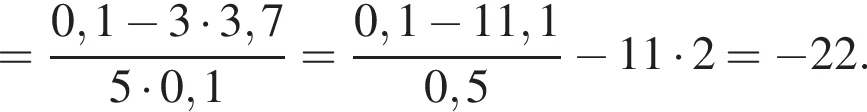
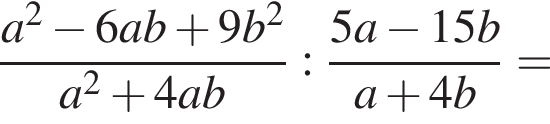
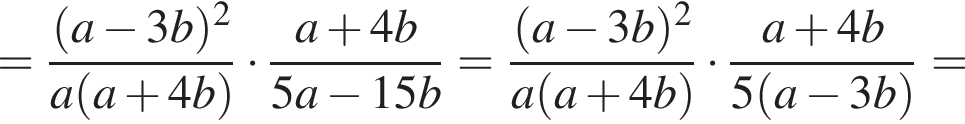
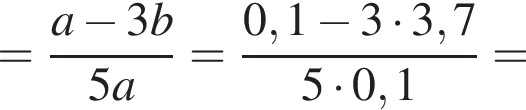
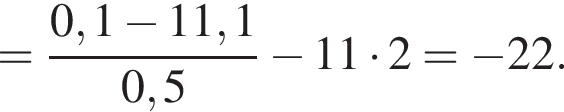
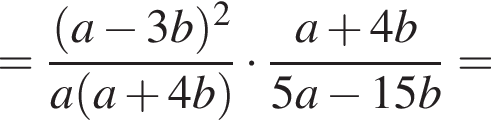
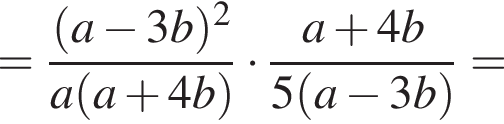
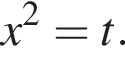 Уравнение примет вид
Уравнение примет вид 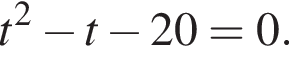 Решая его, получим
Решая его, получим  Уравнение
Уравнение 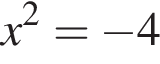 корней не имеет. Произведение корней таким образом равно
корней не имеет. Произведение корней таким образом равно 
 способами.
способами.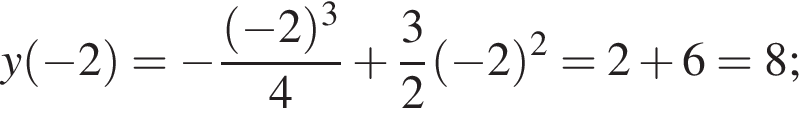
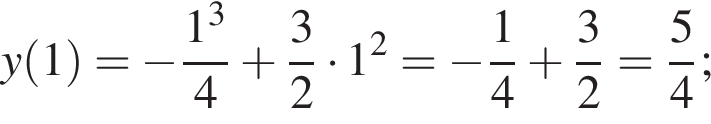
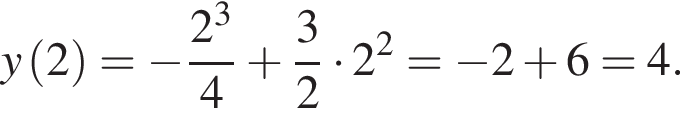
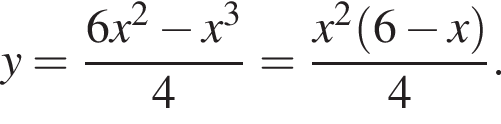
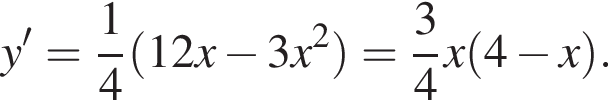
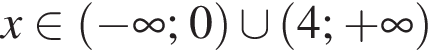 и
и  Поэтому функция убывает на промежутках
Поэтому функция убывает на промежутках 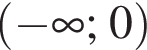 и
и  возрастает на промежутке
возрастает на промежутке  и
и 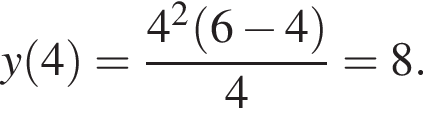 График представлен на рисунке.
График представлен на рисунке.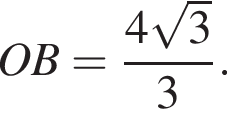 Выразим боковое ребро SB пирамиды из прямоугольного треугольника SOB, получим:
Выразим боковое ребро SB пирамиды из прямоугольного треугольника SOB, получим: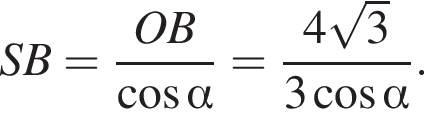
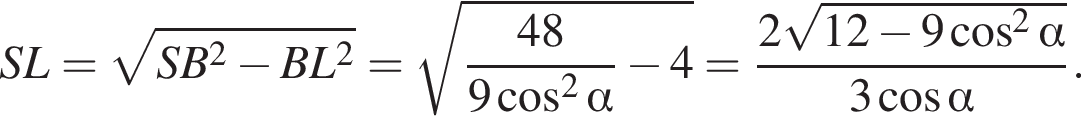
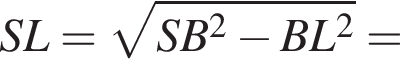
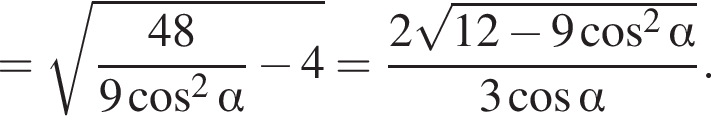
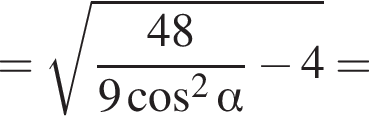
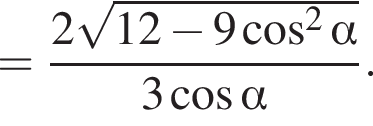
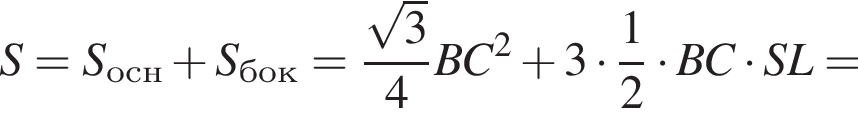
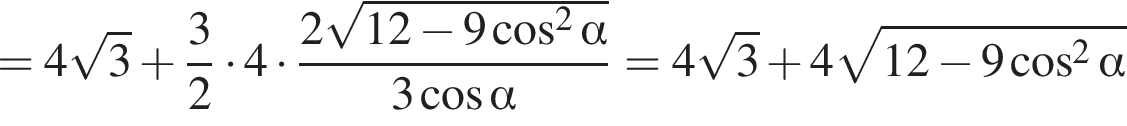
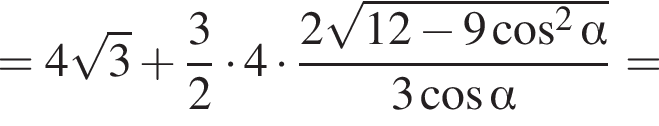
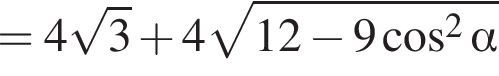
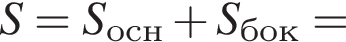
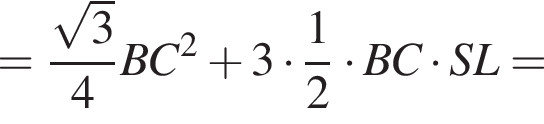
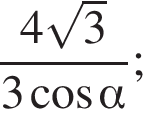 3)
3) 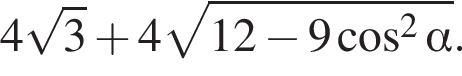
 то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.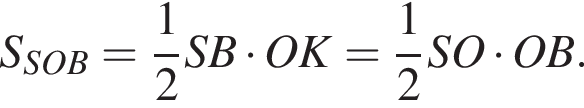
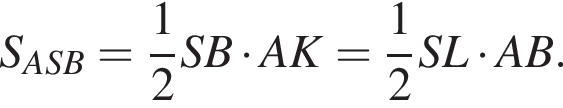
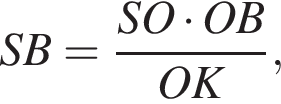
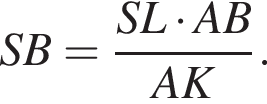
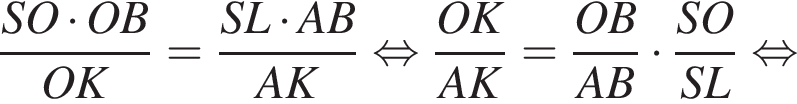

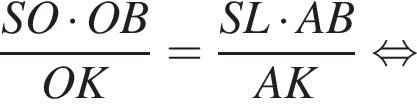
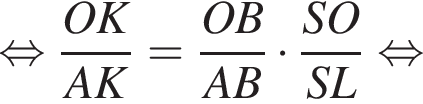
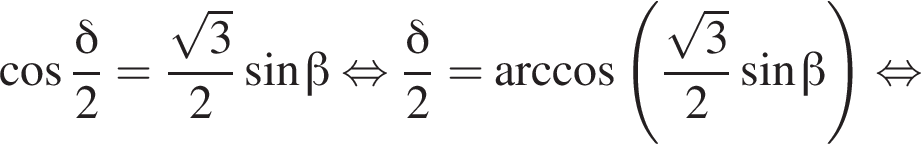
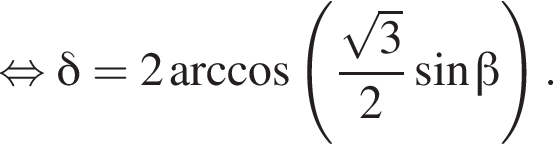
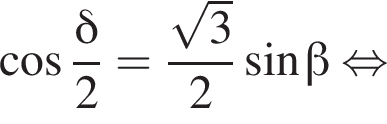
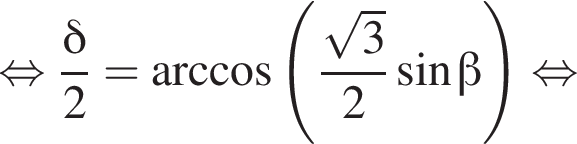
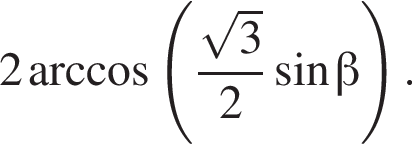

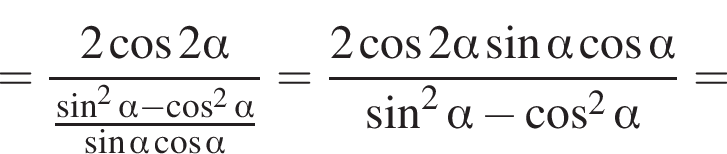
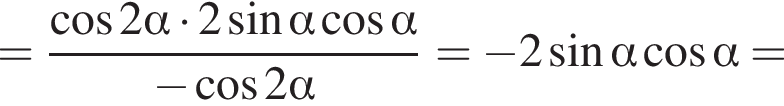
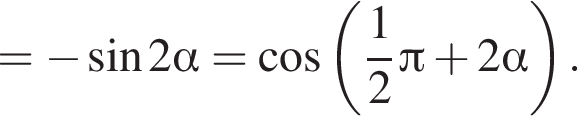
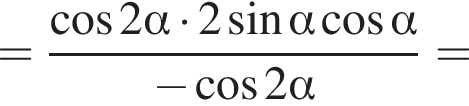
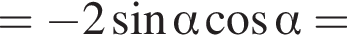
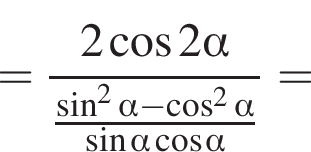
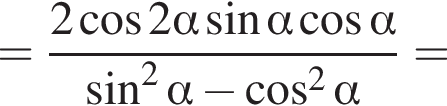

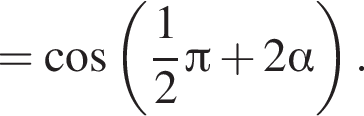
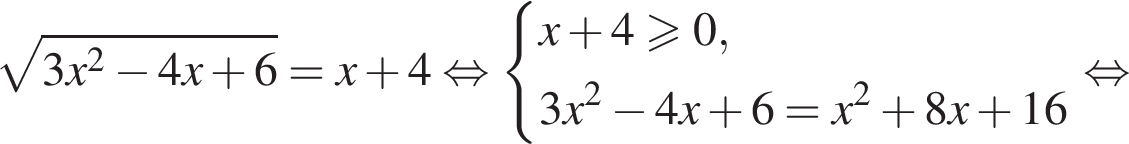
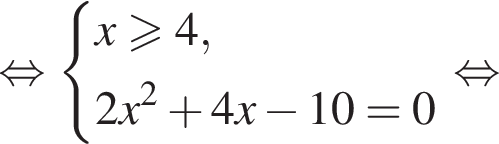
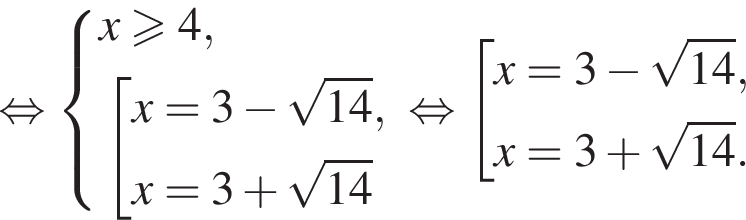
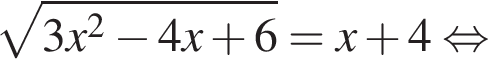
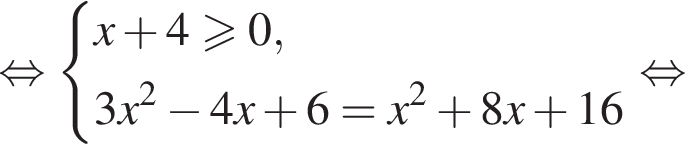
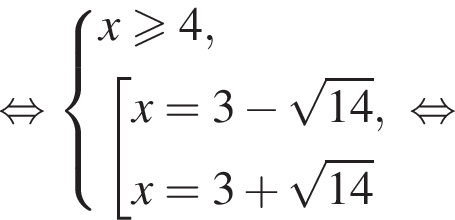
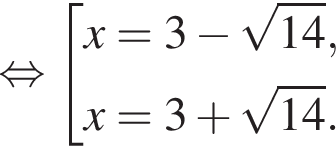

 Получаем
Получаем 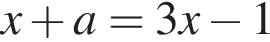 при условии
при условии  Получаем
Получаем 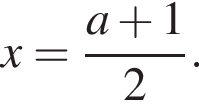 Условие принимает вид:
Условие принимает вид: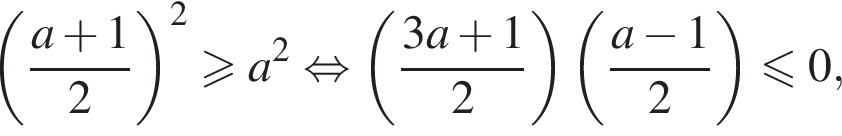
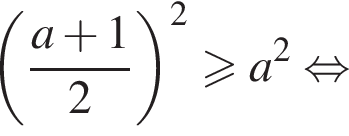
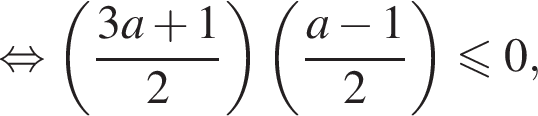
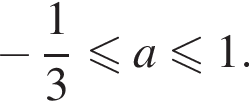 То есть в этом случае
То есть в этом случае 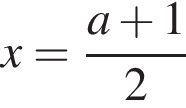 при
при 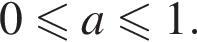
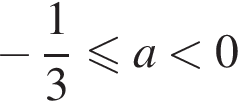 и
и