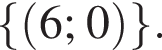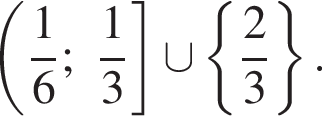На малюнку показано зміну біржової вартості акцій целюлозно-паперового заводу у першій половині квітня. 2 квітня бізнесмен придбав 250 акцій цього заводу по 290 грн за штуку. 6 квітня він продав 150 акцій по 260 грн за штуку, а акції, що залишилися, продав 11 квітня по 200 грн за штуку. Скільки гривень втратив бізнесмен унаслідок цих операцій?
Один кілограм яблук коштує на базарі від 9 грн до 12 грн, а один кілограм груш — від 19 грн до 25 грн. Оксана заплатила за куплені на базарі 2 кг яблук та 3 кг груш m гривень. Укажіть нерівність, що виконуватиметься для m.

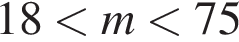
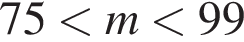
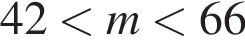
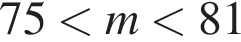
Знайдіть об’єм V частини циліндра, зображеної на малюнку. У відповіді вкажіть
![]()
Розв’яжіть рівняння 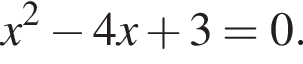
На малюнку зображено трикутник ABC, у якому ∠ ACB = 38°, ∠ AMN = 109°. Використовуючи дані малюнка, знайдіть градусну міру кута BAC.
На рисунку зображено графік функції
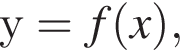 визначеної на проміжку [−3; 3]. Одна з наведених точок належить графіку функції
визначеної на проміжку [−3; 3]. Одна з наведених точок належить графіку функції  Укажіть цю точку.
Укажіть цю точку.
Спростіть вираз (a6)4: a2, ![]()
Площу будь-якого опуклого чотирикутника можна обчислювати за формулою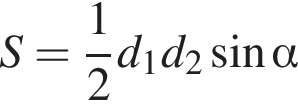 , де
, де![]() - Довжини його діагоналей, а
- Довжини його діагоналей, а![]() кут між ними. Обчисліть
кут між ними. Обчисліть![]() , якщо
, якщо .
.
Обчисліть 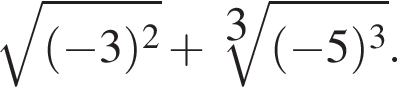
Які з наведених тверджень є правильними?
І. Бічні сторони будь-якої трапеції паралельні.
ІІ. Сума кутів, прилеглих до бічної сторони будь-якої трапеції, дорівнює 180°.
ІІІ. Сума протилежних кутів будь-якої трапеції дорівнює 180°.
Розв’яжіть систему рівнянь
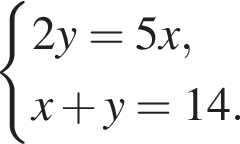
Для одержаного розв’язку (x0; у0) укажіть добуток x0 · y0.
Матеріальна точка рухається прямолінійно за законом 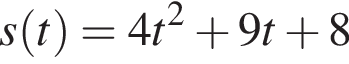 (шлях s вимірюється в метрах, час t — у секундах). Визначте швидкість (у м/с) цієї точки в момент часу t = 4 с.
(шлях s вимірюється в метрах, час t — у секундах). Визначте швидкість (у м/с) цієї точки в момент часу t = 4 с.
Розв'яжіть систему нерівностей: 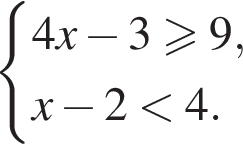


Знайти 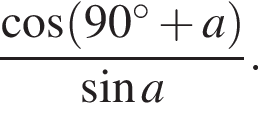

Два ребра прямокутного паралелепіпеда, що виходять з однієї вершини, дорівнюють 3 і 4. Площа поверхні цього паралелепіпеда дорівнює 94. Знайдіть третє ребро, що виходить із тієї ж вершини.
Визначте висоту будинку, ширина фасаду якого дорівнює 8 м, висота від фундаменту до даху дорівнює 4 м, а довжина схилу даху дорівнює 5 м.
На рисунках (1−3) зображено графіки функцій, визначених на відрізку [−4; 4].
Установіть відповідність між графіком функції (1−3) та властивістю (А−Д), що має ця функція.
А функція має лише один нуль
Б функція є непарною
В функція не має точок екстремуму
Г функція набуває лише додатних значень
Д графік функції проходить через точку (3; −2)
Установіть відповідність між виразом (1−3) та тотожно рівним йому виразом (А−Д), якщо а — довільне від’ємне число.
1. a0
2. ![]()
3. 
А 0
Б 2a
В a2
Г 1
Д −2a
У прямокутному трикутнику АВС катет АС = 12 см, гіпотенуза АВ = 20 см.
Установіть відповідність між відрізком (1–3) та його довжиною (А–Д).
1 катет BC
2 радіус кола, описаного навколо трикутника АВС
3 висота трикутника АВС, проведена до гіпотенузи АВ
А 19,2 см
Б 9,6 см
В 10 см
Г 8 см
Д 16 см
Які з наведених тверджень є правильними?
I.Чи вірно, що прямі a і b перетинаються, якщо кожна з цих прямих перетинається з прямою с?
II. Чи вірно, що прямі a та b перетинаються, якщо пряма b перетинається з прямою c, а пряма c перетинається з прямою a?
III. Чи вірно, що прямі a та b перетинаються, якщо пряма a перетинає площину, паралельну до прямої b?
Одна таблетка лекарства весит 20 мг и содержит 5% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,4 мг активного вещества на каждый килограмм веса в сутки.
1. Сколько таблеток этого лекарства следует дать ребёнку в возрасте четырёх месяцев и весом 5 кг в течение суток?
2. В какой-то момент врач прописал новые таблетки, которые содержат не 5% активного вещества, а 17,5%. Сколько таблеток в таком случае следует дать ребенку в течении суток?
У довільній трапеції ABCD середня лінія MN дорівнює 10 см, а відрізок LK, що з'єднує середини діагоналей, дорівнює 3 см. Висота трапеції ABCD дорівнює 6 см.
1. Вычислить отрезок AD.
2. Вычислить высоту трапеции AMND.
У прямокутній системі координат у просторі задано вектор 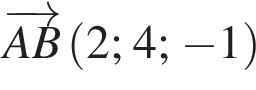 і точку
і точку 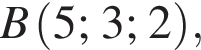 точка О — початок координат.
точка О — початок координат.
1. Визначте абсцису y точки 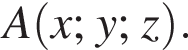
2. Обчисліть скалярний добуток 
В арифметичній прогресії (an) другий член дорівнює 18, а різниця прогресії d = 2,4.
1. Определите первый член этой прогрессии.
2. Знайдіть суму перших 7 членів прогресії.
Дві фабрики випускають однакові стекла для автомобільних фар. Перша фабрика випускає 45% цього скла, друга — 55%. Перша фабрика випускає 3% бракованого скла, а друга — 1%. Знайдіть ймовірність того, що випадково куплене в магазині скло виявиться бракованим.
У майстерні мали виготовити 240 стільців за п днів, причому щодня планували виробляти однакову кількість стільців. Однак, на прохання замовника, завдання виконали на 2 дні раніше запланованого терміну. Для цього довелося денну норму виготовлення збільшити на 4 стільці. Визначте n.
Спростіть вираз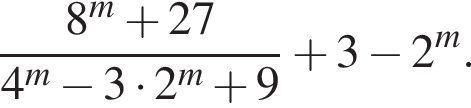
Розв'яжіть рівняння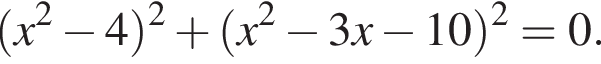 У відповіді напишіть суму всіх його дійсних коренів.
У відповіді напишіть суму всіх його дійсних коренів.
Сколько различных аккордов, содержащих 3 звука, можно взять на 13 клавишах одной октавы?
| x | y |
|---|---|
| 1 | |
| 2 | |
| 4 |
Задано функцію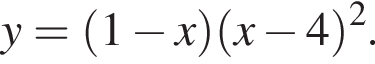
1. Знайдіть первісну функції![]() , графік якої дотикається прямої
, графік якої дотикається прямої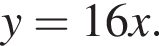
2. Для наведених у таблиці значень аргументів х визначте відповідні їм значення для функції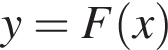 (Див. таблицю).
(Див. таблицю).
3. Визначте нулі функції F .
4. Визначте точки екстремуму.
5. Визначте проміжки зростання та спадання.
6. Побудуйте ескіз графіка функції F .
Сторона основи правильної трикутної піраміди дорівнює 3. Бічні ребра нахилені до основи під кутом α.
1. Зобразіть на малюнку цю піраміду та кут α.
2. Визначте висоту піраміди.
3. Знайдіть об'єм піраміди.
Відповідно до умови завдання 31 (№ 3514) сторона основи правильної чотирикутної піраміди дорівнює 3. Бічні ребра нахилені до основи під кутом α.
1. Зобразіть на малюнку цю піраміду та побудуйте лінійний кут двогранного кута при бічному ребрі.
2. Знайдіть цей кут.
Доведіть нерівність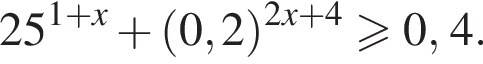
Задана система уравнений
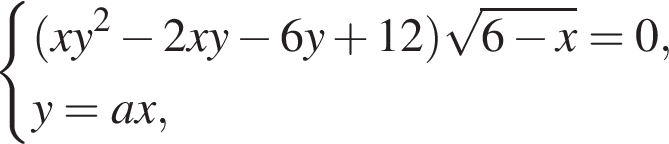
1. Решите систему уравнений при ![]()
2. Найдите все значения параметра a, при каждом из которых система уравнений имеет ровно три различных решения.

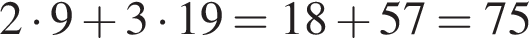 гривен, а если самые дорогие, то
гривен, а если самые дорогие, то  гривен. Значит
гривен. Значит 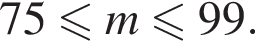
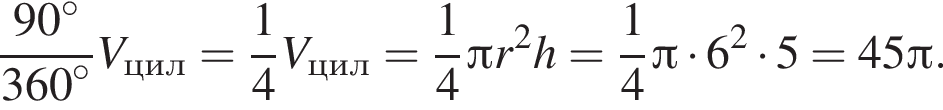
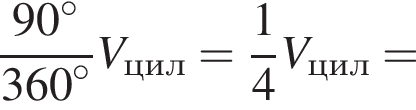
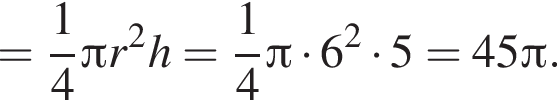
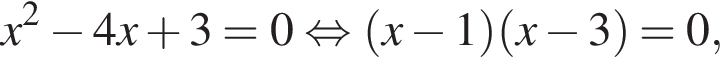
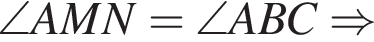
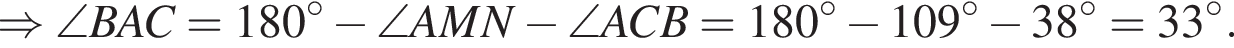
 отличается от
отличается от 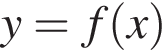 симметрией относительно горизонтальной оси. Поэтому можно рассмотреть точки, симметричные данным, и изучить, какая из них попадет на график
симметрией относительно горизонтальной оси. Поэтому можно рассмотреть точки, симметричные данным, и изучить, какая из них попадет на график 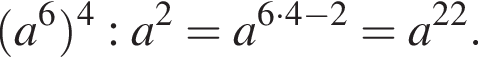
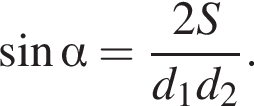
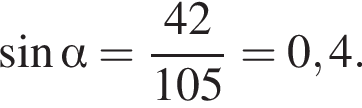
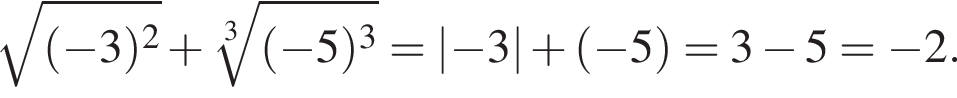
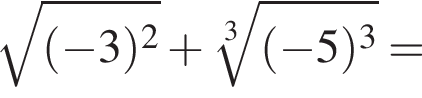
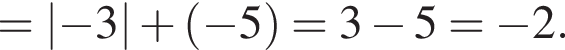
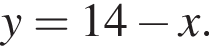 Подставляя в первое уравнение, получаем
Подставляя в первое уравнение, получаем 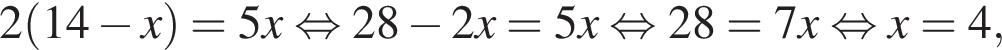

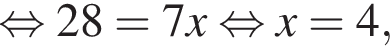
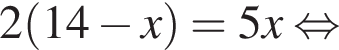

 и
и 
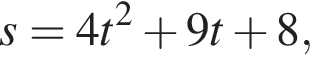 то
то  и
и 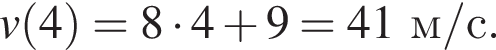
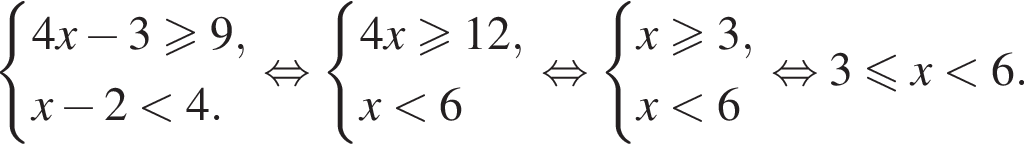
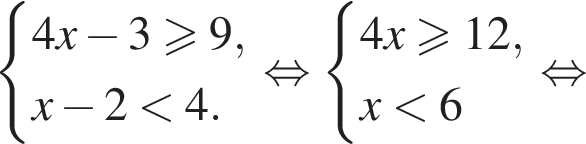
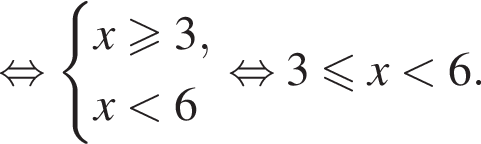
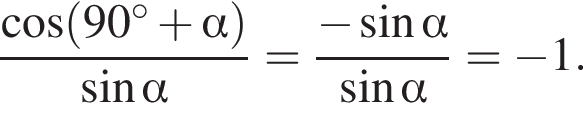
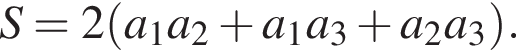 Пусть неизвестное ребро равно x. Подставляя известные величины из условия, получаем:
Пусть неизвестное ребро равно x. Подставляя известные величины из условия, получаем:

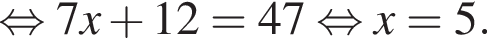

 Таким образом, 1 — Г.
Таким образом, 1 — Г. По определению модуля:
По определению модуля: 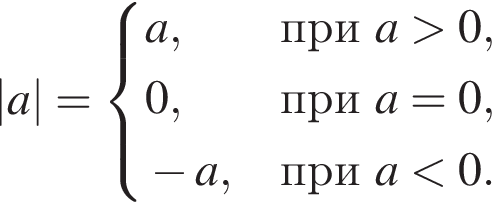
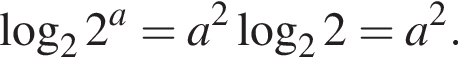 Таким образом, 3 — B.
Таким образом, 3 — B.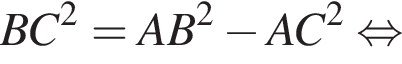

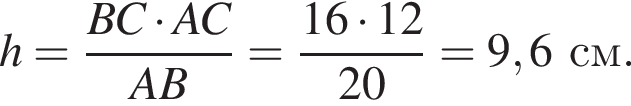 Ответ — Б.
Ответ — Б.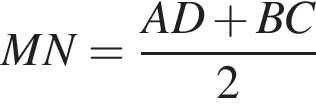 и
и 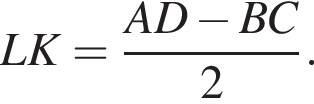 Составим и решим систему уравнений:
Составим и решим систему уравнений: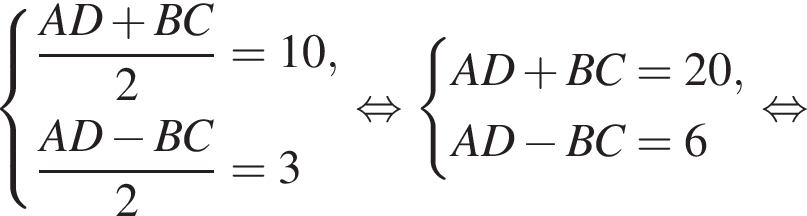
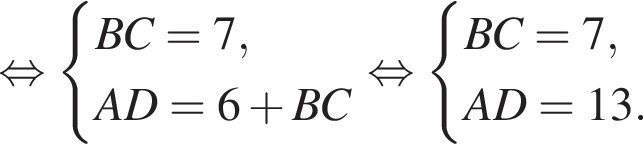
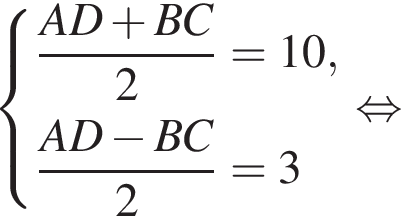
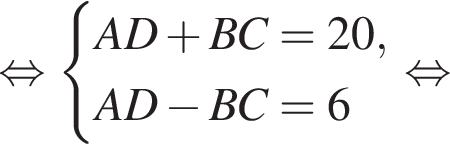
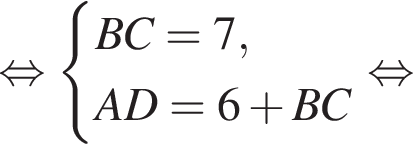
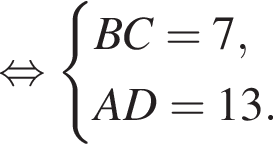
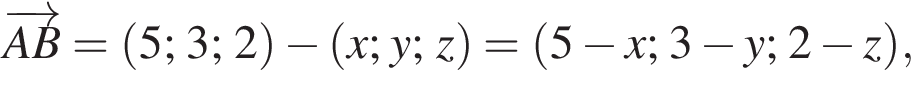
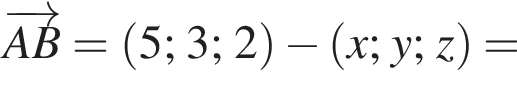
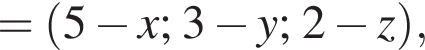
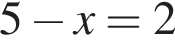 и
и  и
и 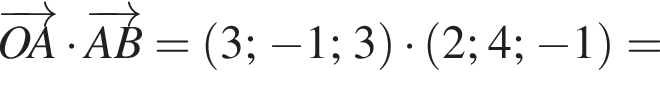

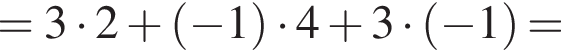

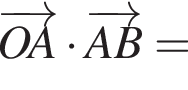

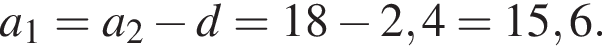 Обчислимо суму перших шести членів арифметичної прогресії:
Обчислимо суму перших шести членів арифметичної прогресії: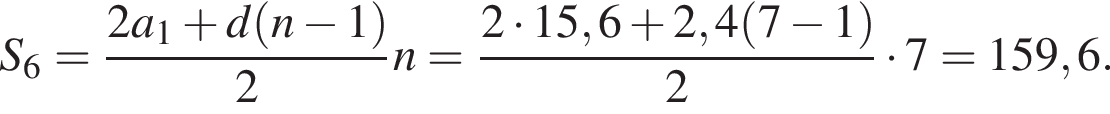
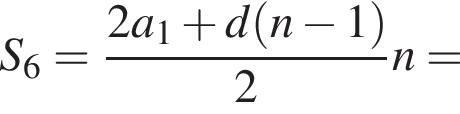
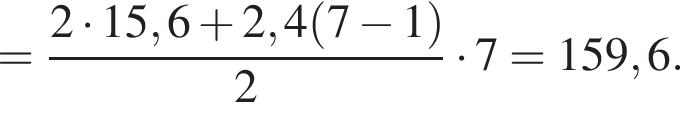
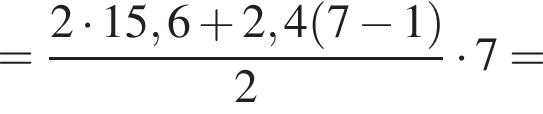

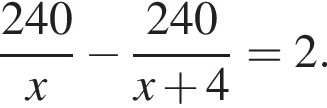
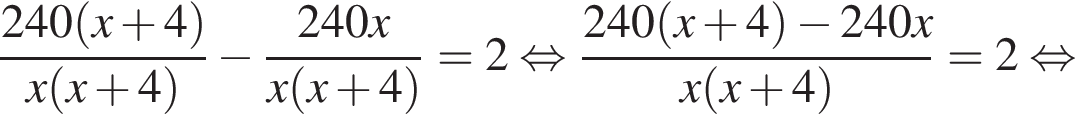
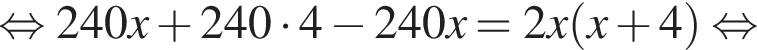


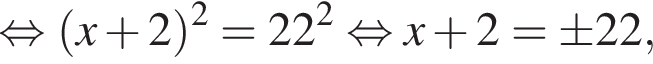
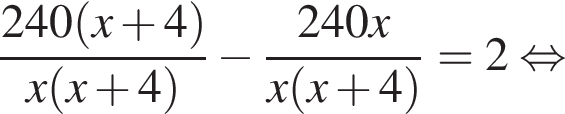
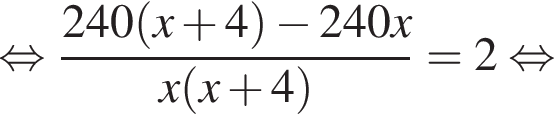
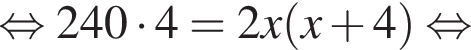
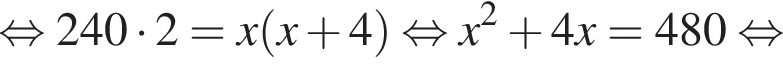
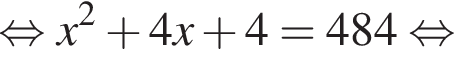

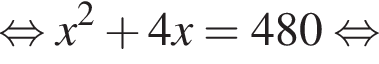
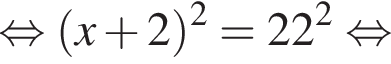
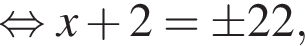
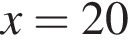 и
и 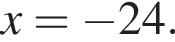 Второй случай невозможен. Итак,
Второй случай невозможен. Итак,  а срок по плану составлял
а срок по плану составлял 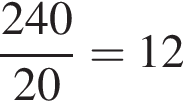 дней.
дней.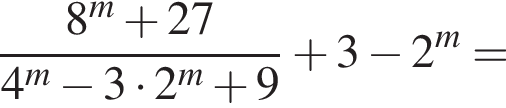
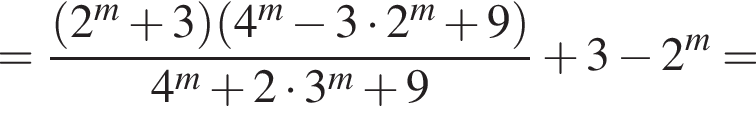
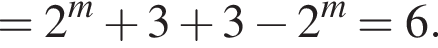
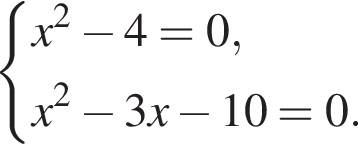
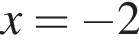 или
или 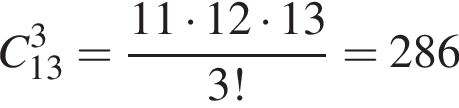 различных аккордов.
различных аккордов.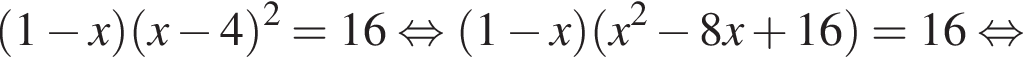
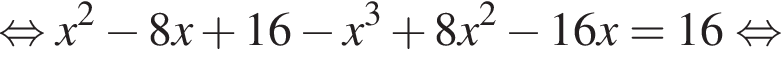
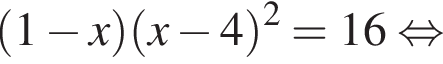
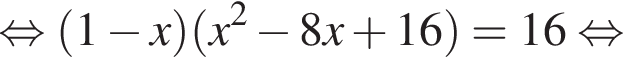
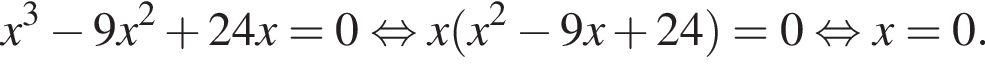
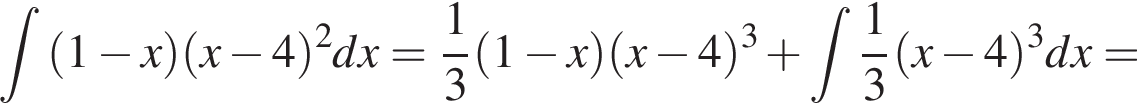
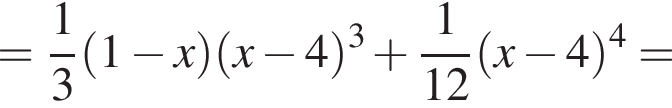
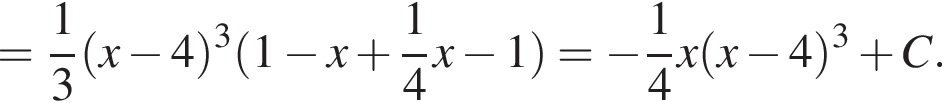
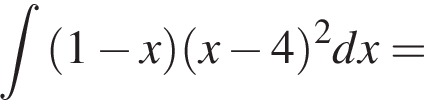
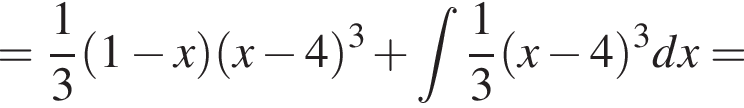
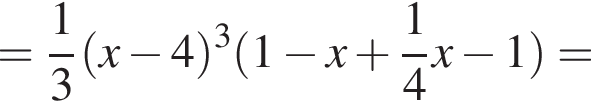
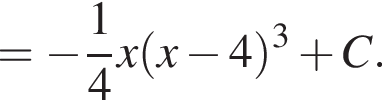

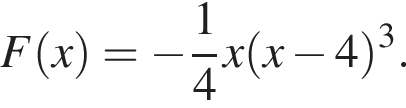
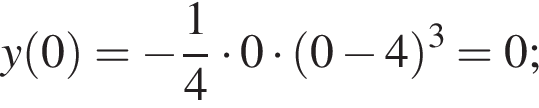
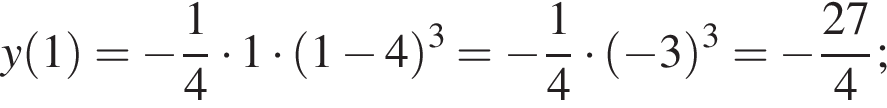
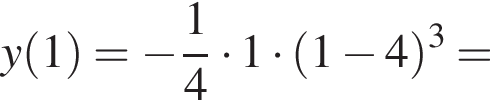
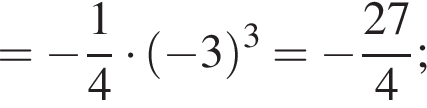
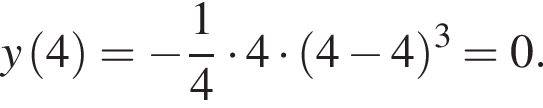
 при
при 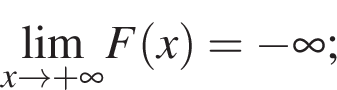
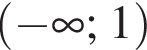 производная положительна, следовательно, функция возрастает. На
производная положительна, следовательно, функция возрастает. На  производная отрицательна, следовательно, функция убывает.
производная отрицательна, следовательно, функция убывает.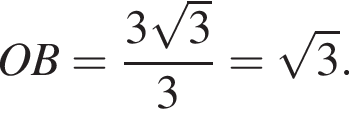 Выразим высоту SO пирамиды из прямоугольного треугольника SOB, получим:
Выразим высоту SO пирамиды из прямоугольного треугольника SOB, получим: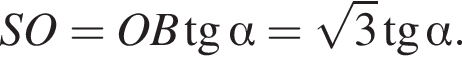
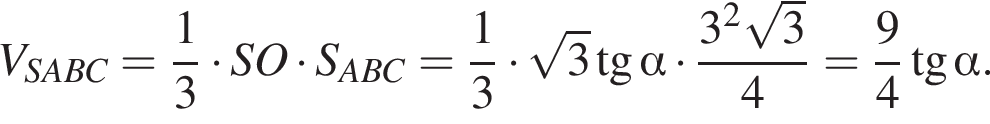
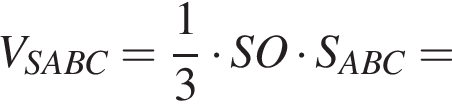
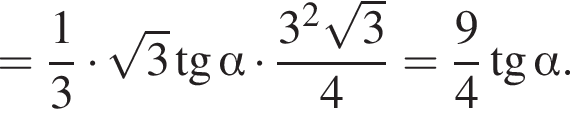
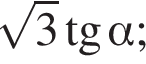 3)
3)  то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
то есть прямые AK и CK суть перпендикуляры к ребру двугранного угла между плоскостями SBA и SBC, а потому угол AKC — линейный угол двугранного угла при боковом ребре. Обозначим его δ.
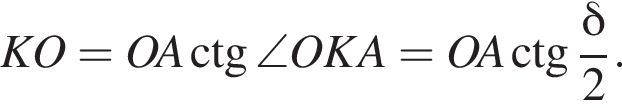
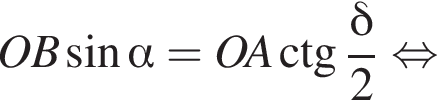
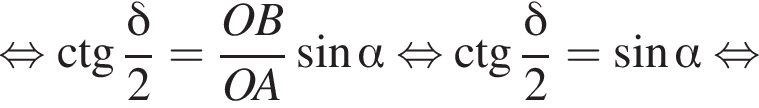
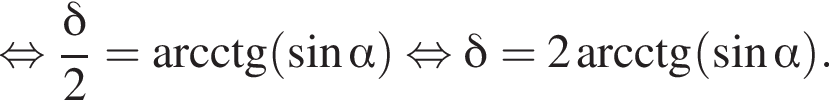
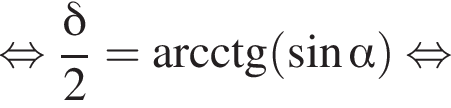

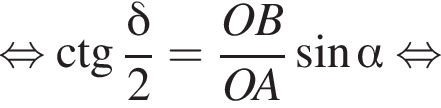
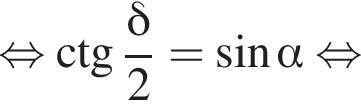
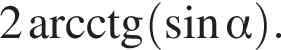
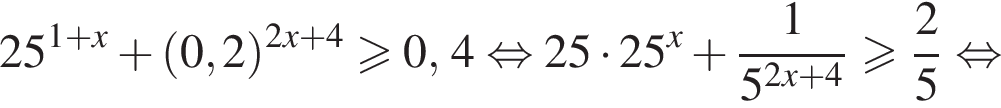
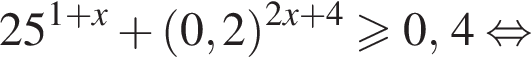
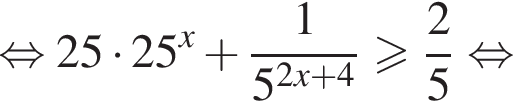
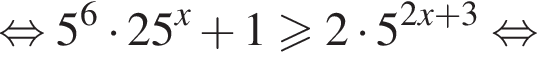
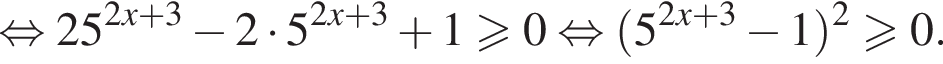
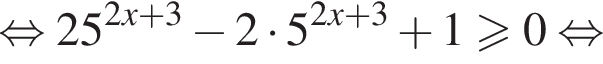
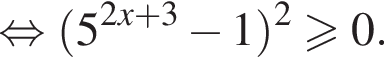

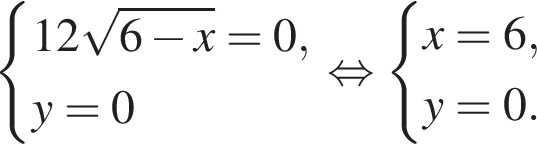
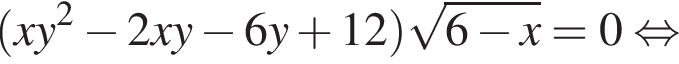
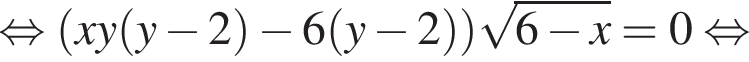
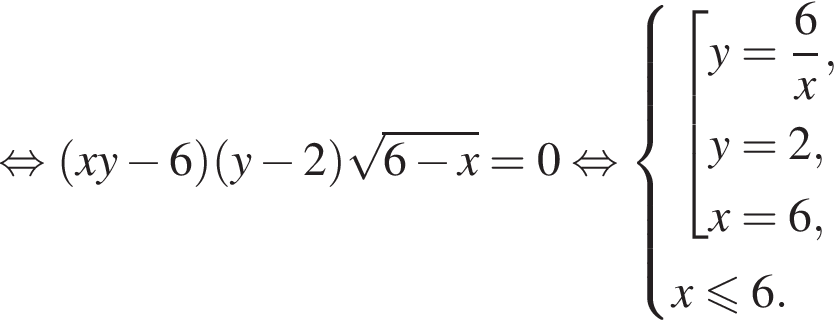
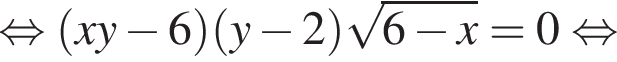
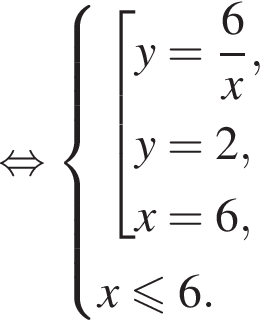
 три различных точки пересечения на области
три различных точки пересечения на области 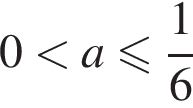 два решения, при
два решения, при 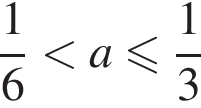 три решения, при
три решения, при 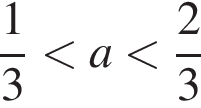 четыре решения, при
четыре решения, при