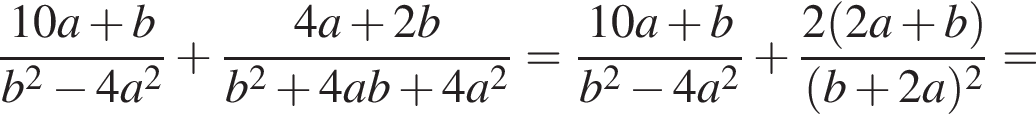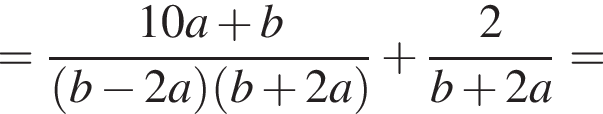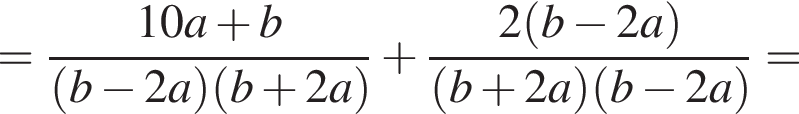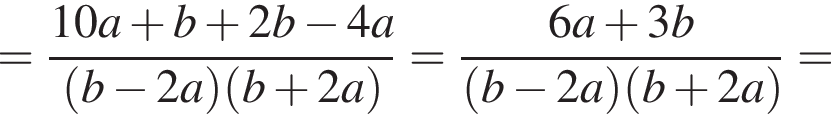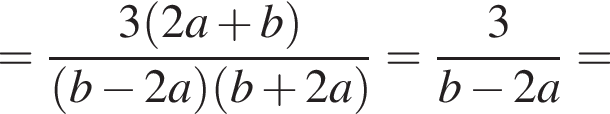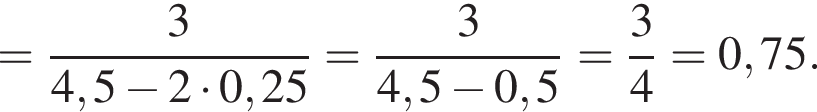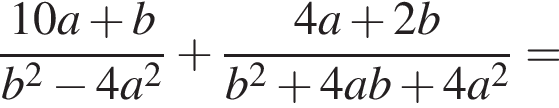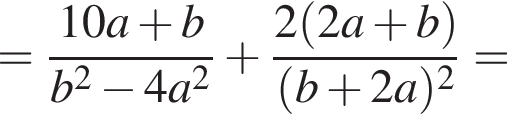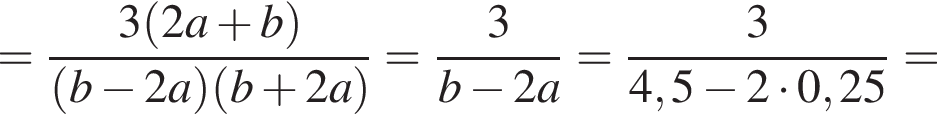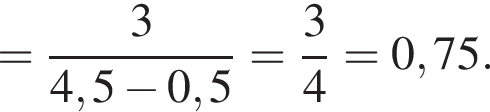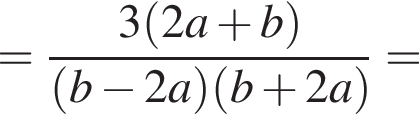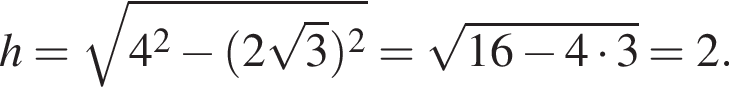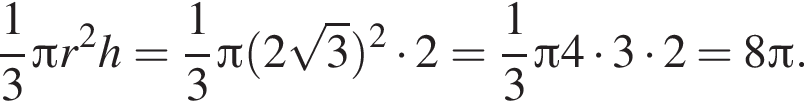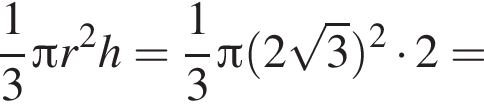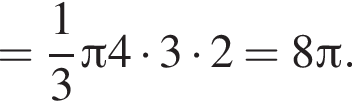1. Тип 7 № 613 

Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
Перетворення виразів. Прості перетворення
i
Знайти 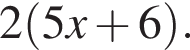
А) 

Б) 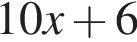
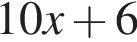
В) 
Г) 

Д) 
Решение. Чтобы умножить одночлен на многочлен, нужно каждое слагаемое в скобках умножить на этот одночлен. Получаем:
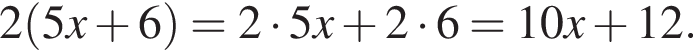
Правильный ответ указан под номером 1.
Ответ: 1
613
1
Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
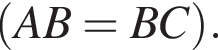 Визначте градусну міру кута BAC, якщо
Визначте градусну міру кута BAC, якщо 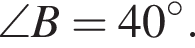
 По теореме о сумме углов треугольника получаем:
По теореме о сумме углов треугольника получаем: 

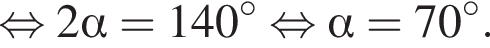
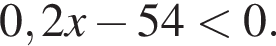
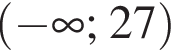
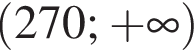
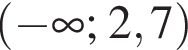
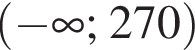
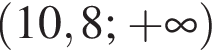
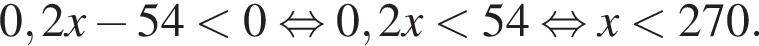
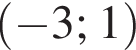 лежит на нем, а остальные не лежат (точки на рисунке выделены красным, подходящая точка — синим.) НУЖЕН РИСУНОК!
лежит на нем, а остальные не лежат (точки на рисунке выделены красным, подходящая точка — синим.) НУЖЕН РИСУНОК!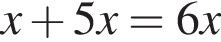 яблок, тогда Петр собрал
яблок, тогда Петр собрал 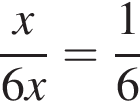 из них.
из них.
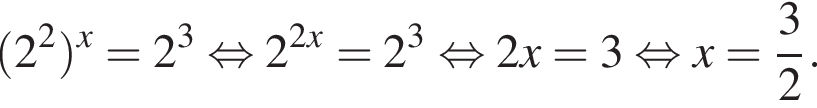

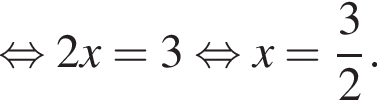
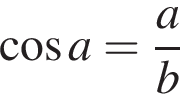
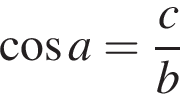

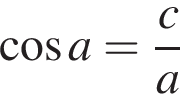
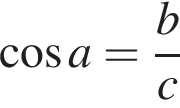
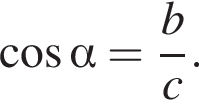
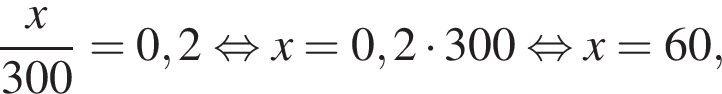

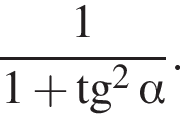
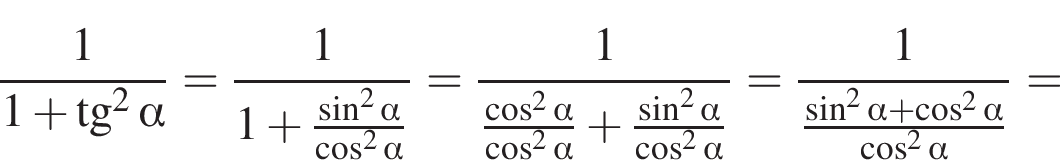
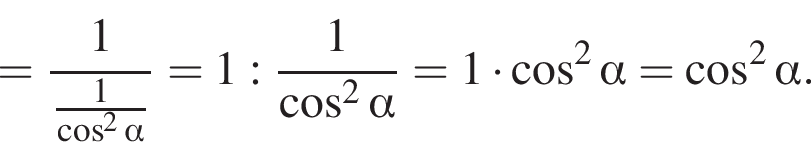
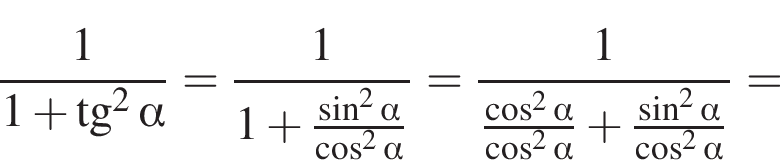
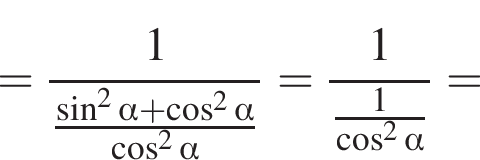
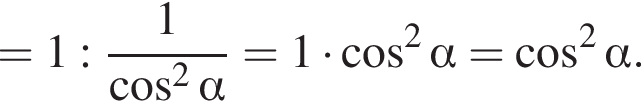
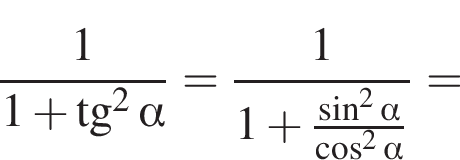
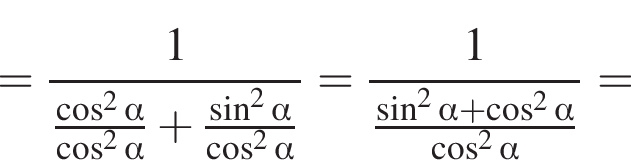
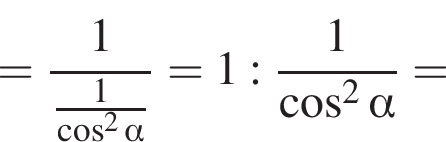
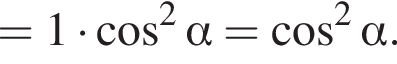
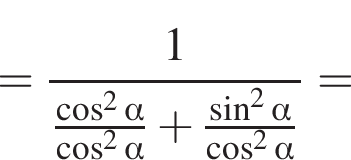
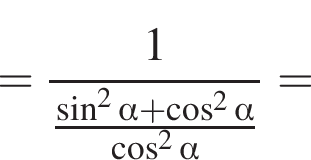
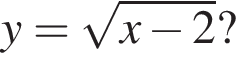
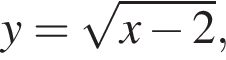 тогда
тогда  то есть на графике должна лежать точка (2; 0). Кроме того, при
то есть на графике должна лежать точка (2; 0). Кроме того, при 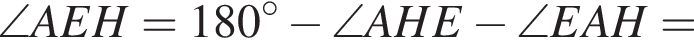
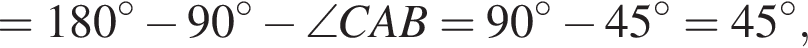
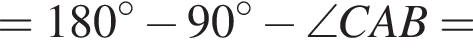

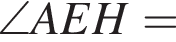

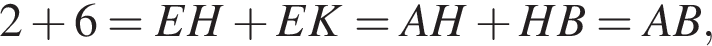
 см
см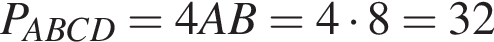 см.
см.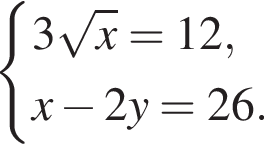

 Подставляя полученное значение во второе уравнение, находим
Подставляя полученное значение во второе уравнение, находим 
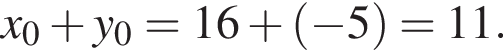
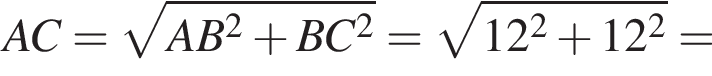
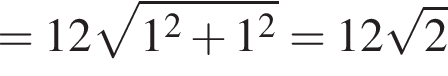
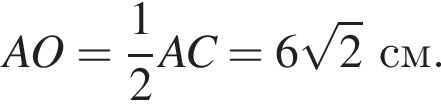
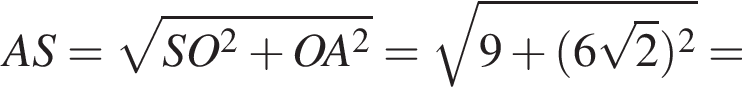
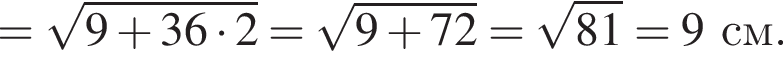
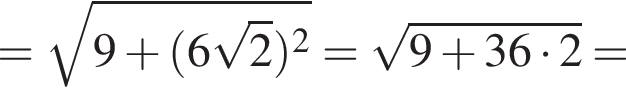
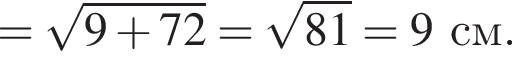
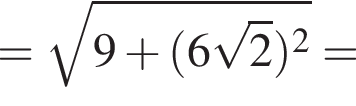
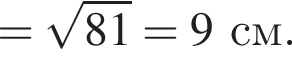
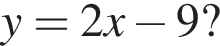
 является возрастающей, поскольку если
является возрастающей, поскольку если 

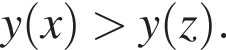 Это автоматически запрещает варианты В и Г. Кроме того, поскольку
Это автоматически запрещает варианты В и Г. Кроме того, поскольку 
 и эти значения не равны и не отличаются знаком, варианты А и Б так же отпадают.
и эти значения не равны и не отличаются знаком, варианты А и Б так же отпадают.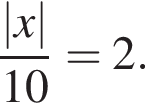
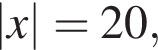 откуда
откуда 
 згортають таким чином, щоб отримати циліндричну трубу (див. лівий і правий рисунки). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнюе 20 см. Виберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварювання знехтуйте.
згортають таким чином, щоб отримати циліндричну трубу (див. лівий і правий рисунки). Краї AB і CD зварюють між собою без накладання одного краю на інший. Обчисліть площу бічної поверхні отриманого циліндра (труби), якщо діаметр його основи дорівнюе 20 см. Виберіть відповідь, найближчу до точної. Товщиною листа заліза та швом від зварювання знехтуйте.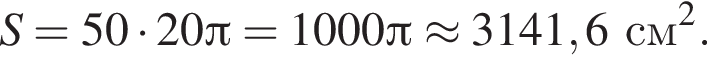
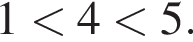 Взяв логарифмы по основанию 5 ото всех чисел в этом двойном неравенстве и пользуясь возрастанием логарифмической функции с основанием, большим 1, получаем, что
Взяв логарифмы по основанию 5 ото всех чисел в этом двойном неравенстве и пользуясь возрастанием логарифмической функции с основанием, большим 1, получаем, что 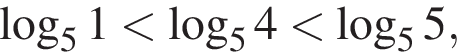 то есть
то есть 
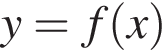 у точці з абсцисою
у точці з абсцисою  якщо
якщо 
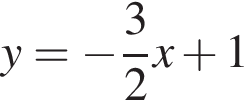
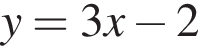

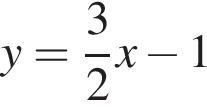
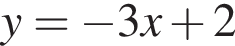
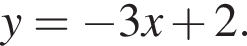
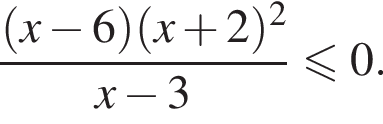
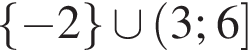
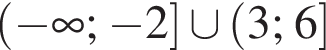
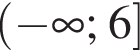

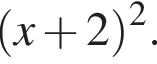 Расставляя остальные знаки, получаем, что функция положительна при
Расставляя остальные знаки, получаем, что функция положительна при  и
и 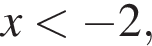 а отрицательна при
а отрицательна при 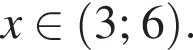 Добавляя сюда точки
Добавляя сюда точки 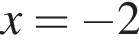 и
и 
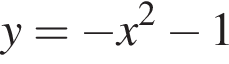
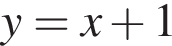
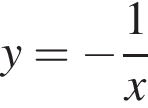
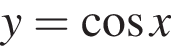
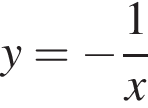 при положительных x принимает отрицательные значения, то есть ее график не проходит через первую четверть. Такой вариант остался один (А).
при положительных x принимает отрицательные значения, то есть ее график не проходит через первую четверть. Такой вариант остался один (А). 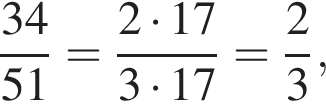 у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.
у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.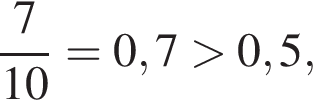
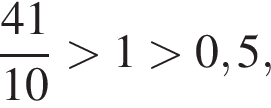
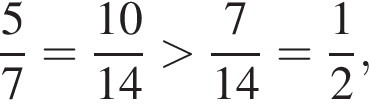
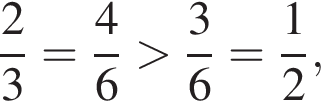
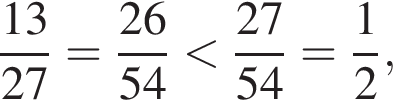
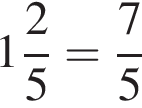 будет дробь
будет дробь 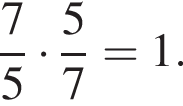
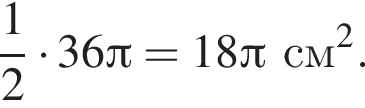
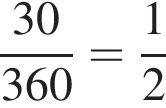 часть площади круга радиуса 12, то есть
часть площади круга радиуса 12, то есть 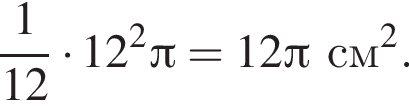
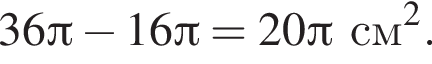
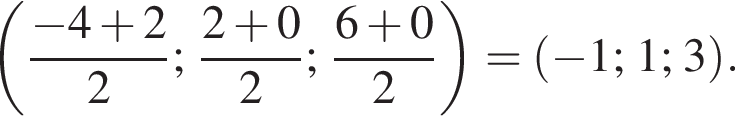

 По условию
По условию  откуда
откуда 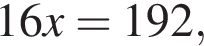
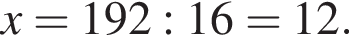
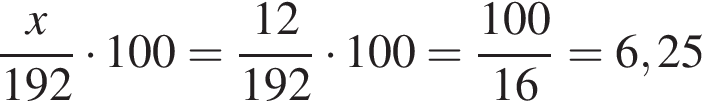
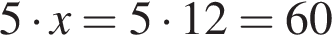 штук.
штук.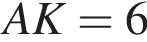 см,
см, см,
см, см.
см.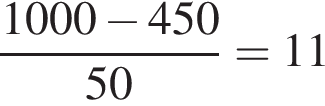 раз увеличивать расстояние. То есть на 12 тренировке он впервые проплывет 1000 метров. После этого он еще
раз увеличивать расстояние. То есть на 12 тренировке он впервые проплывет 1000 метров. После этого он еще 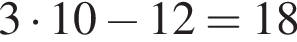 раз проплывет по 1000 метров. За первые же 12 тренировок он проплывет
раз проплывет по 1000 метров. За первые же 12 тренировок он проплывет 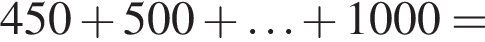
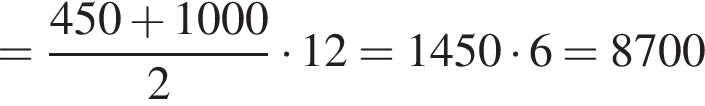
 метров, то есть
метров, то есть 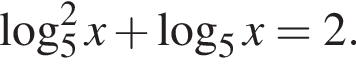 Якщо рівняння мас один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть і̄хню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100.
Якщо рівняння мас один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть і̄хню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100.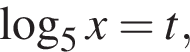 уравнение примет вид
уравнение примет вид  Решим его.
Решим его. 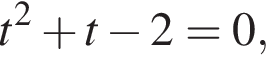
 Уравнение
Уравнение 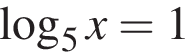 имеет корень
имеет корень 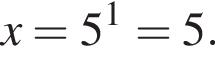 Уравнение
Уравнение 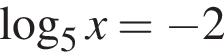 имеет корень
имеет корень 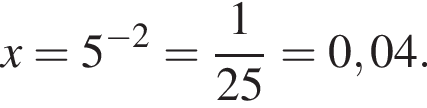
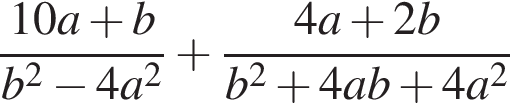
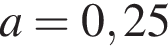 i
i