1. Тип 9 № 953 

Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
Перетворення та обчислення різних виразів. Обчислення значень виразів
i
Якщо 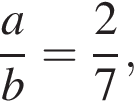 то
то ![]() рівний?
рівний?
А) 
Б) 
В) 
Г) 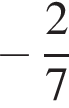
Д) 
Решение. Так как ![]() и
и ![]() — обратные числа, получаем:
— обратные числа, получаем: 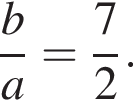
Правильный ответ указан под номером 2.
Ответ: 2
953
2
Классификатор алгебры: 1\.2\. Преобразования целых буквенных выражений
 с направлением на восток. Угол между дорогами тогда равен
с направлением на восток. Угол между дорогами тогда равен 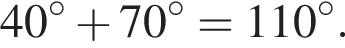
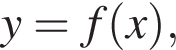 визначеної на проміжку [−4; 5]. Точка (х0; −2) належить графіку цієї функції. Визначте абсцису x0 цієї точки.
визначеної на проміжку [−4; 5]. Точка (х0; −2) належить графіку цієї функції. Визначте абсцису x0 цієї точки. — на две клетки ниже горизонтальной оси. Она пересечет график функции в одной точке, координаты которой будут (−3; −2). Поэтому абсцисса ее равна −3.
— на две клетки ниже горизонтальной оси. Она пересечет график функции в одной точке, координаты которой будут (−3; −2). Поэтому абсцисса ее равна −3.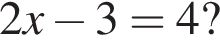
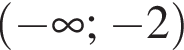

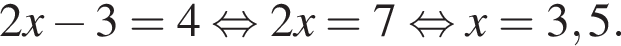
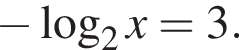
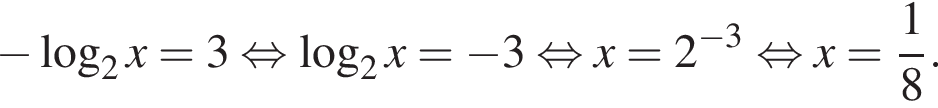
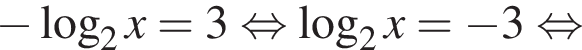
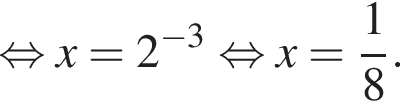
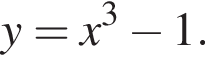
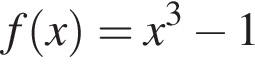 в точке
в точке 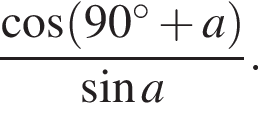

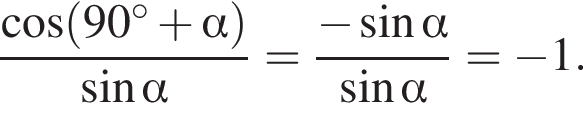
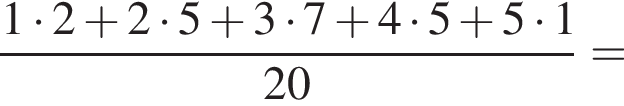
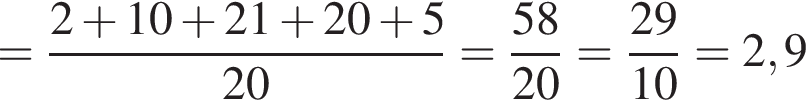
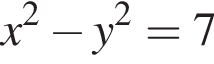 i
i 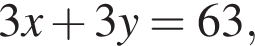 то
то 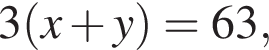 откуда
откуда 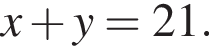 Теперь из первого уравнения получаем
Теперь из первого уравнения получаем 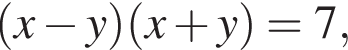 откуда
откуда 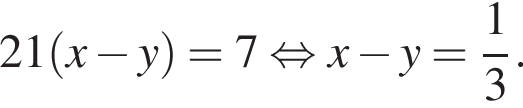
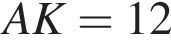 см,
см,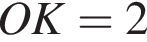 см,
см,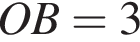 см.
см. как вертикальные,
как вертикальные,  как накрест лежащие. Значит,
как накрест лежащие. Значит, 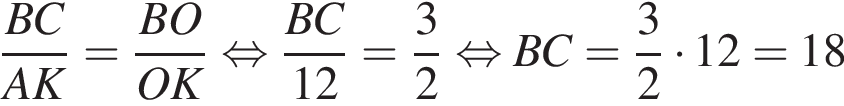
 то
то 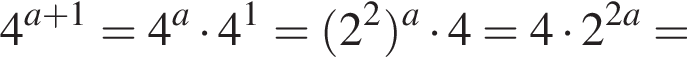
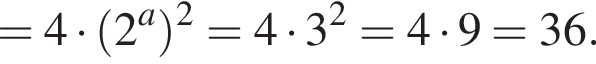
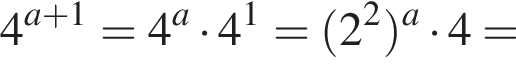
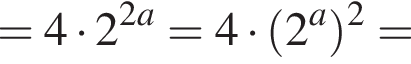
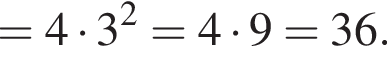

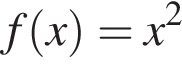
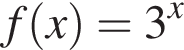
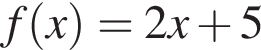

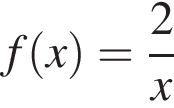
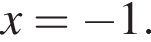 Из этих функций такой будет только последняя. И действительно, при всех x
Из этих функций такой будет только последняя. И действительно, при всех x 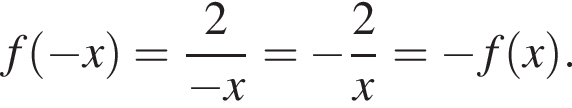
 см3
см3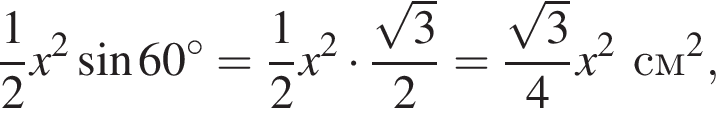
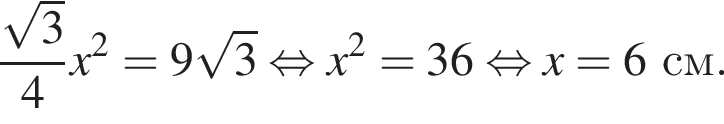
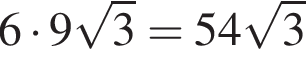 см3.
см3.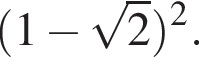
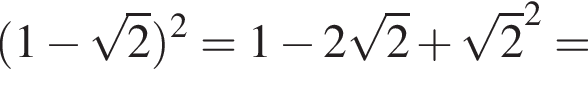


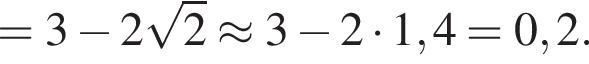
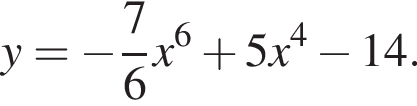
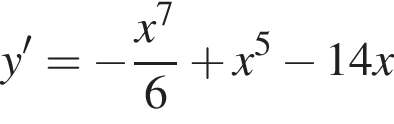
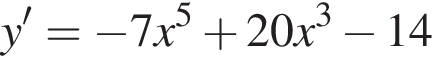
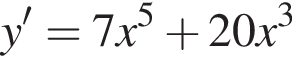
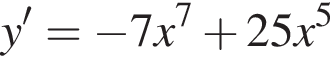
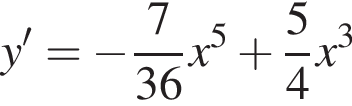
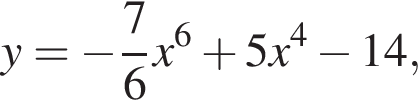 используя правило нахождения производной суммы функций:
используя правило нахождения производной суммы функций: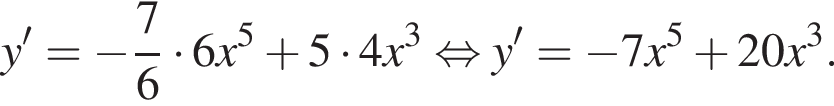
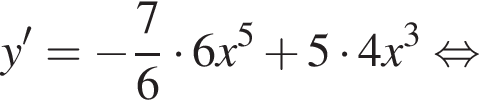
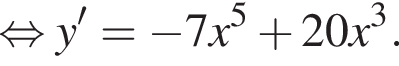
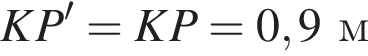 i
i 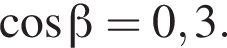 Наявністю заднього бампера автомобіля знехтуйте.
Наявністю заднього бампера автомобіля знехтуйте.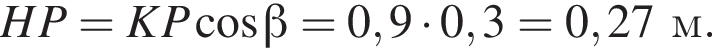
 от P. Поэтому расстояние до стены должно быть не менее 0,63 м. Минимально подходящее расстояние из предложенных — 0,7 м.
от P. Поэтому расстояние до стены должно быть не менее 0,63 м. Минимально подходящее расстояние из предложенных — 0,7 м.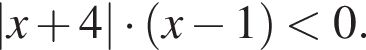

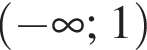

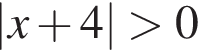 при всех
при всех 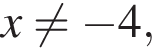 поэтому оно не влияет на знак. Решив неравенство
поэтому оно не влияет на знак. Решив неравенство 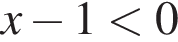 получим
получим 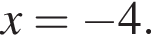 Окончательно получаем ответ:
Окончательно получаем ответ: 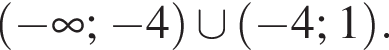
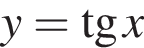
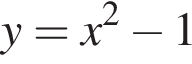
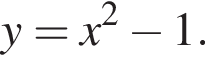 Таким образом, 2 — Б.
Таким образом, 2 — Б. 
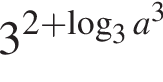
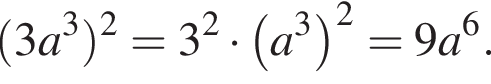 Ответ — А.
Ответ — А. Ответ — Д.
Ответ — Д.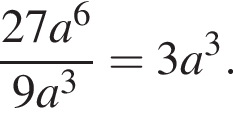 Ответ — Г.
Ответ — Г.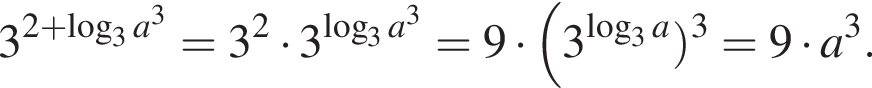
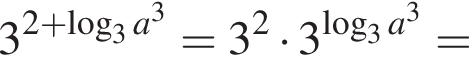
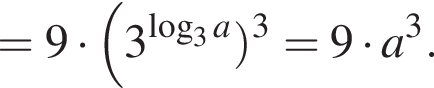
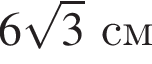
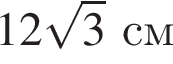
 тогда
тогда 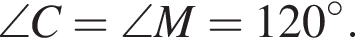 Большей диагональю ромба является KD. Применим теорему косинусов в треугольнике CKD:
Большей диагональю ромба является KD. Применим теорему косинусов в треугольнике CKD: 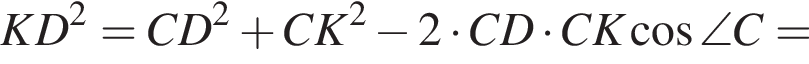
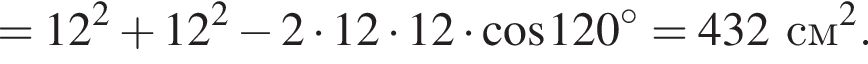
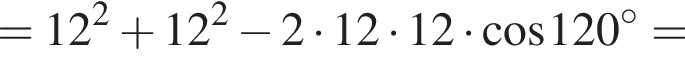
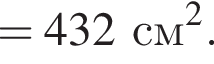
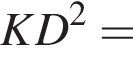
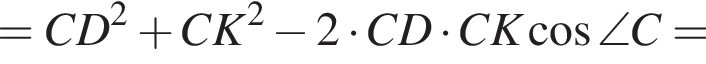
 Итак, 2 — Г.
Итак, 2 — Г.  Имеем:
Имеем:
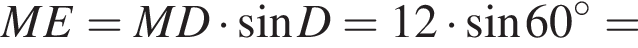
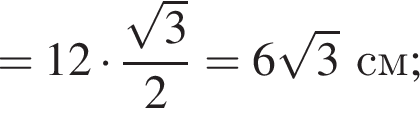

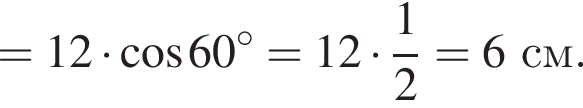

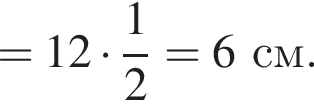

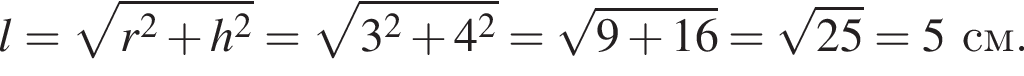
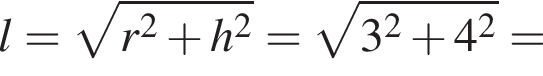

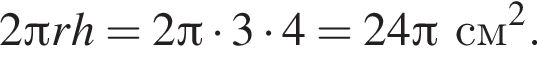 Площадь полной поверхности цилиндра тогда равна
Площадь полной поверхности цилиндра тогда равна 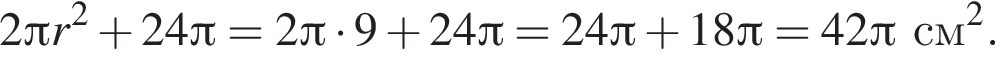
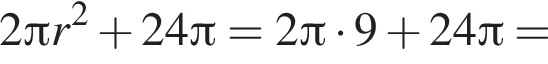
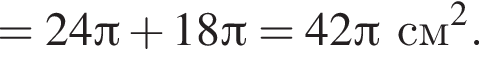
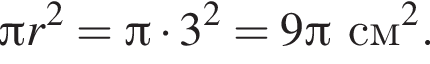 Площадь боковой поверхности конуса равна
Площадь боковой поверхности конуса равна 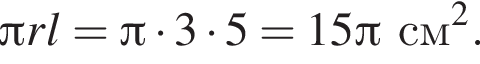
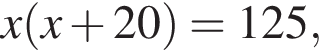 откуда
откуда 
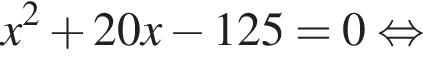
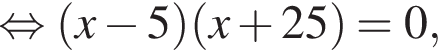
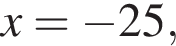 что невозможно. Значит в каждом ряду по
что невозможно. Значит в каждом ряду по 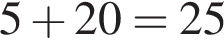 кустов. Из 25 кустов в первом ряду получили повреждения
кустов. Из 25 кустов в первом ряду получили повреждения 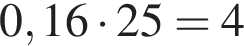 куста, а остальные
куста, а остальные 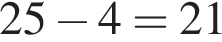 куст перезимовали без повреждений.
куст перезимовали без повреждений. По условию
По условию  откуда
откуда 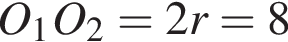 см
см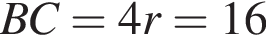 см.
см.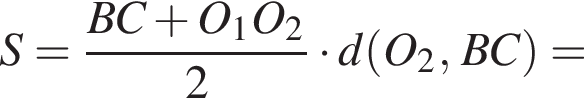
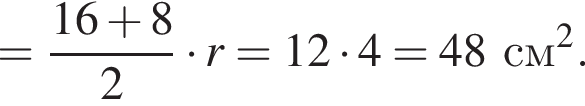
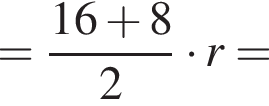

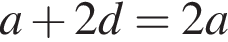 и
и 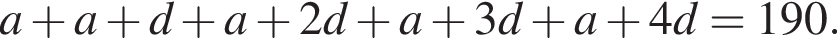

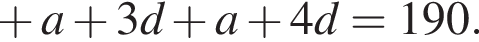
 второе
второе 

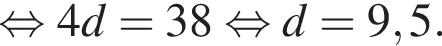
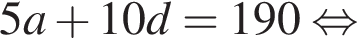
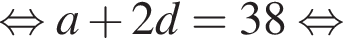
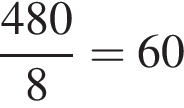 страниц, то есть ее скорость в
страниц, то есть ее скорость в 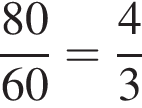 раза выше. Значит, пока она отредактирует 320 страниц, Максим отредактирует количество страниц, равное
раза выше. Значит, пока она отредактирует 320 страниц, Максим отредактирует количество страниц, равное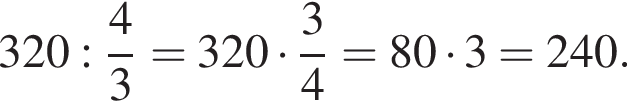
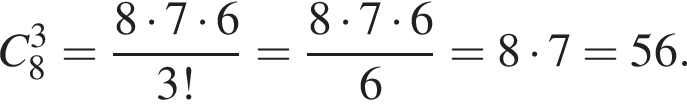
 способа.
способа.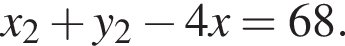 Визначте довжину сторони BC, якщо
Визначте довжину сторони BC, якщо 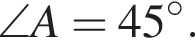
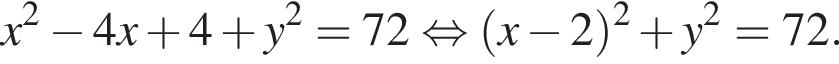
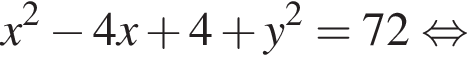
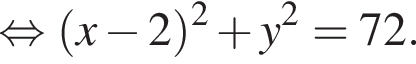
 По теореме синусов:
По теореме синусов: 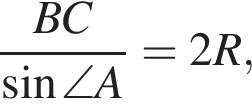
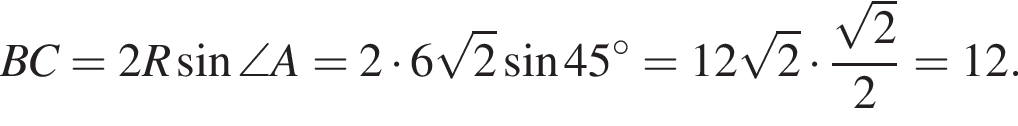
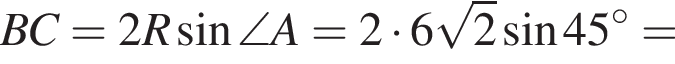
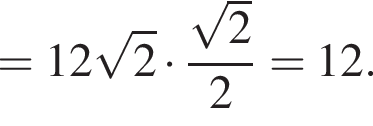

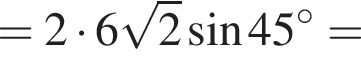
 i
i 
 и
и 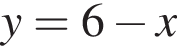 представлены на рисунке. Оба они стандартные — ветвь параболы, повернутая на 90°, и прямая. Найдем точки их пересечения. Решим уравнение
представлены на рисунке. Оба они стандартные — ветвь параболы, повернутая на 90°, и прямая. Найдем точки их пересечения. Решим уравнение 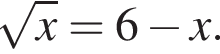 Ясно, что при
Ясно, что при 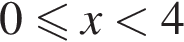 график
график 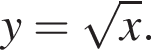 Значит, ограниченная ими площадь равна
Значит, ограниченная ими площадь равна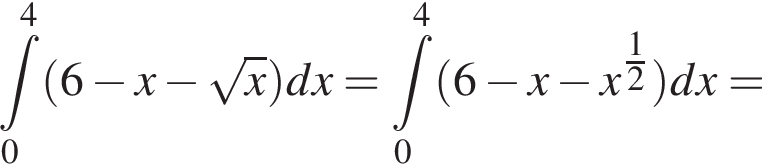
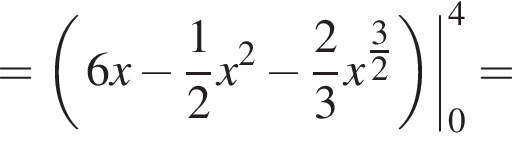
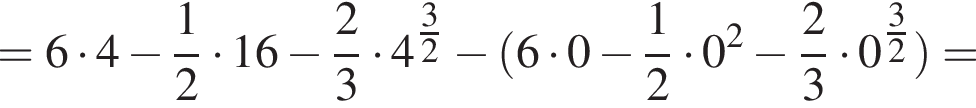
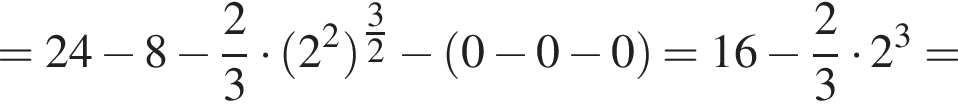
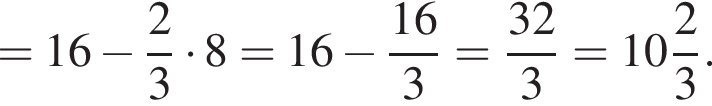
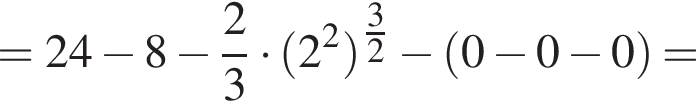
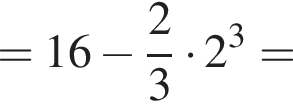
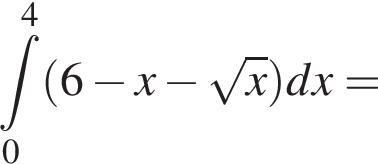
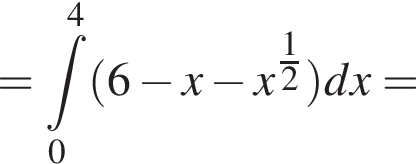
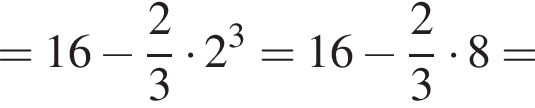
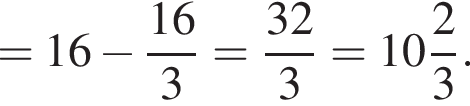
 4)
4) 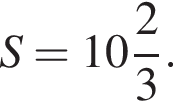
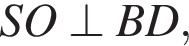 поскольку диагонали квадрата перпендикулярны. Следовательно
поскольку диагонали квадрата перпендикулярны. Следовательно 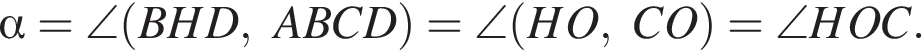
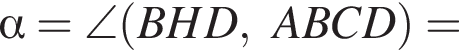

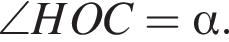 Тогда
Тогда  получаем:
получаем: 

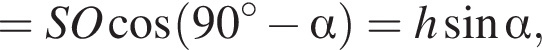
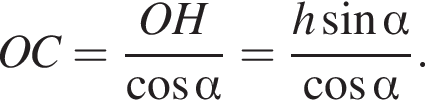
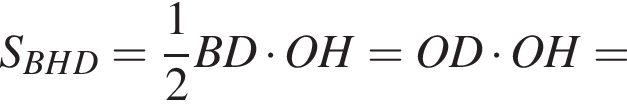
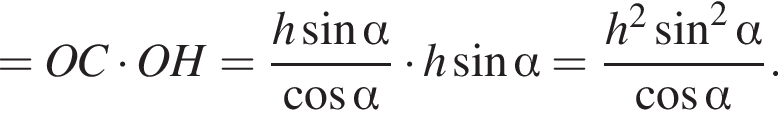
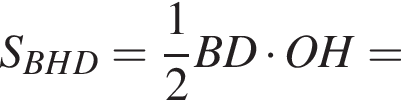

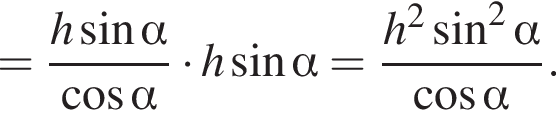
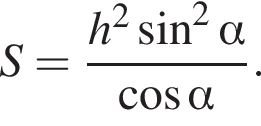
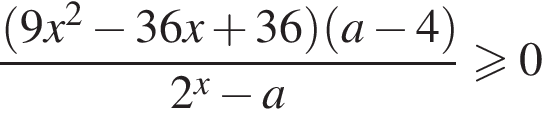
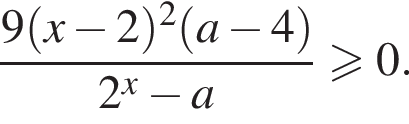
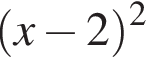 положительно кроме
положительно кроме 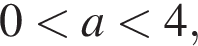 то
то 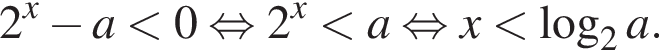
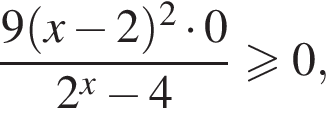
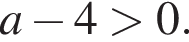 По-прежнему,
По-прежнему, 
 то
то  то
то 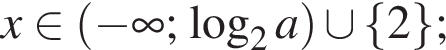
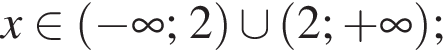
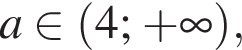 то
то 