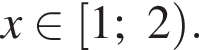1. Тип 7 № 919 

Классификатор алгебры: 1\.3\. Преобразования алгебраических дробей
Перетворення виразів. Прості перетворення
i
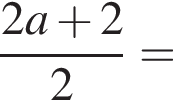
А) a + 2
Б) 2a + 1
В) a + 1
Г) 2a
Д) a
Решение. Упростим:
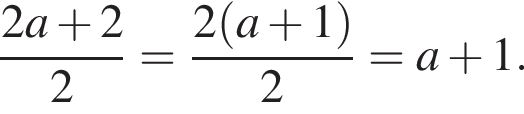
Правильный ответ указан под номером 3.
Ответ: 3
919
3
Классификатор алгебры: 1\.3\. Преобразования алгебраических дробей
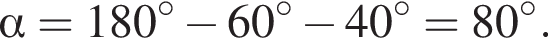
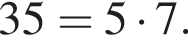
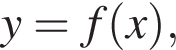 визначеної на проміжку [−4; 6]. Укажіть найбільше значення функції f на цьому проміжку.
визначеної на проміжку [−4; 6]. Укажіть найбільше значення функції f на цьому проміжку.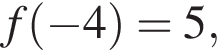 а все остальные точки графика находятся ниже этого уровня. Значит, ответ 5.
а все остальные точки графика находятся ниже этого уровня. Значит, ответ 5.
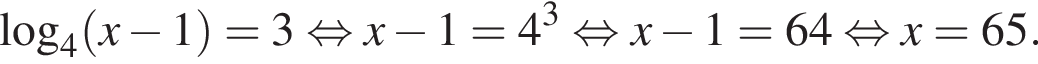

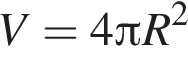
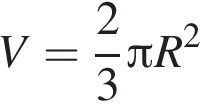

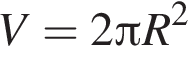
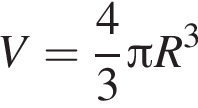
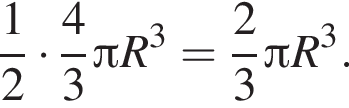
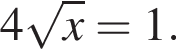
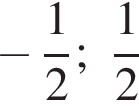
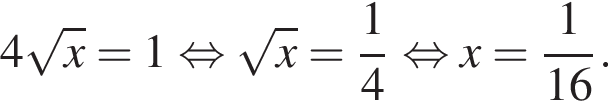
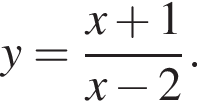

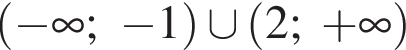

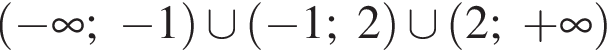
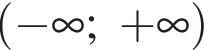

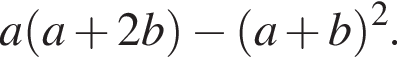
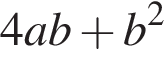
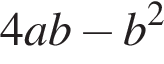
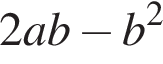
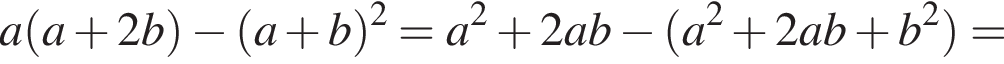
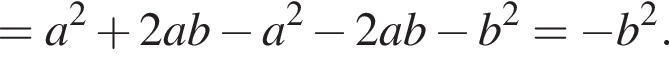
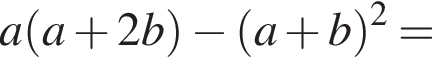
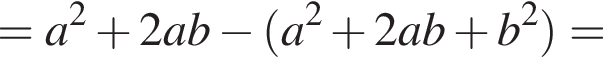
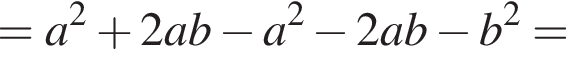
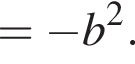

 как накрест лежащие. Значит,
как накрест лежащие. Значит, 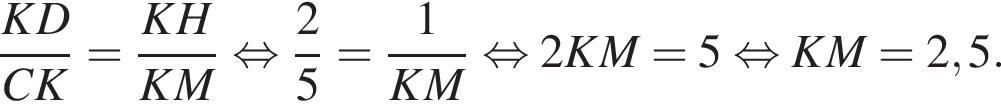
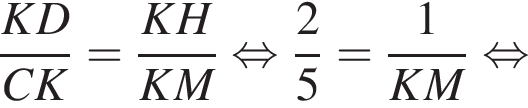


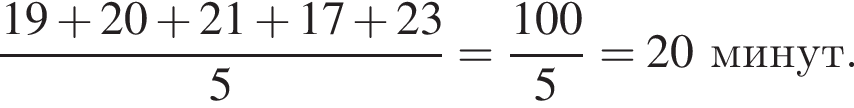
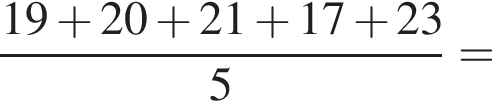
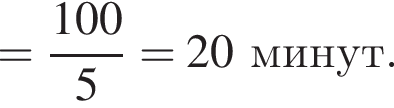
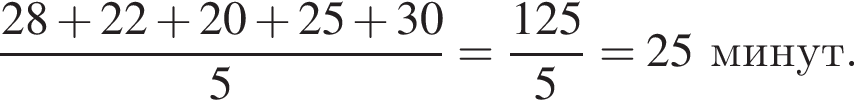
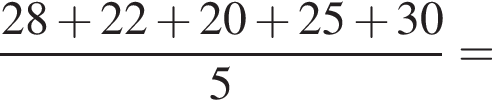
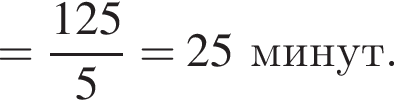
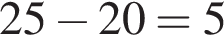 минут.
минут.

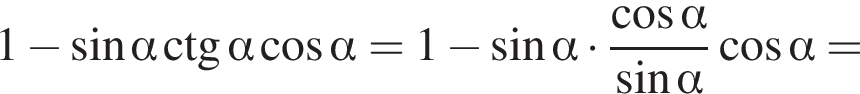
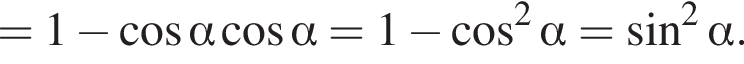
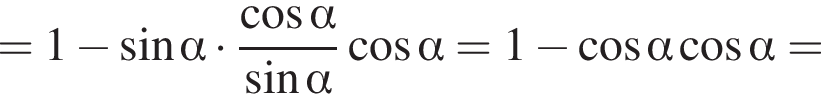
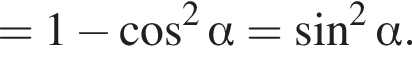
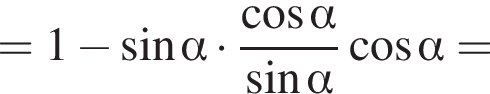

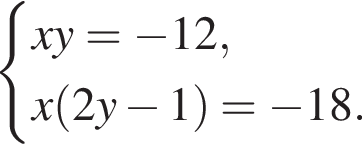
 и
и 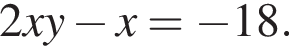 Вычитая из первого из этих уравнений второе, получим
Вычитая из первого из этих уравнений второе, получим 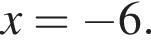
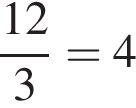 см
см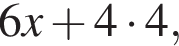 откуда
откуда 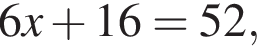

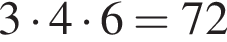 см2.
см2.
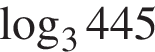
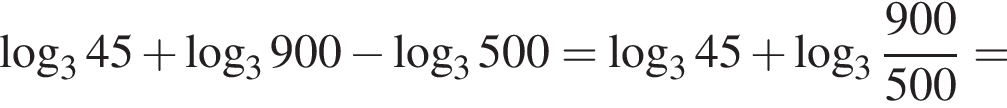
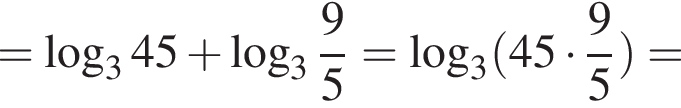
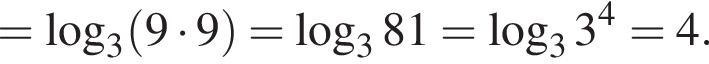

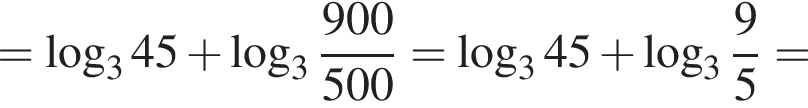
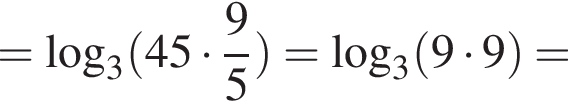
 яка визначена на множині дійсних чисел. Укажіть серед наведених точку, що належить цьому графіку.
яка визначена на множині дійсних чисел. Укажіть серед наведених точку, що належить цьому графіку.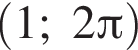

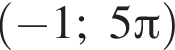


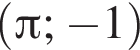 лежит на графике, имеем:
лежит на графике, имеем: 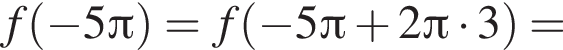

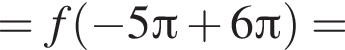

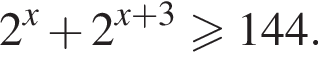
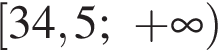

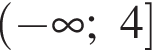
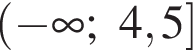
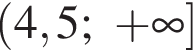
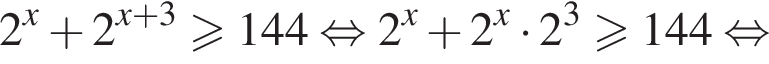
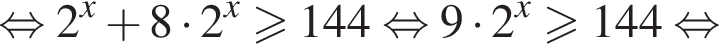
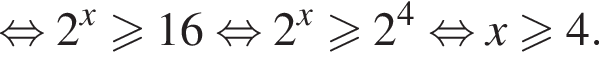
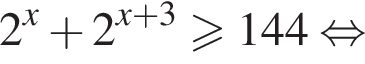
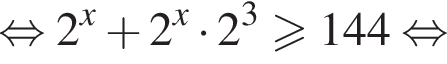
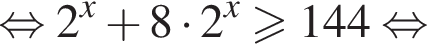
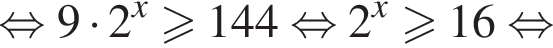
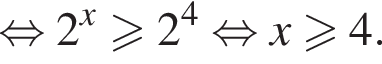
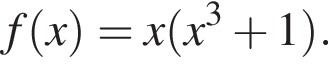
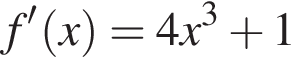
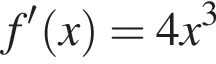
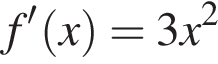
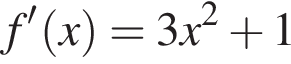
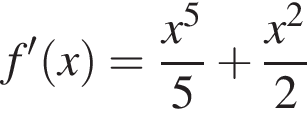
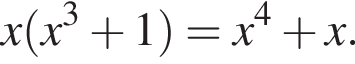 Найдем производную суммы двух функций:
Найдем производную суммы двух функций: 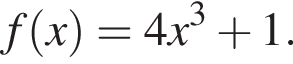
 м
м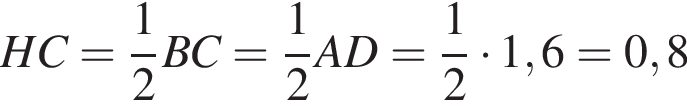 м
м

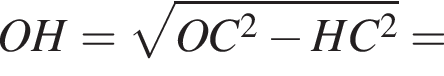
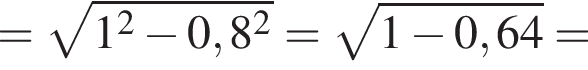
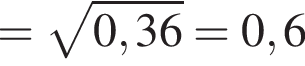
 м
м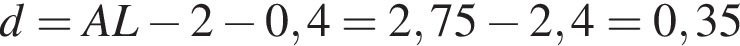 м.
м.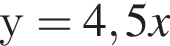
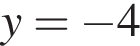
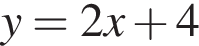
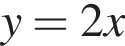
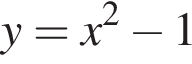
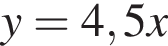 пересекается с графиком
пересекается с графиком  Тогда
Тогда 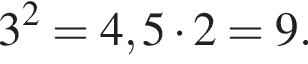 Таким образом, ответ — В.
Таким образом, ответ — В. 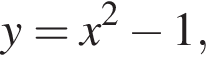 так как график
так как график 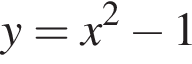 является параболой, ветви которой направлены вверх и вершина которой имеет координаты (0; −1), а график функции
является параболой, ветви которой направлены вверх и вершина которой имеет координаты (0; −1), а график функции 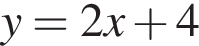 и
и 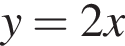 параллельны, так как они имеют одинаковый угловой коэффициент
параллельны, так как они имеют одинаковый угловой коэффициент 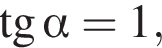 откуда найдем угол наклона прямой до положительного направления оси Ox:
откуда найдем угол наклона прямой до положительного направления оси Ox: 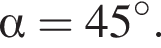 Таким образом, ответ — Д.
Таким образом, ответ — Д.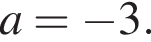
 Ответ — Б.
Ответ — Б. 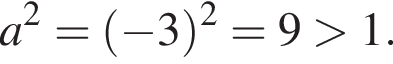 Ответ — A.
Ответ — A. 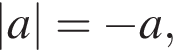 значит,
значит, 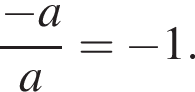 Ответ — Г.
Ответ — Г. 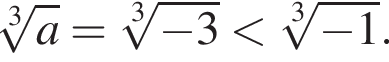 Ответ — Д.
Ответ — Д. 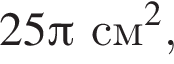 а його об’єм —
а його об’єм — 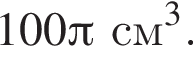 До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження. отсюда
отсюда  Тогда
Тогда 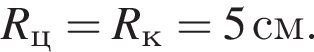 Итак, 3 — B.
Итак, 3 — B.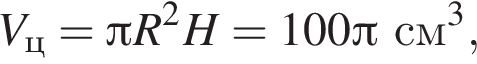
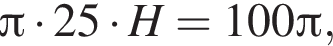 отсюда
отсюда 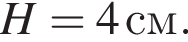 Высота цилиндра равна 4 см, получаем: 1 — А.
Высота цилиндра равна 4 см, получаем: 1 — А.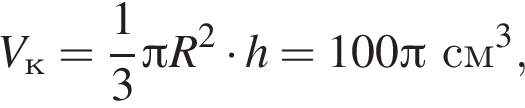
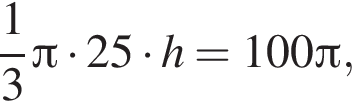 отсюда
отсюда 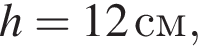 следовательно, 2 — Г.
следовательно, 2 — Г. 
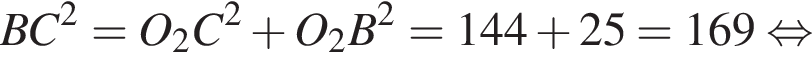

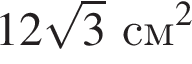
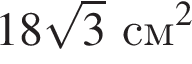
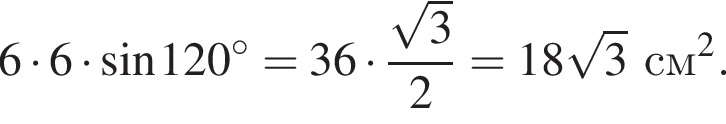
 см2
см2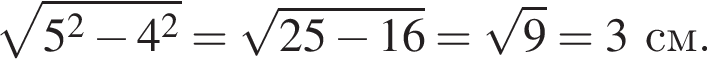
 см2
см2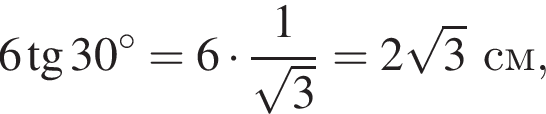
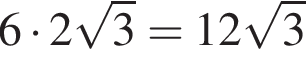 см2.
см2.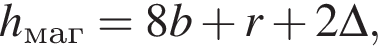 де
де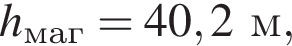 r = 10 м,
r = 10 м, 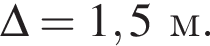
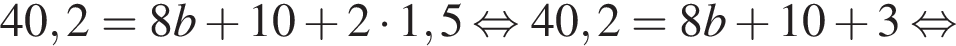

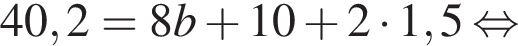

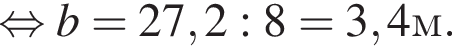
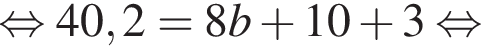

 метра, которые придется отобрать у разделительной полосы.
метра, которые придется отобрать у разделительной полосы. відстані від середини медіани BM до катетів АС і BC дорівнюють 5 см і 6 см відповідно.
відстані від середини медіани BM до катетів АС і BC дорівнюють 5 см і 6 см відповідно. м
м см
см см.
см.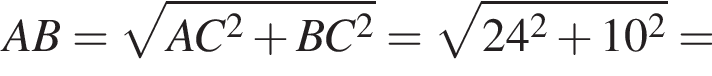

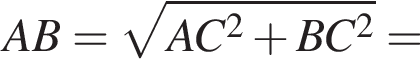
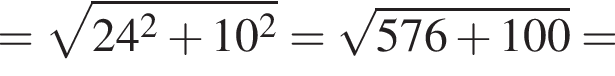
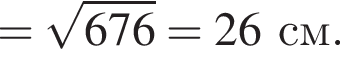
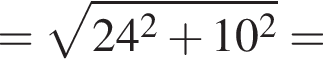
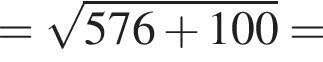
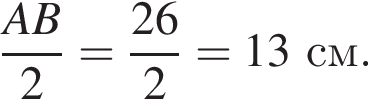
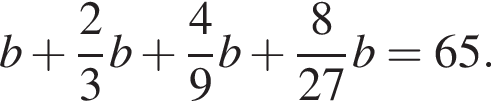
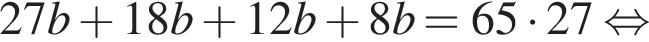
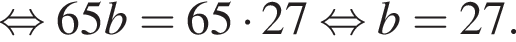
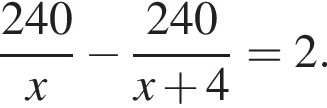
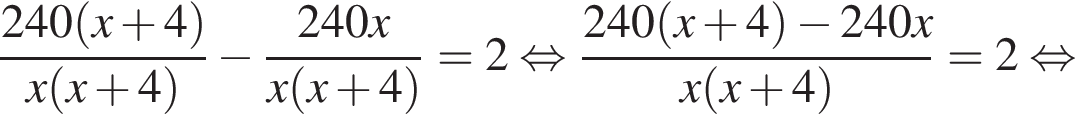
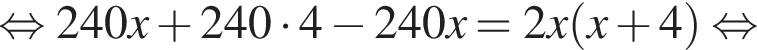


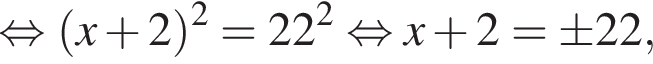
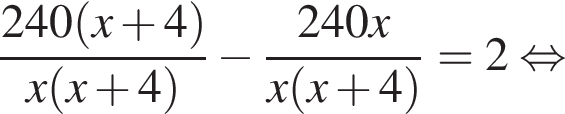
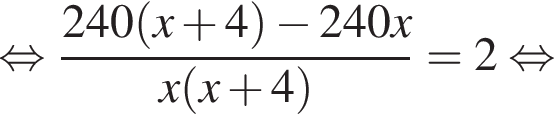
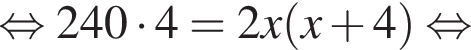
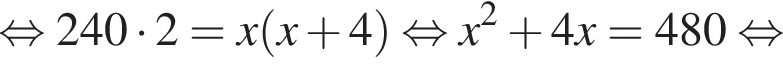
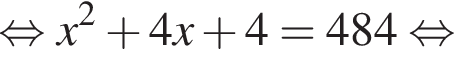

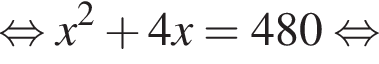
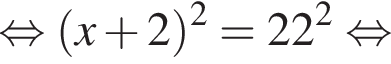
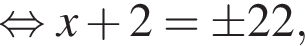
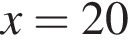 и
и 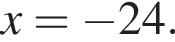 Второй случай невозможен. Итак,
Второй случай невозможен. Итак,  а срок по плану составлял
а срок по плану составлял 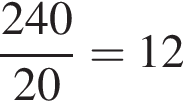 дней.
дней.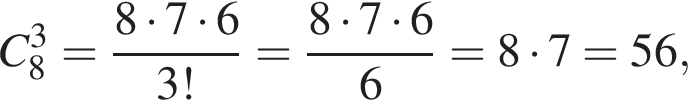
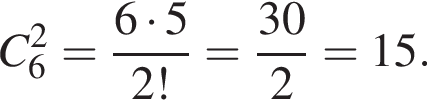
 способов.
способов.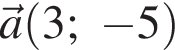 Визначте абсцису точки В, якщо А(−4; 1), а точка В лежить на прямій y = 3.
Визначте абсцису точки В, якщо А(−4; 1), а точка В лежить на прямій y = 3.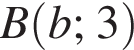 и
и 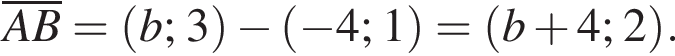 Вектора коллинеарны, если их координаты пропорциональны, поэтому
Вектора коллинеарны, если их координаты пропорциональны, поэтому 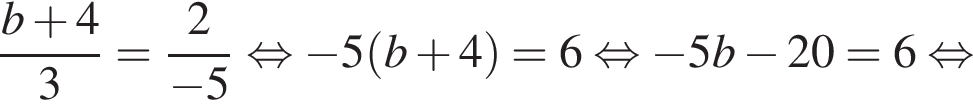
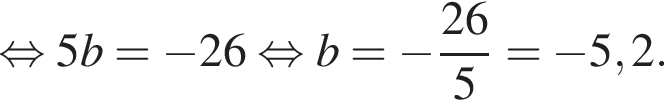
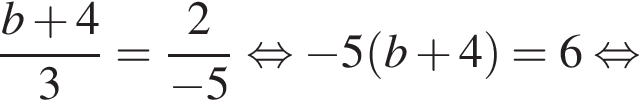
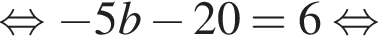
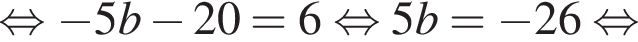
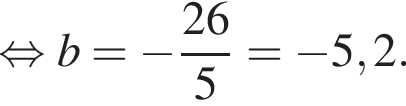
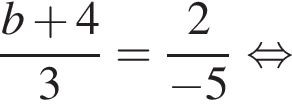
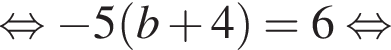
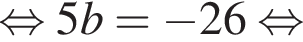
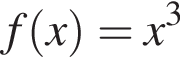 i
i 
 представлены на рисунке. Первый из них стандартный, а второй получается из графиков
представлены на рисунке. Первый из них стандартный, а второй получается из графиков  при
при 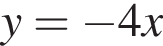 при
при 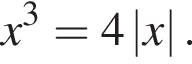 Ясно, что при
Ясно, что при 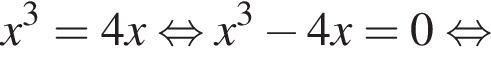
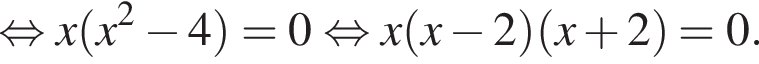
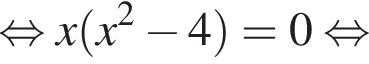
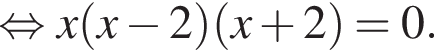
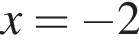 (последний корень не учитывается, поскольку
(последний корень не учитывается, поскольку 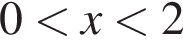 график
график 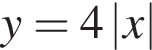 проходит выше графика
проходит выше графика 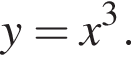 Значит, ограниченная ими площадь равна
Значит, ограниченная ими площадь равна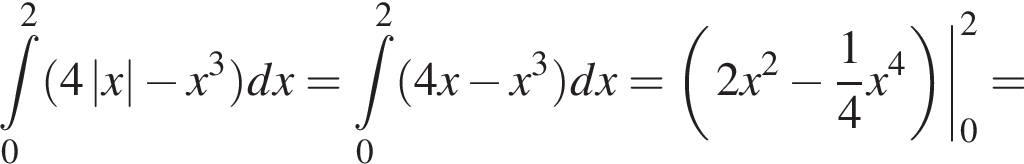
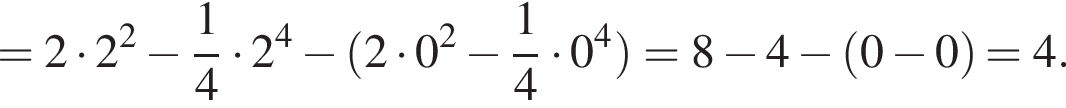
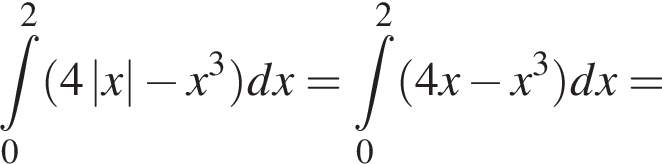
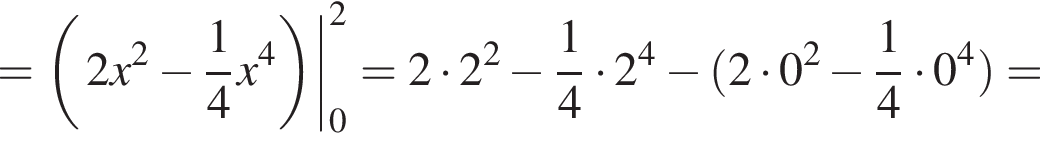

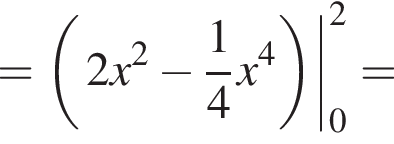
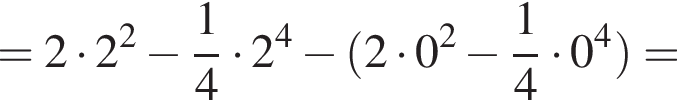
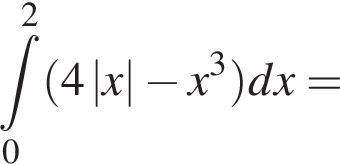
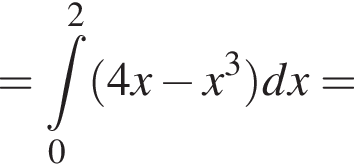
 поэтому сечение — трапеция. Найдем ее стороны. Заметим сразу, что
поэтому сечение — трапеция. Найдем ее стороны. Заметим сразу, что 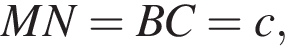 а
а 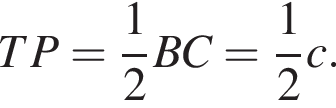 Проекцией SA на плоскость основания является OA, тогда по условию
Проекцией SA на плоскость основания является OA, тогда по условию 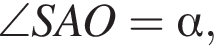 откуда
откуда 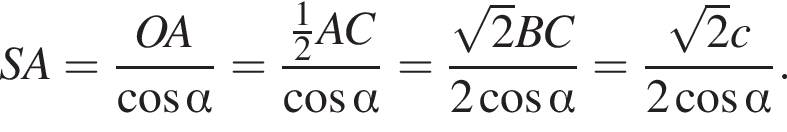
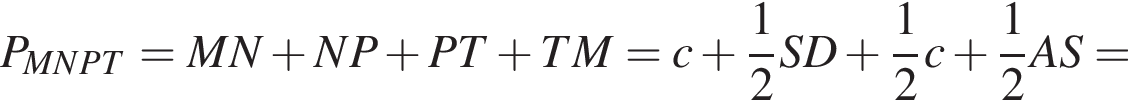
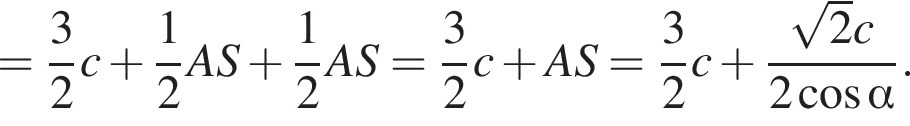
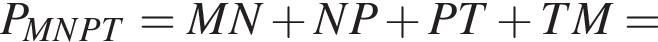
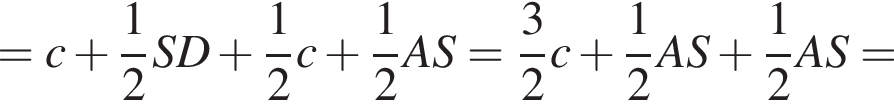
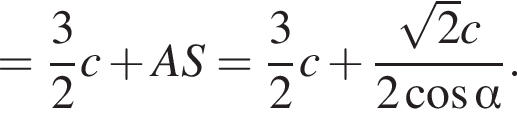
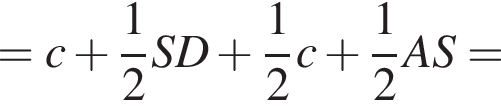
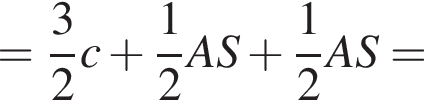


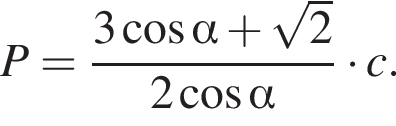
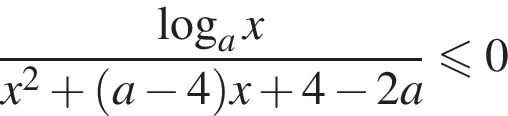 залежно вiд значень параметра a.
залежно вiд значень параметра a.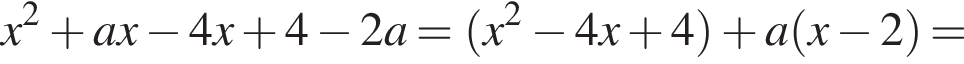
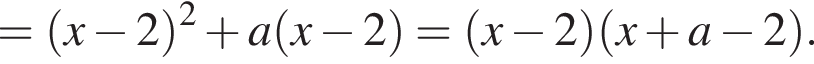
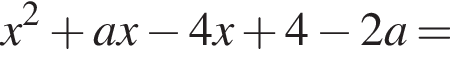
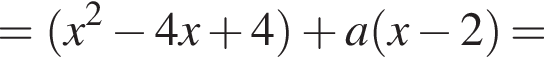
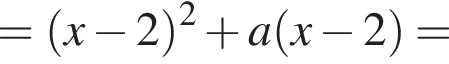
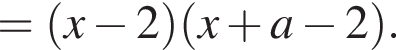
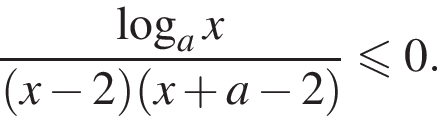
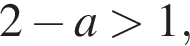 то числитель положителен при
то числитель положителен при  и положителен при
и положителен при 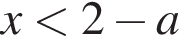 и при
и при 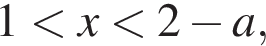 числитель отрицателен, знаменатель положителен, и при
числитель отрицателен, знаменатель положителен, и при 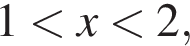 то
то  Числитель положителен при
Числитель положителен при 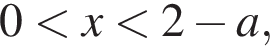 числитель отрицателен, знаменатель положителен, и при
числитель отрицателен, знаменатель положителен, и при 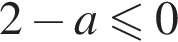 и рассматривать
и рассматривать  то
то 
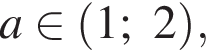 то
то 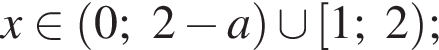
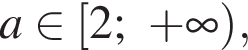 то
то