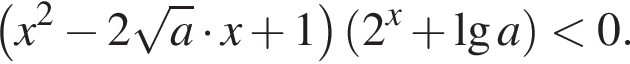Розташуйте у порядку спадання числа ![]()
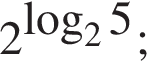
![]()
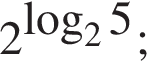
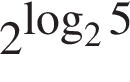
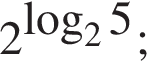
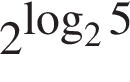
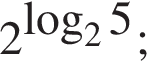
Розташуйте у порядку спадання числа ![]()
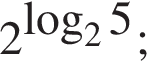
![]()
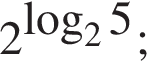
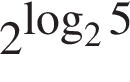
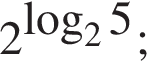
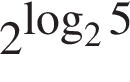
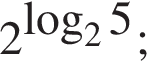
Банк сплачує своїм вкладникам 8% річних. Визначте, скільки грошей треба покласти на рахунок, шоб через рік отримати 60 грн. прибутку.
З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30?
Розв'яжіть нерівність 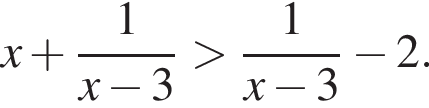
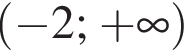


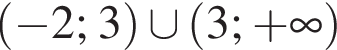
Знайдіть область визначення функції 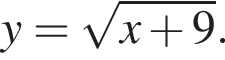


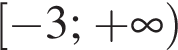
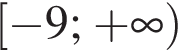
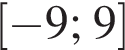
Будівельна компанія закупила для нового будинку металопластикові вікна та двері у відношенні 4 : 1. Укажіть число, яким може виражатися загальна кількість вікон та дверей в цьому будинку.
Обчисліть 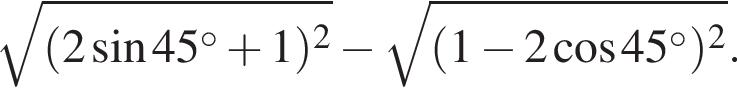
Розв яжіть ршняння 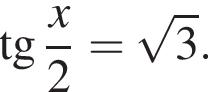
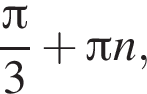
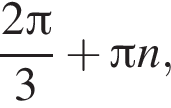
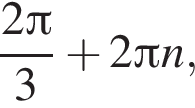
За видом графіка функції
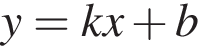 визначте знаки коефіцієнтів k i b. Оберіть правильне твердження.
визначте знаки коефіцієнтів k i b. Оберіть правильне твердження.
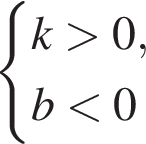
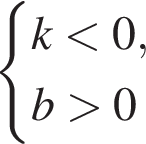
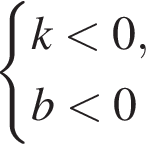
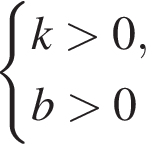
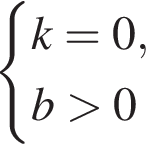
Укажіть парну функцію.
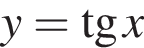
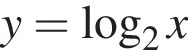
Обчисліть 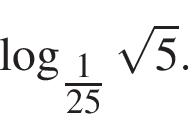
Розв'яжіть нерівність 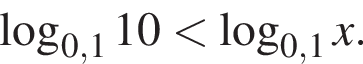
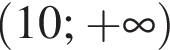
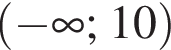
Розв'яжіть рівняння 
Укажіть, скільки дійсних коренів має рівняння 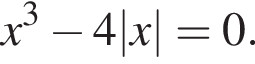
Знайдіть первісну функції  графік якої проходить через точку з координатами (1; 4).
графік якої проходить через точку з координатами (1; 4).
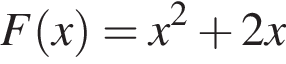
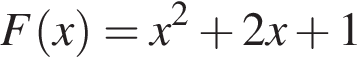
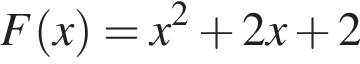
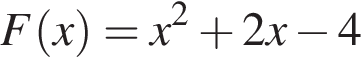
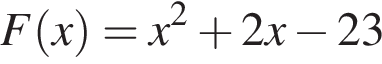
На рисунку зображений графік функції 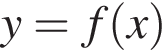 та дотичні до нього в точках x1 та x2. Користуючись геометричним змістом похідної, знайдіть
та дотичні до нього в точках x1 та x2. Користуючись геометричним змістом похідної, знайдіть 
Градусна міра зовнішнього кута A рівнобедреного трикутника ABC
 становить 125°. Знайдіть градусну міру внутрішнього кута B.
становить 125°. Знайдіть градусну міру внутрішнього кута B.
Точка М — середина сторони квадрата ABCD. Площа зафарбованої частини 7 см2, дорівнює 7 см. Знайдіть площу всього квадрата.
Знайдіть координати точки M, відносно якої симетричні точки E (−3; 8; 7) і F (−9; 6; 1).
Знайдіть об:єм тіла, утвореного обертанням круга навколо свого діаметра, довжина якого дорівнює a см.
Обчисліть 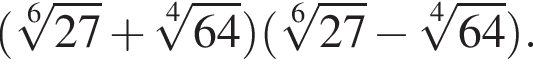
Знайдіть суму перших дванадцяти непарних натуральних чисел.
Укажіть найменше ціле число, яке є розв'язком нерівності
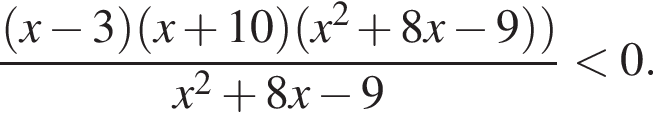
На перегоні, довжина якого дорівнює 240 км, поїзд рухався зі швидкістю на 10 км/год менше, ніж мала бути за розкладом, і запізнився на 48 хв. З якою швидкістю мав рухатися поїзд за розкладом? Відповідь в км/год.
Обчисліть 
Розв’яжіть рівняння 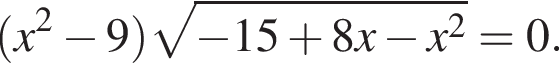 У відповідь запишіть сухгу коренів.
У відповідь запишіть сухгу коренів.
Розв’яжіть систему рівнянь
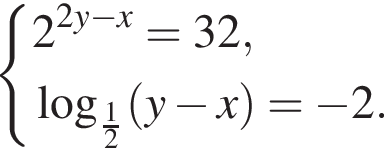
Запишіть у відповідь добуток ![]() якщо пара
якщо пара 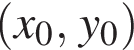 є розв'язком вказаної системи різнянь.
є розв'язком вказаної системи різнянь.
Середній вік одинадцяти футболістів команди становить 22 роки, Під час гри одного з футболістів було вилучено з поля, після чого середній вік гравців, що залишилися, став 21 рік. Скільки років футболісту, який залишив поле?
Обчисліть 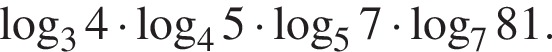
Знайдіть найбільше ціле значення параметра a, при якому система рівнянь
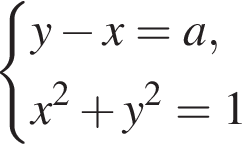
мас два розв'язки.
Знайдіть найбільше значення функції 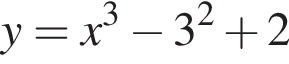 на проміжку [−1; 1].
на проміжку [−1; 1].
Знайдіть найменше ціле значення параметра a, при якому рівняння

має корені.
Сторона рівностороннього трикутника ABC дорівнює 5 см. Знайдіть скалярний добуток 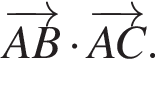
Для опалювальної системи будинку необхідні радіатори із розрахунку: три одиниці на 50 м3. Яку кількість одиниць радіатор їв треба замовити, якщо новий будинок має форму прямокутного паралелепіпеда розміру 15 м×18 м×25 м?
Апофема правильної чотирикутної пір аміли дорівнює ![]() см
см
У правильній чотирикутній піраміді SABCD (S — вершина) бічне ребро вдвічі більше сторони основи. Знайдіть кут між медіаною трикутника SDC, проведеною з вершини D, та середньою лінією трикутника ASC, шо паралельна основі піраміди.
Побудуйте графік функціі 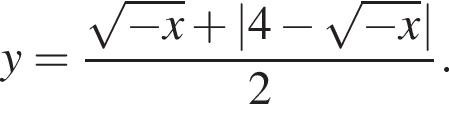
Розв'яжіть нерівність