Тип 20 № 805 
Справедливість тверджень стереометрії. Багатогранники
i
 У прямокутній системі координат у просторі зображено прямокутний паралелепіпед ABCDA1B1C1D1, вершина B якого збігається з початком координат, а вершини A, C i B належать осям x, у і z відповідно (див. рисунок). Вершина D1 має координати (4; 8; 12).
У прямокутній системі координат у просторі зображено прямокутний паралелепіпед ABCDA1B1C1D1, вершина B якого збігається з початком координат, а вершини A, C i B належать осям x, у і z відповідно (див. рисунок). Вершина D1 має координати (4; 8; 12).
До кожного початку речення (1—4) доберіть його закінчення (А—Д) так, щоб утворилося правильне твердження.
Початок речення
1. Серединою відрізка BC є точкає
2. Вектор  має координати
має координати
3. Точка, що належить відрізку DD1 і віддалена від точки D на 4 одиниці, має координати
4. Точка С1 має координати
Закінчення речення
А (0; 8; 12)
Б (4; 0; 0)
В (4; 8; 8)
Г (0; 4; 0)
Д (4; 8; 4)
Решение. Вершина B прямоугольного параллелепипеда ABCDA1B1C1D1 совпадает с точкой начала координат. Ребра BA, BC, BB1 параллелепипеда принадлежат на осях x, y, z соответственно, поэтому плоскости, содержащие грани параллелепипеда, перпендикулярны соответствующим осям координат. Вершина D1 имеет координаты (4; 8; 12), по ним можно определить координаты остальных вершин параллелепипеда. Точка A является точкой пересечения плоскости, которая проходит через точку D1 перпендикулярно оси x, поэтому абсцисса точки A совпадает с абсциссой точки D1, они равны 4. Координаты y и z точки A равны 0, так как точка A лежит на оси x. Поэтому A (4; 0; 0). Аналогично определим координаты точки C: (0; 8; 0).
1. Точка M — середина отрезка BC. Ее координаты можно определить по формуле:
Координаты середины отрезка BC найдем по формуле:
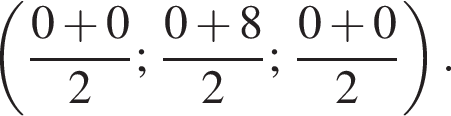
Итак, 1 — Г.
2. Для того, чтобы найти координаты вектора 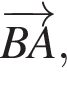 вычтем из координат конечной точки координаты точки начала вектора:
вычтем из координат конечной точки координаты точки начала вектора:
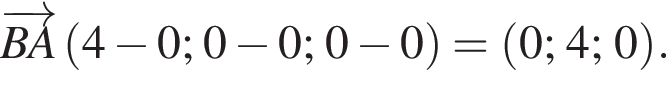
Итак, 2 — Б.
Отметим, что если точка, являющаяся началом вектора, совпадает с точкой начала координат, то координаты вектора совпадают с координатами его конечной точки.
3. Ребро DD1 параллельно оси z. Значит, координаты каждой точки, принадлежащей данному ребру, имеют вид (4; 8; z), причем 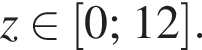 Точка, удаленная от вершины D на 4 единицы и лежащая на ребре DD1, имеет координаты (4; 8; 4). Таким образом, 3 — Д.
Точка, удаленная от вершины D на 4 единицы и лежащая на ребре DD1, имеет координаты (4; 8; 4). Таким образом, 3 — Д.
4. Координатная плоскость yz задается уравнением x = 0. Рассматривая точку C1 как проекцию точки D1 на плоскость yz, получим ее координаты: (0; 8; 12). Следовательно, 4 — А.
Ответ: 1 — Г, 2 — Б, 3 — Д, 4 — А.
Ответ: Г&Б&Д&А
У прямокутній системі координат у просторі зображено прямокутний паралелепіпед ABCDA1B1C1D1, вершина B якого збігається з початком координат, а вершини A, C i B належать осям x, у і z відповідно (див. рисунок). Вершина D1 має координати (4; 8; 12).
![]() має координати
має координати
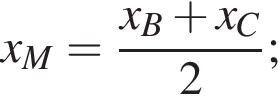
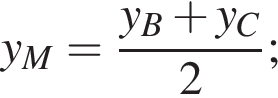
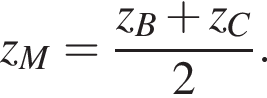
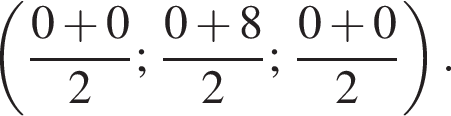
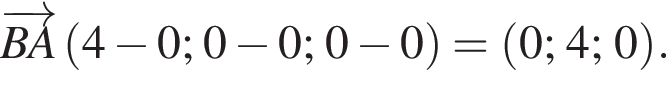
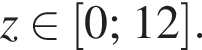 Точка, удаленная от вершины D на 4 единицы и лежащая на ребре DD1, имеет координаты (4; 8; 4). Таким образом, 3 — Д.
Точка, удаленная от вершины D на 4 единицы и лежащая на ребре DD1, имеет координаты (4; 8; 4). Таким образом, 3 — Д.