Задано рівняння
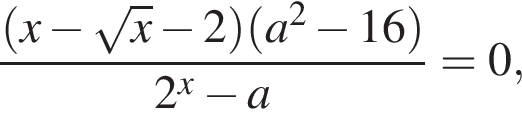
де x — змінна, a — стала.
1. Розв’яжіть рівняння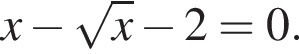 
2. Розв’яжіть задане рівняння залежно від значень а.
Решение. Решим уравнение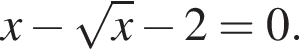 
Преобразуя его, получим
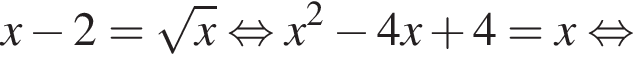
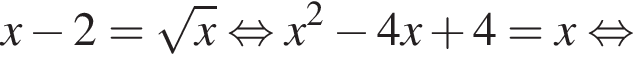
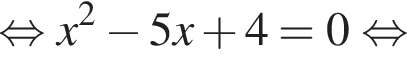
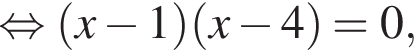
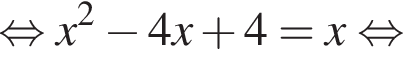
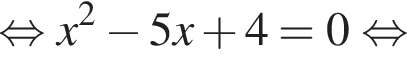
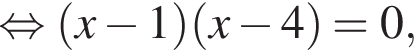
тогда 
или 
(посторонний корень, появился при возведении в квадрат). По второму пункту сразу заметим, что если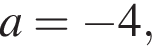 
то числитель равен нулю всегда, когда определен, а знаменатель никогда не равен нулю. Значит, 
Аналогично, при 
числитель равен нулю всегда, когда определен, а знаменатель равен нулю при 
Значит, 
При прочих a можно разделить уравнение на 
и получить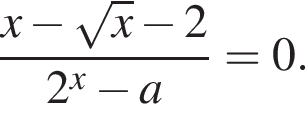 
Числитель равен нулю только при и оно является корнем при всех a, кроме тех, для которых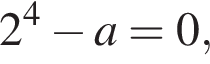 
то есть кроме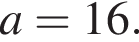 
Ответ:
1. x = 4;
2. якщо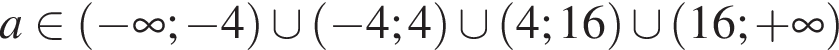 
, то 
— a = −4, то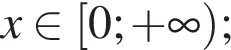 
— якщо a = 4, то 
— якщо a = 16, то рівняння коренів не має.
1. x = 4;
2. якщ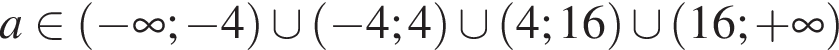о , то
— a = −4, то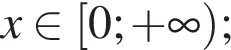
— якщо a = 4, то
— якщо a = 16, то рівняння коренів не має.
1. x = 4;
2. якщ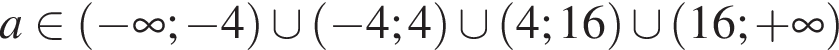о , то
— a = −4, то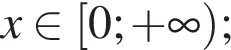
— якщо a = 4, то
— якщо a = 16, то рівняння коренів не має.