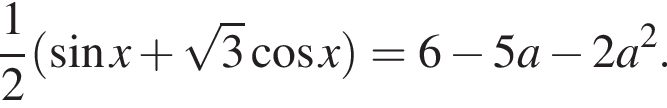Розв'яжіть рівняння ![]()

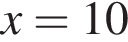



Розв'яжіть рівняння ![]()

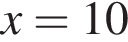



Учитель роздав учням певного класу 72 зошити. Кожен учень отримав однакову кількість зошитів. Якому з поданих нижче чисел може дорівнювати кількість учнів у цьому класі?<
Спростіть вираз 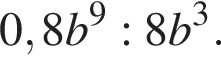
Укажіть лінійну функцію, графік якої паралельний вісі абсцис і проходить через точку A(−2; 3).
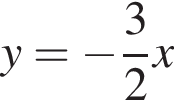

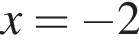
Доберіть таке закінчення речення, щоб утворилося правильне твердження: «Сума квадратів катетів прямокутного трикутника дорівнює...».
Обчисліть 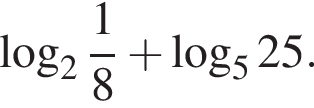
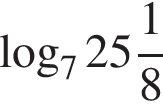
На рисунку зображено куб ABCDA1B1C1D1. Укажіть серед поданих нижче пряму, що утворюе з CD1 пару мимобіжних прямих.
Журнал коштував 25 грн. Через два місяці цей самий журнал став коштувати 21 грн. На скільки відсотків знизилася ціна журналу?
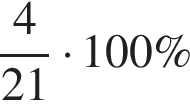
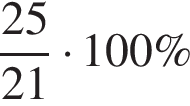
На одиничному колі зображено точку
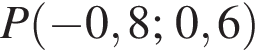 і кут α (див. рисунок). Визначте
і кут α (див. рисунок). Визначте ![]()
Знайдіть градусну міру внутрішнього кута правильного десятикутника.
Спростіть вираз  якщо
якщо ![]()
Об’єм кулі дорівнює 36π см3. Знайдіть її діаметр.
Визначте знаменник геометричної прогресії (bn), якщо 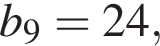
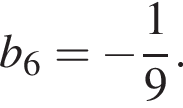
Розв'яжіть нерівність 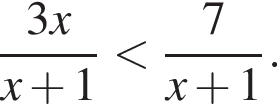
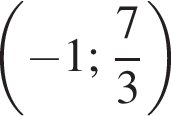
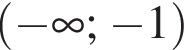
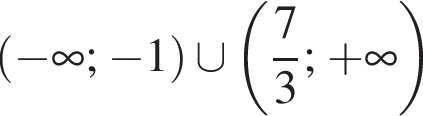
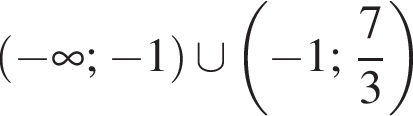
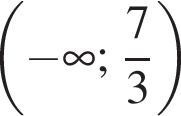
Обчисліть площу чотирикутника ABCD (див. рисунок), сторони АВ і CD якого паралельні вісі Oy.
Якому з наведених нижче проміжків належить корінь рівняння 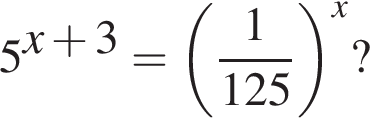
На рисунку зображено коло з центром у точці O і рівносторонній трикутник AOB, що перетинає коло в точках M і N. Точка D належить колу. Знайдіть градусну міру кута MDN.
Функція 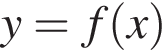 є спадною на проміжку
є спадною на проміжку 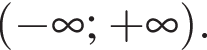 Укажіть правильну нерівність.
Укажіть правильну нерівність.

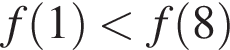



У прямокутник ABCD вписано три круги одного й того самого радіуса (див. рисунок). Визначте довжину сторони BC, якщо загальна площа кругів дорівнює 3π.
О шостій годині ранку визначено температуру на десяти метеостанціях. Отримані дані відображено в таблиці.
| Температура (у градусах) | 1 | 3 | 4 | x |
| Kiльxiсть метеостанцiй | 2 | 3 | 4 | 1 |
Визначте х, якщо середнє арифметичне всіх цих даних дорівнює 3,5°.
У трикутнику ABC: 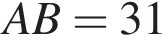 см,
см, см,
см,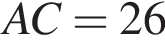 см.
см. см.
см.
На рисунку зображено розгортку циліндра. Знайдіть його об'єм.
Розв'яжіть нерівність 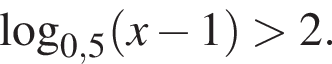

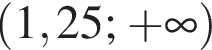
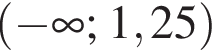
Функція  є первісною функції f(x). Знайдіть функцію f(x).
є первісною функції f(x). Знайдіть функцію f(x).
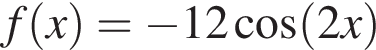
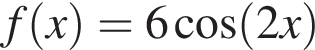
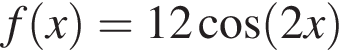


Діагональним перерізом правильної чотирикутної призми є прямокутник, площа якого дорівнюе 40 см2. Периметр основи призми дорівнюе ![]() см.
см.
Установіть відповідність між функціями (1−4) та ескізами їхніх графіків (А−Д).
1. 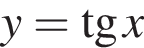
2. 
3. 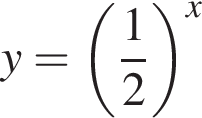
4. ![]()
На рисунку зображено вектори
![]()
![]()
![]()
![]() у прямокутній системі координат. Установіть відповідність між парою векторів (1−4) і твердженням (А−Д), що є правильним для цієї пари.
у прямокутній системі координат. Установіть відповідність між парою векторів (1−4) і твердженням (А−Д), що є правильним для цієї пари.
1. ![]() i
i ![]()
2. ![]() i
i ![]()
3. ![]() i
i ![]()
4. ![]() i
i ![]()
А вектори перпендикулярні
Б вектори колінеарні, але не рівні
В скалярний добуток векторів більший за 0
Г вектори рівні
Д кут між векторами тупий
Установіть відповідність між виразами (1−4) та їхніми значеннями, якщо  (А−Д).
(А−Д).
1. ![]()
2. 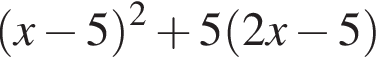
3. 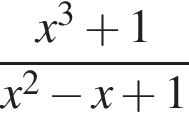
4. 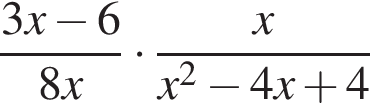
А −2,5
Б −0,25
В 0,25
Г 1,5
Д 2,5
Обчисліть значення виразу
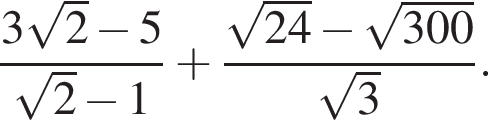
Матеріальна точка рухається за законом 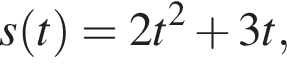 де s вимірюється в метрах, a t у секундах. Знайдіть значення t (у секундах), при якому миттєва швидкість матеріальної точки дорівнює 76 м/c.
де s вимірюється в метрах, a t у секундах. Знайдіть значення t (у секундах), при якому миттєва швидкість матеріальної точки дорівнює 76 м/c.
У відділі праццює певна кількість чоловіків і жінок. Для анкетування навмання вибрали одного із співробітників. Імовірність того, що це чоловік, дорівнює ![]() Зайдіть відношення кількості жінок до кількості чоловіків, які працюють у цьому відділі.
Зайдіть відношення кількості жінок до кількості чоловіків, які працюють у цьому відділі.
Двоє робітників, працюючи разом, можуть скосити траву на ділянці за 2 години 6 хвилин. Скільки часу (у годинах) витратить на скошування трави на цій ділянці другий робітник, працюючи самостійно, якщо йому потрібно на виконання цього завдання на 4 години більше, ніж першому робітникові?
У чотирикутну піраміду, в основї якої лежить рівнобічна трапеція з бічною стороною 13 см і основами ![]() і 8 см, вписано конус. Знайдіть площу бічної поверхні конуса Sбiчне (у см2) якщо всі бічні грані піраміди нахилені до площини основи під кутом 60°. У відповіді запишіть значення
і 8 см, вписано конус. Знайдіть площу бічної поверхні конуса Sбiчне (у см2) якщо всі бічні грані піраміди нахилені до площини основи під кутом 60°. У відповіді запишіть значення 
На рисунку зображено графік функціі 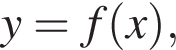 що визначена на проміжку
що визначена на проміжку  і має лише три нулі.
і має лише три нулі.
Розв'яжіть систему
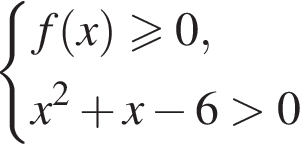
У відповіді запишіть суму всіх цілих розв'язків системи.
Знайдіть найменше значення a, при якому мас розв'язки рівняння