1.
i
У саду в окремі ящики зібрали груші та яблука. Кількість ящиків з яблуками відноситься до кількості ящиків з грушами,
А) 37
Б) 73
В) 75
Г) 80
Д) 84
СКЛАДУ ЗНО — математика
Вариант № 6
ЗНО 2010 року з математики (1 варіант) — пробний тест
2.
i
Точка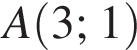 
належить колу з центром у точці 
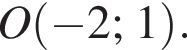Знайдіть радіус ццого кола.
3.
i
Поле, площа якого дорівнюе 60 га, засіяли горохом і соєю. Горохом засіяли 
площі поля. Скільки всього гектарів поля засіяли соєю?
А) 10
Б) 15
В) 20
Г) 24
Д) 45
4.
i
На одному з наведених рисунків зображено ескіз графіка функції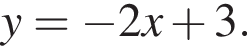 
Укажіть цей рисунок.
А) А
Б) Б
В) В
Г) Г
Д) Д
5.
i
Знайдіть довжину діагоналі прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см, 4 см.
А) 
см
смБ) 9 см
В) 
см
смГ) 5 см
Д) 
см
см6.
i
Якому з наведених проміжків належить корінь рівняння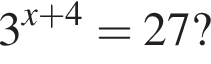 
А) [−4; −2)
Б) [−2; 0)
В) [0; 2)
Г) [2; 4)
Д) [4; 6)
7.
i
Діагоналі трапеції ABCD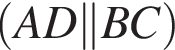 
перетинаються в точці O. Знайдіть довжину основи BC трапеції, якщо 
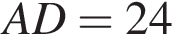см,
см,
см.
А) 6 см
Б) 9 см
В) 12 см
Г) 16 см
Д) 18 см
8.
i
Яке з наведених чисел е раціональним числом?
А) 
Б) 
В) π
Г) 
Д) 
9.
i
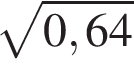
Знайдіть найбільший від’ємний член арифметичної прогресії 2,9; 2,2; 1,5; ...
А) −0,1
Б) −0,3
В) −0,6
Г) −0,8
Д) −1,3
10.
i
Бічна сторона рівнобедреного трикутника дорівнює 10 см, а висота, опущена на неї, — 8 см. Знайдіть довжину основи трикутника.
А) 6 см
Б) 
см
смВ) 12 см
Г) 
см
смД) 16 см
11.
i
Упродовж чверті учень отримав 12 оцінок з алгебри. Інформацію про отримані оцінки та їхню кількість відображено в таблиці.
| Оцінка | 5 | 6 | 7 | 8 | 10 |
| Кількість оцінок | 2 | 1 | 3 | 5 | 1 |
Знайдіть середнє арифметичне всіх оцінок, отриманих учнем упродовж чверті.
А) 7
Б) 7,2
В) 7,25
Г) 8
Д) 8,1
12.
i
Облисліть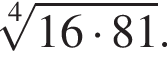 
А) 6
Б) 12
В) 18
Г) 36
Д) 72
13.
i
При яких значеннях m і n вектори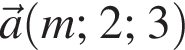 
і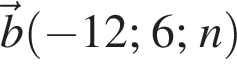 
колінеарні?
А) 
i 
i Б) 
i 
i В) i
i Г) 
i
i Д) i
i 14.
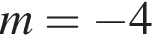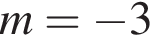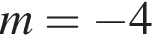i
Розташуйте в порядку зростання числа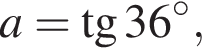 
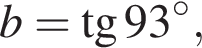
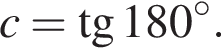
А) b; c; a
Б) c; b; a
В) a; b; c
Г) c; a; b
Д) b; a; c
15.
i
Периметр бічної грані правильної трикутної призми дорівнює 20 см. Знайдіть площу бічної поверхні призми, якщо сторона II основи дорівнюе 4 см.
А) 96 см2
Б) 80 см2
В) 72 см2
Г) 32 см2
Д) 24 см2
16.
i
Розв'яжіть нерівність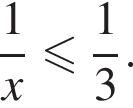 
17.
i
Подайте вираз 
у вигляді степеня з основою a.
А) 
Б) a−6
В) 
Г) a7
Д) 
18.
i
На полиці розміщено 16 книг, з яких 6 книг — історичні романи, а решта - детективи. Знайдіть імовірність того, що перша книга, навмання взята з полиці, буде детективом.
А) 
Б) 
В) 
Г) 
Д) 
19.
i
Точки А і В належать колу радіуса 10 см і ділять його на дві дуги, довжини яких відносяться як 3 : 2. Знайдіть довжину більшої дуги кола.
А) 20π см
Б) 12π см
В) 8π см
Г) 6π см
Д) 4π см
20.
i
Обчисліть площу зафарбованої фігури, зображеної на рисунку.
А) 
Б) 
В) 1
Г) 
Д) 
21.
i
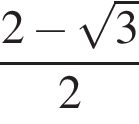
Які з наведених тверджень правильні?
І. Якщо коло має з площиною дві спільні точки, то всі точки кола належать цій площині.
II. Якщо три вершини паралелограма належать площині, то всі точки паралелограма належать цій площині.
III. Якщо круг і площина мають три спільні точки, то всі точки круга належать цій площині.
А) лише II
Б) лише III
В) лише I і II
Г) лише I і III
Д) лише II і III
22.
i
Розв’яжіть нерівність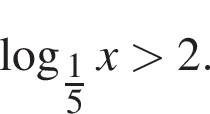 
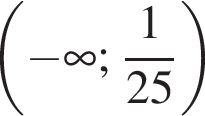
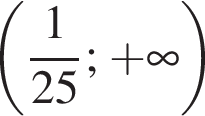
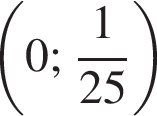
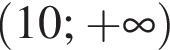
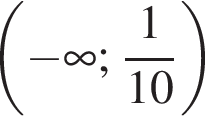
А) 
Б) 
В) 
Г) 
Д) 
23.
i
Об'єм циліндра дорівнює 48 см3. Знайдіть об’єм конуса, радіус основи якого дорівнює радіусу основи циліндра, а висота вдвічі менша за висоту ци.
А) 6 см3
Б) 8 см3
В) 16 см3
Г) 24 см3
Д) 36 см3
24.
i
У кіоску є 10 видів вітальних листівок з Новим роком. Скільки всього можна утворити різних наборів листівок, кожен із яких складається з трьох листівок різних видів?
А) 30
Б) 90
В) 120
Г) 240
Д) 720
25.
i
Прямі, що містять сторони правильного п'ятикутника ABCDF, перетинаються у точках K, L, M, N, P. Знайдіть градусну міру кута AKB.
А) 18°
Б) 26°
В) 30°
Г) 36°
Д) 60°
26.
i
Установіть відповідність між числовими виразами (1−4) та їхніми значеннями (А−Д).
1. 
2. 
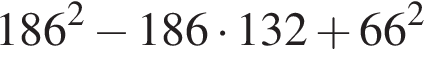
3. 
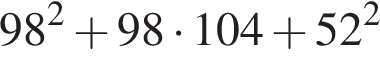
4. 
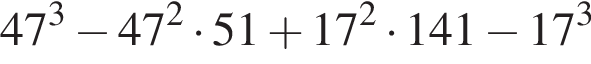
А 64 000
Б 27 000
В 24 000
Г 22 500
Д 14 400
А
Б
В
Г
Д
1
2
3
4
27.
i
Установіть відповідність між функціями, заданими формулами (1−4), та їхніми областями значень (А−Д).
1. 
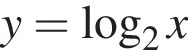
2. 
3. 
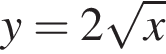
4. 
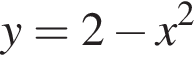
А 
Б 
В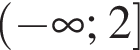 
Г 
Д 
А
Б
В
Г
Д
1
2
3
4
28.
i
На рисунках (1−4) зображено куб і три точки, що розміщені у вершинах куба або є серединами його ребер. Установіть відповідність між кожним рисунком (1−4) та назвою фігури (А−Д), яка є перерізом куба площиною, що проходить через три задані точки.
А трикутник
Б прямокутник
В трапеція
Г п'ятикутник
Д ромб
А
Б
В
Г
Д
1
2
3
4
29.
i
Знайдіть значення похідної функції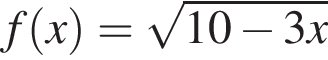 
у точці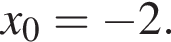 
30.
i
Маючи 4 кг огірків і 5 кг помідорів коштували 44 гривні. Після того як огірки подорожчали на 50%, а помідори подешевшали на 40%, за 4 кг огірків і 5 кг помідорів заплатили 39 гривень. Знайдіть початкову вартість x одного кілограма огірків і початкову вартість y одного кілограма помідорів. 
відповідь запишіть суму 
(y грн).
31.
i
Обчисліть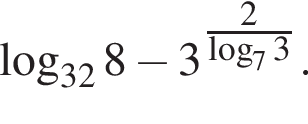 
32.
i
Функцію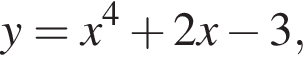 
визначену на множині всіх дійсних чисел, подайте у вигляді 
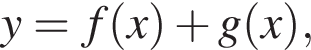де f(x) — парна функція, g(x) — непарна функція. У відповідь запишіть значення виразу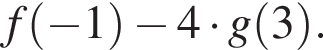 
33.
i
Розв'яжіть рівняння
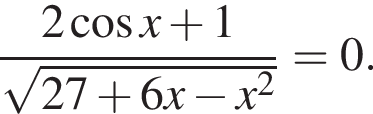
У відповідь запишіть кількість усіх його коренів. Якщо рівняння мае безліч коренів, то у відповідь запишіть число 100.
34.
i
Точки K і L — середини сторін AB і AD паралелограма ABCD (див. рисунок). Знайдіть площу п'ятикутника KBCDL (y см2), якщо площа паралелограма ABCD дорівнюе 24 см2.
35.
i
Знайдіть найбільше значення параметра a, при якому рівняння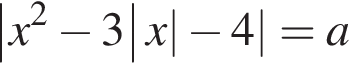 
має тільки чотири корені. Якщо такого значення a не існує, то у відповідь запишіть число 100.
36.
i
У правильну чотирикутну піраміду вписано сферу, площа якої дорівнюе 36π см2. Бічна грань піраміди нахилена до площини і основи під кутом 60°. Знайдіть об'єм пірамдии (у см3).