Спростіть вираз 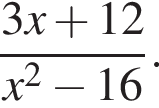
А) 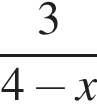
Б) 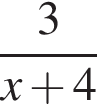
В) 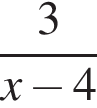
Г) 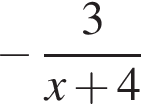
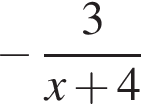
Д) 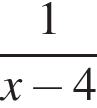
Решение. Завдання до 2015 року поки що не вирішені.
Ответ: 3
69
3
Спростіть вираз 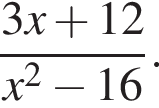
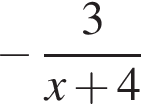
У трикутнику ABC:
 BD — бісектриса кута B (див. рисунок). Знайдіть градусну міру кута BCA, якщо
BD — бісектриса кута B (див. рисунок). Знайдіть градусну міру кута BCA, якщо 
Обчисліть 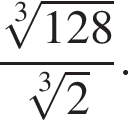
Яка з поданих нижче послідовностей є арифметичною прогресією? −9; −2; 0; 1
У Оксани є певна кількість горіхів. Коли вона розклала їх у купки по 5 горіхів, то два горіхи залишилися, а коли розклала їх по 3, то зайвих горіхів не виявилося. Яка кількість горіхів із запропонованих варіантів МОГЛА БУТИ в Оксани?
Розв’яжіть нерівність 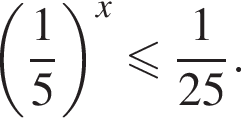
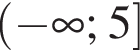


У сонячний день довжина тіні від дерева становить 16 м. У той самий час тінь від хлопчика, який має зріст 1,5 м, дорівнюе 2 м (див. рисунок). Визначте висоту дерева.
За переказ грошей клієнт повинен сплатити банку винагороду в розмірі 2% від суми переказу. Скільки всього грошей (у гривнях) йому потрібно сплатити в касу банку, якщо сума переказу становить 30 000 грн.
Якщо 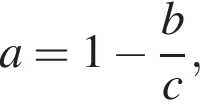 то b?
то b?
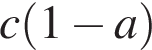
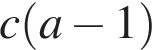
Укажіть правильну нерівність.
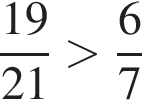
Укажіть рисунок, на якому зображено графік парної функції.
Знайдіть вектор 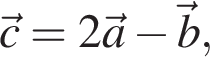 якщо
якщо  та
та 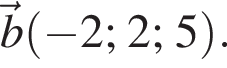
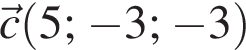
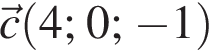
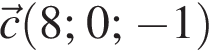
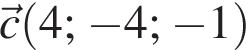
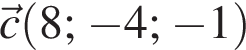
У туриста є 10 однакових за розмірами консервних банок, серед яких 4 банки — з тушкованим м’ясом, 6 банок — з рибою. Під час зливи етикетки відклеїлися. Турист навмання взяв одну банку. Яка ймовірність того, ідо вона буде з рибою?
Знайдіть похідну функції 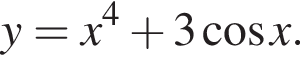
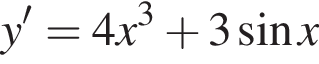
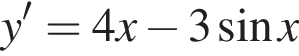
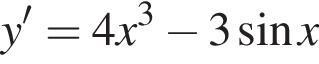
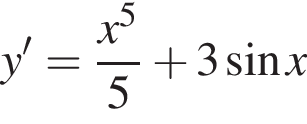
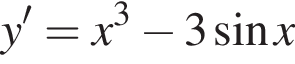
Укажіть УСІ ПРАВИЛЬНІ твердження.
I. Через точку А, що не належить площині а, можна провести лише одну пряму, паралельну площині а.
II. Через точку А, що не належить площині а, можна провести лише одну площину, паралельну площині а.
III. Через точку А, що не належить площині а, можна провести лише одну пряму, перпендикулярну до площини а.
IV. Через точку А, що не належить площині а, можна провести лише одну площину, перпендикулярну до площини а.
Графік функції
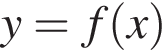 проходить через точку М (1; 1) (див. рисунок). При якому значенні а графік функції
проходить через точку М (1; 1) (див. рисунок). При якому значенні а графік функції 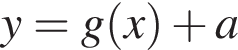 проходить через точку N (1; 3)?
проходить через точку N (1; 3)?
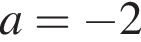
Розв’яжіть рівняння 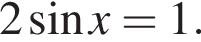
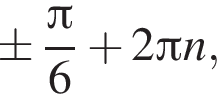
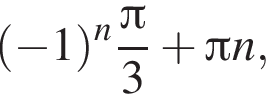
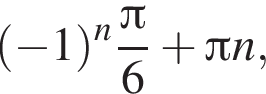
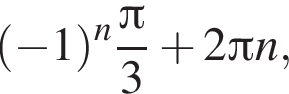
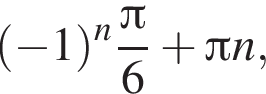
До складу української Прем’єр-ліги з футболу входять 16 команд. Упродовж сезону кожні дві команди грають між собою 2 матчі. Скільки всього матчів буде зіграно за сезон?
Гострий кут паралелограма дорівнює 60°, а його сторони — 3 см и 4 см. Обчисліть довжину меншої діагоналі паралелограма.
Свинцеву кулю радіуса 5 см переплавили в кульки однакового розміру, радіус кожної з яких — 1 см. Скільки таких кульок одержали? Втратами свинцю під час переплавлення знехтуйте.
Обчисліть 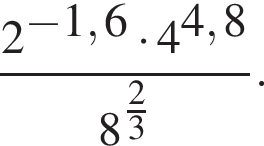
У трапеції ABCD:

 см
см см
см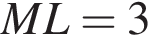 см.
см.
Обчисліть ![]() якщо
якщо  i
i 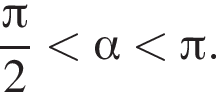
Об'єм куба ABCDA1B1C1D1 дорівнює 216 см3 (див. рисунок). Обчисліть об'єм піраміди D1ACD (у см3).
Розв'яжіть рівняння
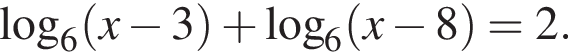
Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму.
У фермерському господарстві «Надія» кожен рік озимою пшеницею засівають 600 га полів. Середня врожайність цієї культури в 2007 році становила 24 центнери з одного гектара. Завдяки сприятливим погодним умовам у 2008 році озимої пшениці було зібрано на 19 200 центнерів більше, ніж у 2007. Обчисліть середню врожайність озимої пшениці, вирощеної у господарстві «Надія» в 2008 році (у ц/га). Середня врожайність сільськогосподарської культури — це відношення маси зібраного врожаю цієї культури до запальної площі полів, на яких вона була вирощена.
Знайдіть КІЛЫКІСТВ усіх цілих розв'язків нерівності
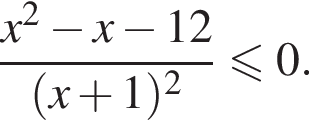
Якщо нерівність має безліч цілих розв'язків, то у відповідь запишіть число 100.
Кімната має форму прямокутного паралелепіпеда (ширина кімнати — 4 м, довжина — 5 м, висота — 2,5 м). Площа стін кімнати дорівнює 0,8 площі бічної поверхні цього паралелепіпеда. Скільки фарби (у кг) потрібно для того, щоб повністю пофарбувати СТІНИ і СТЕЛЮ цієї кімнати, якщо на 1 м2 витрачається 0,25 кг фарби?
Розв'яжіть систему рівнянь
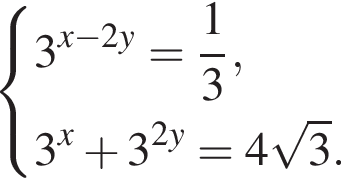
Для одержаного розв'язку (x0; у0) системи обчисліть ДОБУТОК ![]()
Знайдіть найбільше значення функції
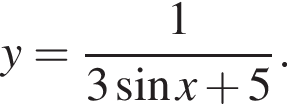
Якщо функція не має найбільшого значення, то у відповідь запишіть число 100.