Розв'яжіть нерівність 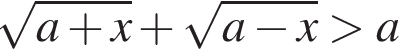 при всіх значеннях параметра a.
при всіх значеннях параметра a.
Решение. Сразу отметим, что неравенство определено при условиях 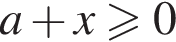 и
и 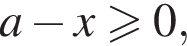 откуда
откуда 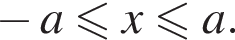 В частности
В частности 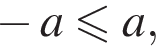 поэтому для отрицательных a неравенство не определено ни при каком x, а при
поэтому для отрицательных a неравенство не определено ни при каком x, а при ![]() неравенство определено при
неравенство определено при ![]() и обращается в
и обращается в  что неверно.
что неверно.
Если же ![]() возведем неравенство в квадрат. Получаем:
возведем неравенство в квадрат. Получаем:
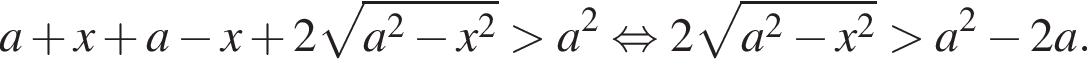
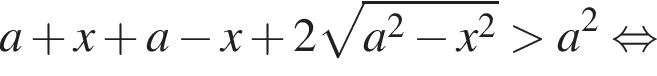
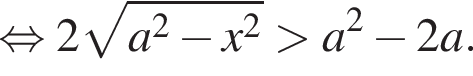
Если 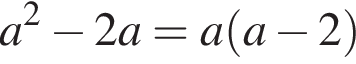 отрицательно, что происходит при
отрицательно, что происходит при 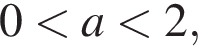 то левая часть неравенства положительна, а правая отрицательна, неравенство выполнено при всех допустимых x.
то левая часть неравенства положительна, а правая отрицательна, неравенство выполнено при всех допустимых x.
Если же ![]() то
то 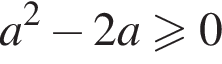 и можно возвести неравенство в квадрат еще раз. Получаем:
и можно возвести неравенство в квадрат еще раз. Получаем:
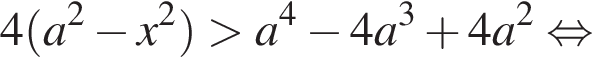
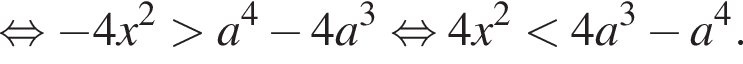
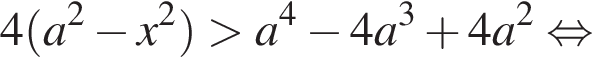
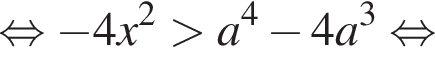
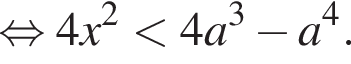
Если 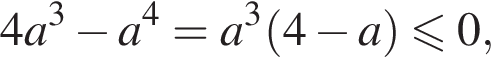 что происходит при
что происходит при ![]() то правая часть отрицательна, а левая неотрицательна, поэтому неравенство не может выполняться.
то правая часть отрицательна, а левая неотрицательна, поэтому неравенство не может выполняться.
Наконец, при 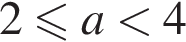 получается условие
получается условие  то есть
то есть
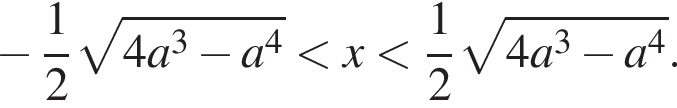
Кроме того, как мы знаем, 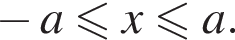 Докажем, что
Докажем, что 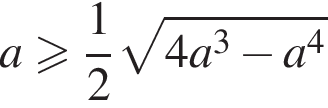 при
при 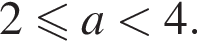 Имеем:
Имеем:
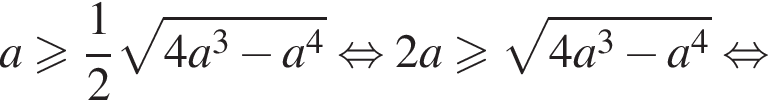
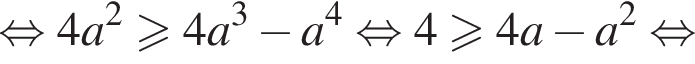
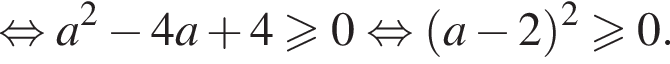
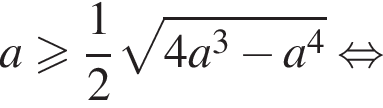

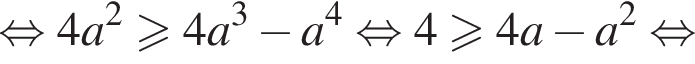
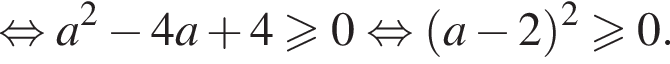
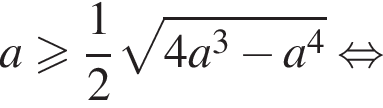

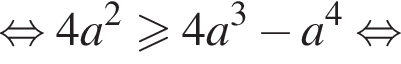
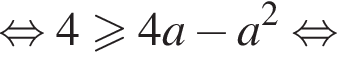
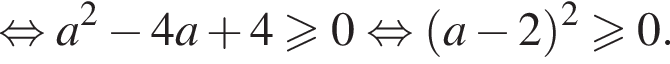
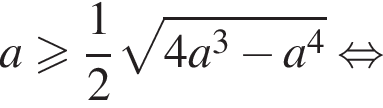

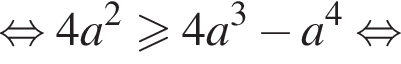
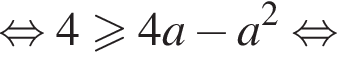
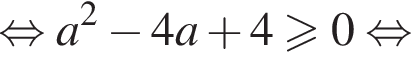
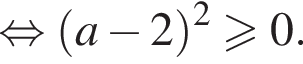
Получаем, что 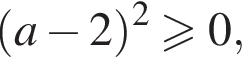 что верно (возведение в квадрат и деление на a2 были допустимы, все числа были положительны). Итак, условие
что верно (возведение в квадрат и деление на a2 были допустимы, все числа были положительны). Итак, условие  будет выполнено автоматически, если выполнено условие
будет выполнено автоматически, если выполнено условие
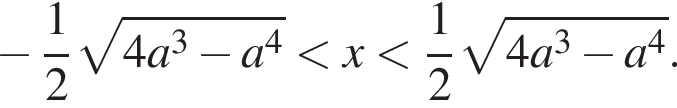
Ответ:
— при  нет решений;
нет решений;
— при 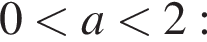
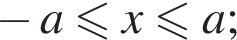
— при 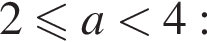
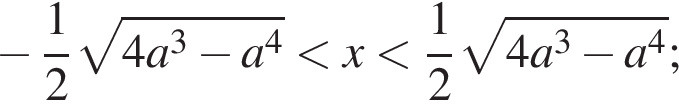
— при  нет решений.
нет решений.
— при  нет решений;
нет решений;
— при 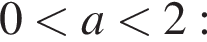
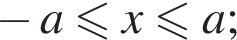
— при 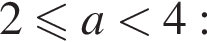
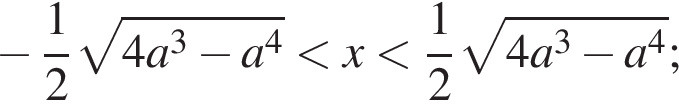
— при  нет решений.
нет решений.
— при  нет решений;
нет решений;
— при 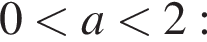
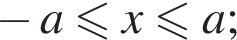
— при 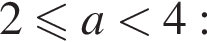
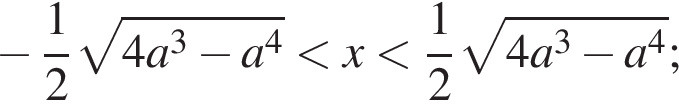
— при  нет решений.
нет решений.
