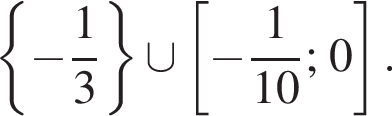Задана система уравнений
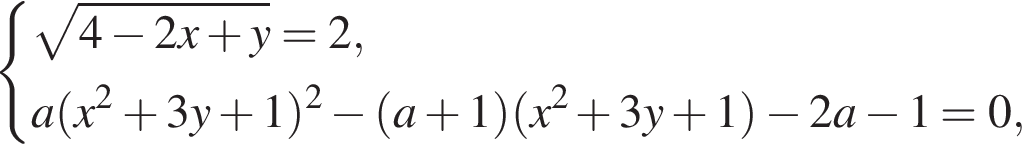
1. Решите систему уравнений при ![]()
2. Найдите все значения параметра a, при каждом из которых система уравнений имеет не более трех решений.
Решение. Возводим первое уравнение в квадрат, находим, что y = 2x, подставим найденное значение во второе уравнение, получим
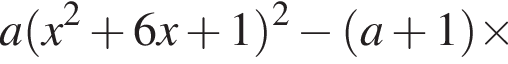
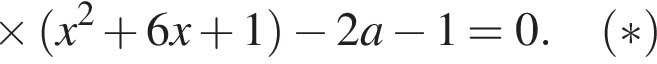
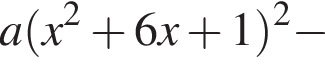
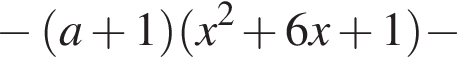
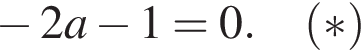

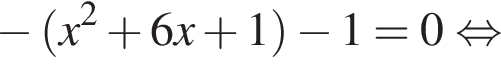
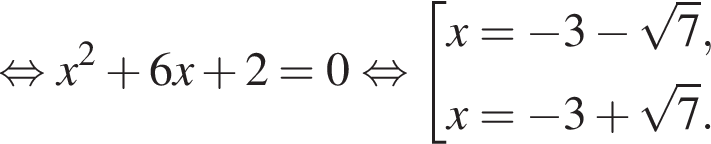
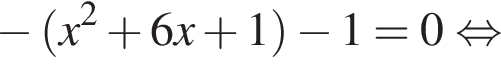
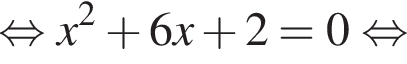
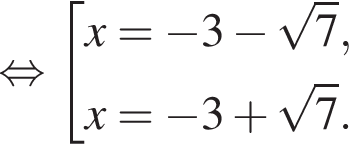
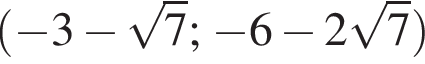 и
и 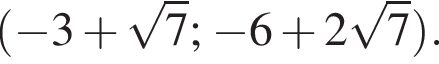
Вернемся ко второму пункту. Поскольку уравнение y = 2x устанавливает взаимно однозначное соответствие между переменными, количество решений системы равно количеству корней уравнения (⁎).
Пусть 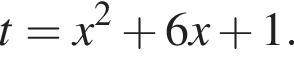 Заметим, что
Заметим, что
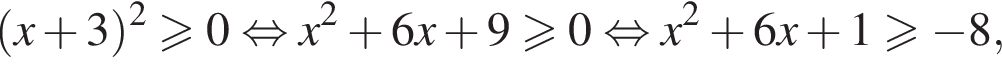
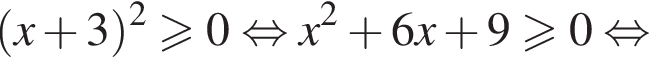
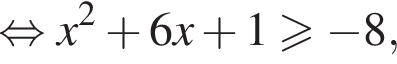
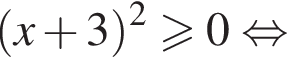
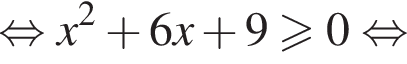
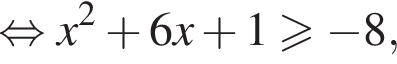
 Каждому значению
Каждому значению  соответствуют два значения переменной x, а значению
соответствуют два значения переменной x, а значению 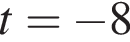 — одно значение переменной x. Тогда уравнение (⁎) записывается в виде
— одно значение переменной x. Тогда уравнение (⁎) записывается в виде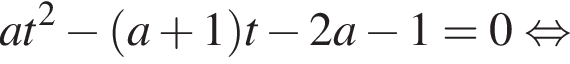
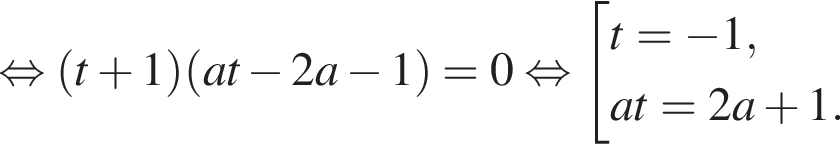
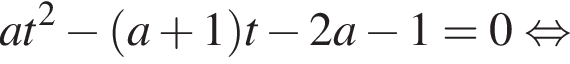
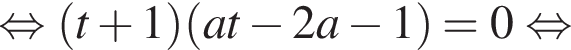
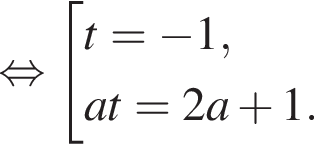
Условие задачи будет выполнено, если будет выполнено одно из условий:
— второе уравнение совокупности не имеет решений;
— корни обоих уравнений совокупности равны;
— корень второго уравнения совокупности не больше −8.
При ![]() уравнение
уравнение 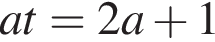 не имеет решений. Если
не имеет решений. Если ![]() то
то
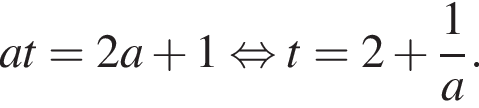
Корни уравнений совокупности совпадают, если
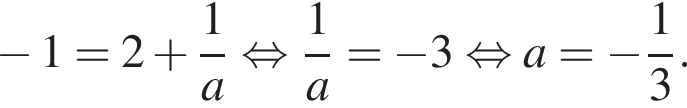
Корень второго уравнения совокупности не больше −8, если
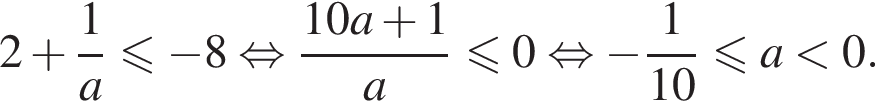
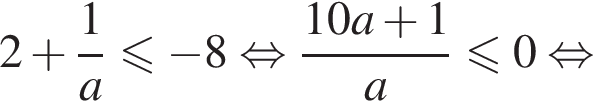
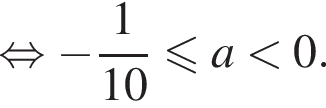
Объединяя все случаи, получаем, что исходная система уравнений имеет не более трех решений при 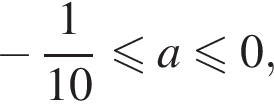 или при
или при 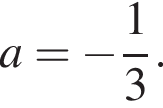
Ответ:
1) 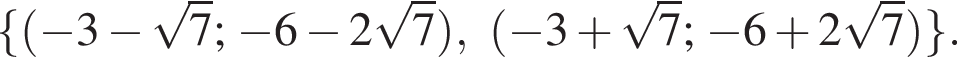
2) 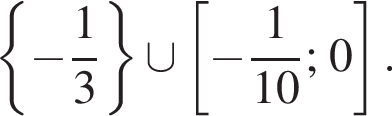
1) 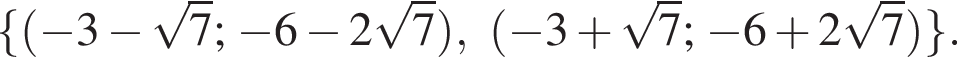
2) 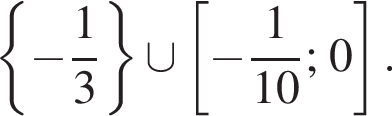
1) 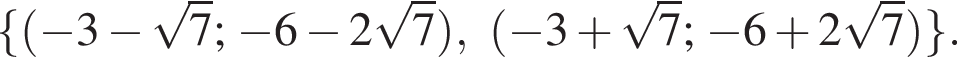
2)