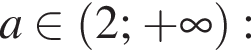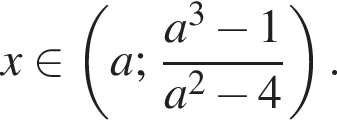Розв’яжіть нерівність 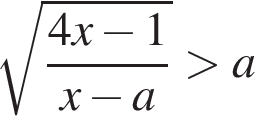 залежно від значень параметра а.
залежно від значень параметра а.
Решение. Разберем несколько случаев. Прежде всего, при ![]() выполняется условие
выполняется условие 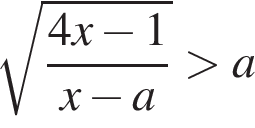 при всех x, при которых определена левая часть, просто потому, что левая часть неотрицательна, а правая отрицательна. Определена же она при
при всех x, при которых определена левая часть, просто потому, что левая часть неотрицательна, а правая отрицательна. Определена же она при 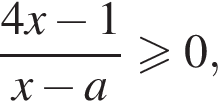 то есть при x, принадлежащих промежутку
то есть при x, принадлежащих промежутку 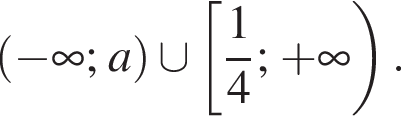 Ясно, что
Ясно, что 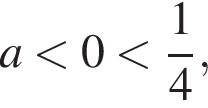 поэтому порядок точек именно такой. Если же
поэтому порядок точек именно такой. Если же ![]() то можно возвести неравенство в квадрат. Получим
то можно возвести неравенство в квадрат. Получим
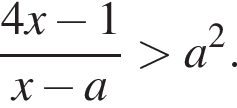
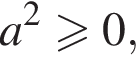 для любого решения этого неравенства левая часть будет положительна, поэтому про условие
для любого решения этого неравенства левая часть будет положительна, поэтому про условие 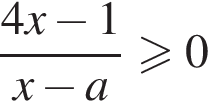 можно больше не думать.
можно больше не думать.Перенесем все в одну часть и решим неравенство методом интервалов:
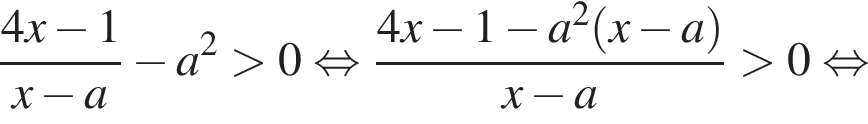
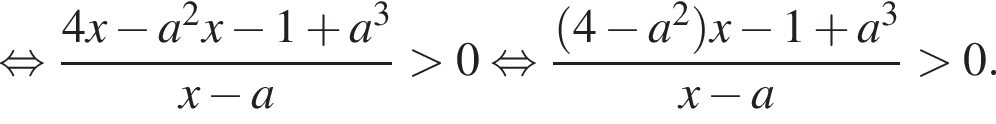
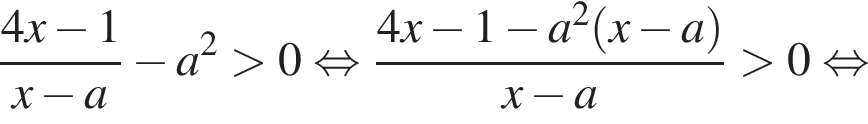
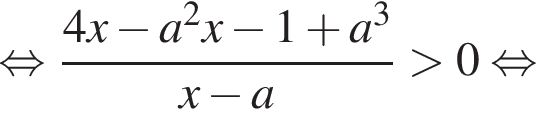
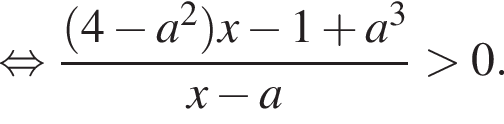
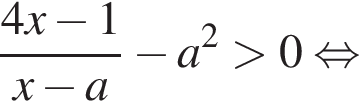
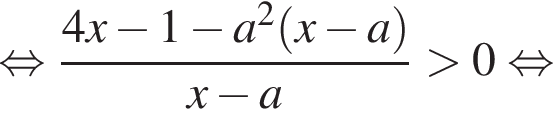
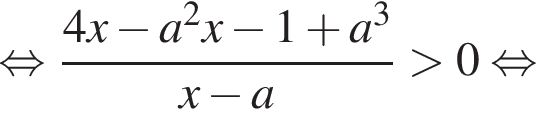
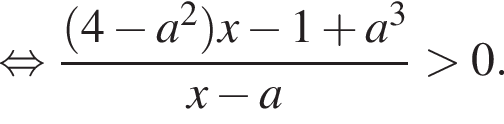
Найдем корень числителя:
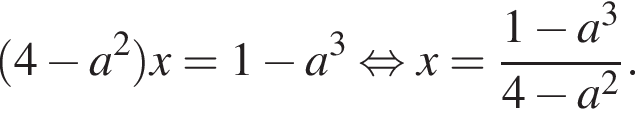
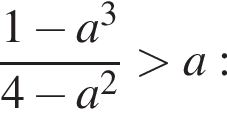
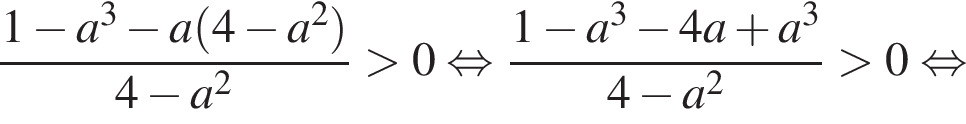
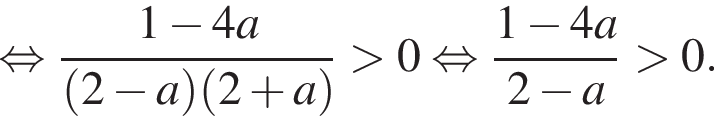
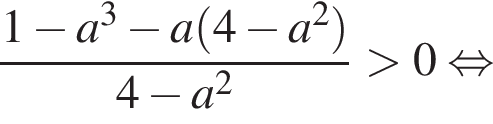
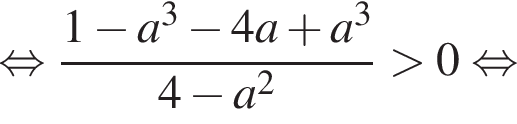
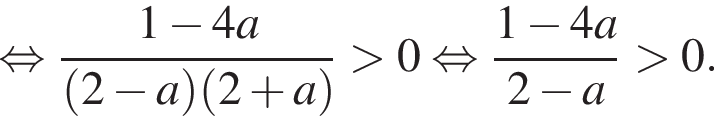
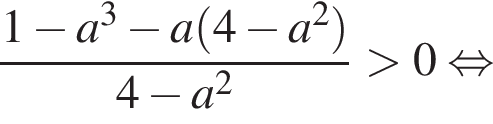
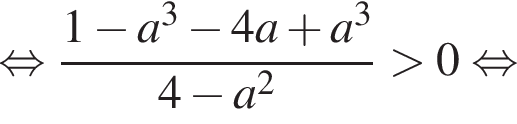
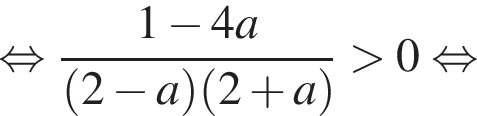
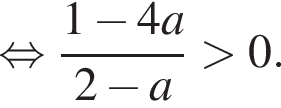
Это верно при 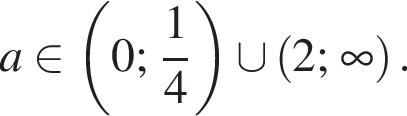 Теперь разберем случаи. При
Теперь разберем случаи. При 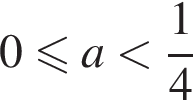 коэффициент при x, равный
коэффициент при x, равный 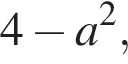 положителен. Значит, множеством решений будет
положителен. Значит, множеством решений будет 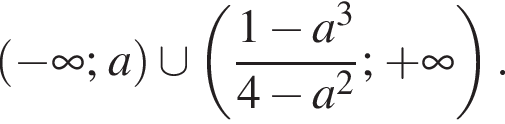
Ответ:
— при
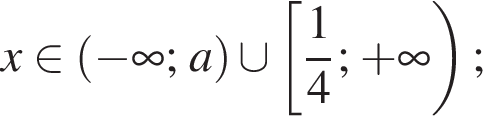
— при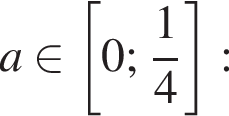
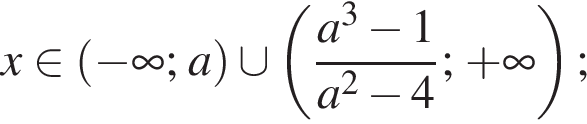
— при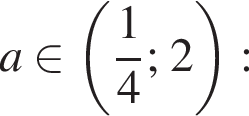
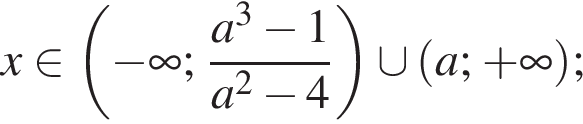
— при 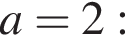
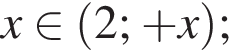
— при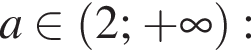
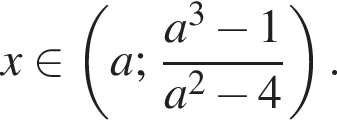
— при
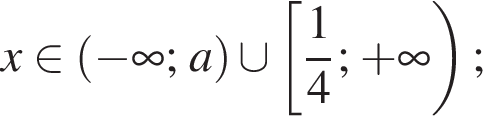
— при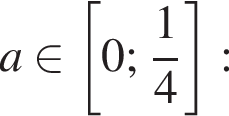
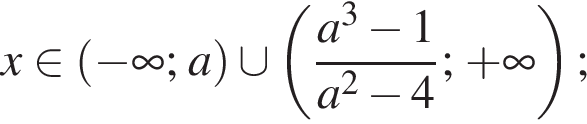
— при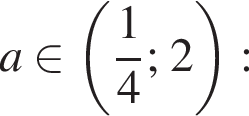
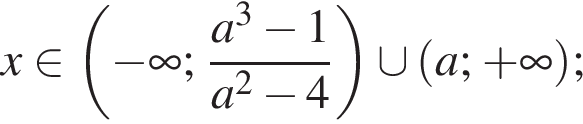
— при 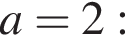
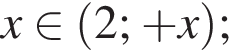
— при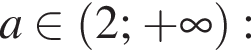
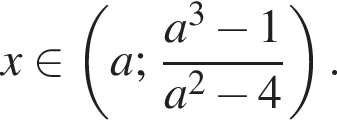
— при
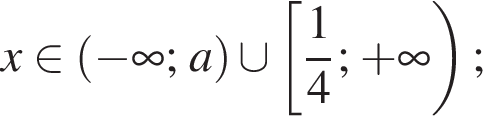
— при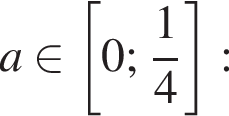
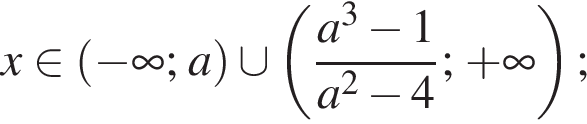
— при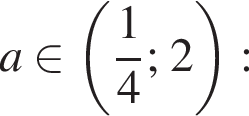
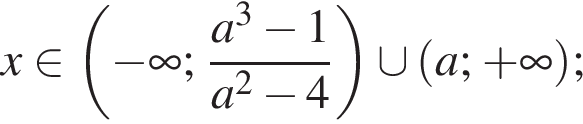
— при 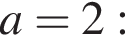
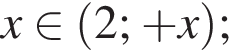
— при