Градусна міра зовнішнього кута A рівнобедреного трикутника ABC
 становить 125°. Знайдіть градусну міру внутрішнього кута B.
становить 125°. Знайдіть градусну міру внутрішнього кута B.
Точка М — середина сторони квадрата ABCD. Площа зафарбованої частини 7 см2, дорівнює 7 см. Знайдіть площу всього квадрата.
У трикутнику ABC
 та
та  Із вершин цих кутів проведено висоти, що перетинаються в точці O. Визначте величину кута AOB.
Із вершин цих кутів проведено висоти, що перетинаються в точці O. Визначте величину кута AOB.
Сторони трикутника, одна з яких на 8 см більша за другу, утворюють кут 120°, а довжина третьої сторони дорівнює 28 см. Знайдіть периметр трикутника.
У трикутнику ABC:
 BD — бісектриса кута B (див. рисунок). Знайдіть градусну міру кута BCA, якщо
BD — бісектриса кута B (див. рисунок). Знайдіть градусну міру кута BCA, якщо 
У сонячний день довжина тіні від дерева становить 16 м. У той самий час тінь від хлопчика, який має зріст 1,5 м, дорівнюе 2 м (див. рисунок). Визначте висоту дерева.
Гострий кут паралелограма дорівнює 60°, а його сторони — 3 см и 4 см. Обчисліть довжину меншої діагоналі паралелограма.
На рисунку зображено вектор
![]() Який із наведених векторів дорівнює вектору
Який із наведених векторів дорівнює вектору ![]()
Сума градусних мір двох кутів паралелограма дорівнює 150°. Знайдіть градусну міру більшого кута паралелограма.
До кола проведено дотичну AB (B — точка дотику) та січну AC, що проходить через центр O кола (див. рисунок). Знайдіть градусну міру кута COB, якщо
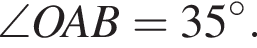
На папері у клітинку зображено трикутник ABC, вершини якого збігаються 3 вершинами клітинок (див. рисунок). Знайдіть площу трикутника ABC, якщо кожна клітинка є квадратом зі стороною завдовжки 1 см.
На рисунку зображено прямокутник ABCD і рівносторонній трикутник ABK, периметри яких відповідно дорівнюють 20 см і 12 см. Знайдіть периметр п'ятикутника AKBCD.
На рисунку зображено ромб ABCD. Знайдіть градусну міру кута ABC, якщо

у прямокутній системі координат зображено прямокутний рівнобедрений трикутник ABC, в якому A (−3; 5) і B (4; 5) (див. рисунок). Знайдіть координати точки C.
До кола з центром у точці О проведено дотичну АВ (В — точка дотику), ВС — хорда, що утворює з радіусом кола кут 35° (див. рисунок). Знайдіть градусну міру кута АВС.
На папері у клітинку зображено паралелограм ABCD, вершини якого збігаються з вершинами клітинок (див. рисунок). Знайдіть площу паралелограма ABCD, якщо кожна клітинка є квадратом зі стороною завдовжки 1 см.
На рисунку зображено квадрат ABCD і трикутник BKC, периметри яких відповідно дорівнюють 24 см і 20 см. Знайдіть периметр п'ятикутника ABKCD.
Діагоналі трапеції ABCD 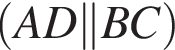 перетинаються в точці O. Знайдіть довжину основи BC трапеції, якщо
перетинаються в точці O. Знайдіть довжину основи BC трапеції, якщо 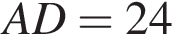 см,
см, см,
см, см.
см.
Бічна сторона рівнобедреного трикутника дорівнює 10 см, а висота, опущена на неї, — 8 см. Знайдіть довжину основи трикутника.
Точки А і В належать колу радіуса 10 см і ділять його на дві дуги, довжини яких відносяться як 3 : 2. Знайдіть довжину більшої дуги кола.
Які з наведених тверджень правильні?
І. Якщо коло має з площиною дві спільні точки, то всі точки кола належать цій площині.
II. Якщо три вершини паралелограма належать площині, то всі точки паралелограма належать цій площині.
III. Якщо круг і площина мають три спільні точки, то всі точки круга належать цій площині.
Прямі, що містять сторони правильного п'ятикутника ABCDF, перетинаються у точках K, L, M, N, P. Знайдіть градусну міру кута AKB.
Знайдіть координати вектора ![]() якщо
якщо 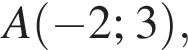
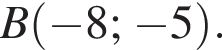
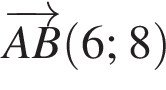
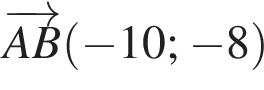
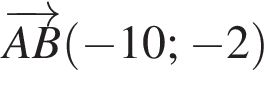
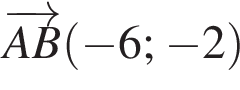
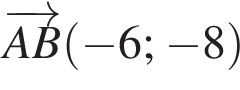
Довжина кола дорівнюе 16π см. Знайдіть площу круга, обмеженого цим колом.
Точки A, B, C i D лежать на колі. Пряма BD — діаметр цього кола (див. рисунок). Знайдіть величину кута ACD, якщо
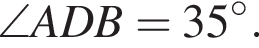
Бісектриса гострого кута A паралелограма ABCD ділить сторону BC на відрізки
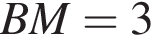 см
см см
см
У трикутнику ABC:  см,
см,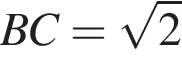 см,
см,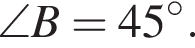 Обчисліть довжину медіани, проведеної з вершини C.
Обчисліть довжину медіани, проведеної з вершини C.
Доберіть таке закінчення речення, щоб утворилося правильне твердження: «Сума квадратів катетів прямокутного трикутника дорівнює...».
Знайдіть градусну міру внутрішнього кута правильного десятикутника.
Обчисліть площу чотирикутника ABCD (див. рисунок), сторони АВ і CD якого паралельні вісі Oy.
На рисунку зображено коло з центром у точці O і рівносторонній трикутник AOB, що перетинає коло в точках M і N. Точка D належить колу. Знайдіть градусну міру кута MDN.
У прямокутник ABCD вписано три круги одного й того самого радіуса (див. рисунок). Визначте довжину сторони BC, якщо загальна площа кругів дорівнює 3π.
У трикутнику ABC: 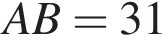 см,
см, см,
см,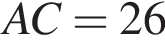 см.
см. см.
см.
На рисунку зображено вектори
![]() і
і ![]() Який із наведених векторів дорівнює вектору
Який із наведених векторів дорівнює вектору ![]()
Чотирикутник ABCD описаний навколо кола. Маючи  см,
см, см,
см,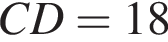 см.
см.
Господарю потрібно зорати город, що має форму прямокутної трапеції. Розміри городу вказано на рисунку. Оранка трактором ділянки площею 100 м2 коштує 8 грн. Скільки грошей (у грн) повинен заплатити господар трактористу за оранку всього городу?
Два кола з центрами в точках O і O1 мають внутрішній дотик (див. рисунок). Обчисліть відстань OO1, якщо радіуси кіл дорівнюють 12 см і 8 см.
Пряма с перетинає паралельні прямі a і b (див. рисунок). Які з наведених тверджень є правильними для кутів 1, 2, 3?
I. ![]() i
i ![]() —
—
II. 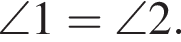
III. 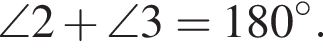
При якому значенні x вектори ![]() і
і 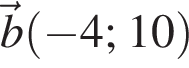 перпендикулярні?
перпендикулярні?
На рисунку зображено паралелограм ABCD, площа якого дорівнюе 60 см2. Точка M належить стороні BC. Визначте площу фігури, що складається з двох зафарбованих трикутників.
У прямокутнику ABCD: 
 Через точки M і K, що належать сторонам AB і BC відповідно, проведено пряму, паралельну AC. Знайдіть довжину більшої сторони трикутника MBK, якщо
Через точки M і K, що належать сторонам AB і BC відповідно, проведено пряму, паралельну AC. Знайдіть довжину більшої сторони трикутника MBK, якщо 
На рисунку зображено коло 3 центром в точці O, довжина якого дорівнює 64 см. Визначте довжину меншої дуги AB кола, якщо
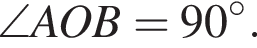
При якому значенні y вектори 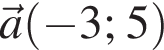 і
і 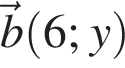 колінеарні?
колінеарні?
Укажіть хибне твердження.
На рисунку зображено рівнобічну трапецію, бічна сторона якої дорівнює
![]() а більша основа — 8. Визначте довжину діагоналі цієї трапеції, якщо ії гострий кут дорівнює 30°.
а більша основа — 8. Визначте довжину діагоналі цієї трапеції, якщо ії гострий кут дорівнює 30°.
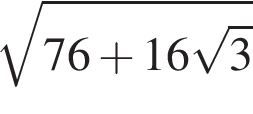
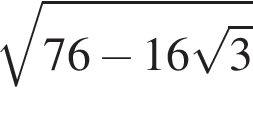
На рисунку зображено ромб, площа якого дорівнює 96 см2. У ромб вписано коло. Визначте площу зафарбованої фігури.
Три прямі, що розміщені в одній площині, перетинаються в одній точці (див. рисунок). Визначте градусну міру кута α.
У трикутнику ABC:
 BD — бісектриса кута B (див. рисунок). Знайдіть градусну міру кута BCA, якщо
BD — бісектриса кута B (див. рисунок). Знайдіть градусну міру кута BCA, якщо 
Які твердження є правильними?
I. Протилежні кути ромба рівні.
II. Діагоналі ромба взаємно перпендикулярні.
III. У будь-який ромб можна вписати коло.
На рисунку зображено квадрат ABCD. Укажіть правильну векторну рівність.
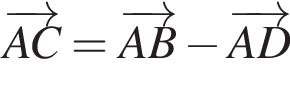
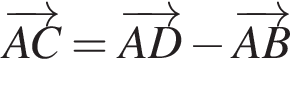
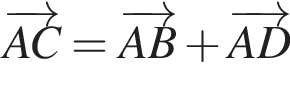
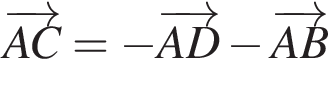
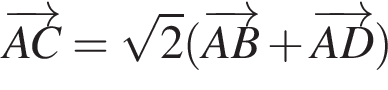
На папері в клітинку зображено трикутник ABC (див. рисунок). Вважайте, що кожна клітинка — квадрат зі стороною завдовжки 1 см. Знайдіть площу трикутника ABC.
На рисунку зображено ескіз емблеми фірми N. Емблема має форму кола, всередині якого розміщено 3 однакових півкола. Один кінець кожного півкола збігається з центром кола, інший кінець лежить на колі. Виготовлення емблеми (усіх її елементів), радіус якої дорівнює 2 м, потребує використання гнучкого матеріалу вартістю 100 грн за 1 м довжини. Укажіть серед наведених найменшу суму грошей, якої вистачить на придбання цього матеріалу для виготовлення емблеми. Вважайте, що місця з'єднання емблеми, позначені на рисунку точками, не потребують додаткових витрат.
Менша сторона прямокутника дорівнює 16 м і утворює з його діагоналлю кут 60°. Середини всіх сторін прямокутника послідовно сполучено. Знайдіть площу утвореного чотирикутника.
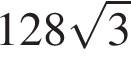 м2
м2 м2
м2У трикутник ABC вписано квадрат KLMN (див. рисунок). Висота цього трикутника, проведена до сторони AC, дорівнює 6 см. Знайдіть периметр квадрата, якщо
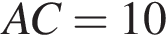 см.
см.
Три промені зі спільним початком лежать в одній площині (див. рисунок). Визначте градусну міру кута γ, якщо
 та
та 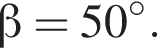
Які з наведених тверджень є правильними?
I. Через дві прямі, що перетинаються, можна провести лише одну площину.
II. Через точку, що не належить площині, можна провести безліч прямих, паралельних цій площині.
III. Якщо дві різні площини паралельні одній і тій самій прямій, то вони паралельні між собою.
У трикутнику ABC задано
 см,
см,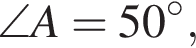
 (див. рисунок). Визначте BC (у см) за теоремою синусів.
(див. рисунок). Визначте BC (у см) за теоремою синусів.
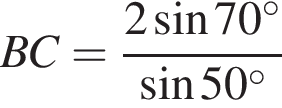
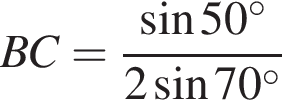

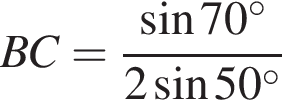
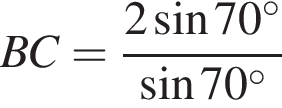
На координатній площині xy зображено коло, центр якого збігається 3 початком координат (див. рисунок). Точки K (8; 6) і M (x; y) належать цьому колу. Визначте координати точки M.
У трикутнику ABC точка
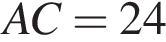 см
см
Точки B і C лежать на прямій, що паралельна прямій а. Скільки існує площин, які паралельні прямій а і проходять через точки В і С?
Пряма n перетинає перпендикулярні прямі l i m (див. рисунок). Визначте градусну міру кута a.
Діагоналі паралелограма ABCD перетинаються в точці O (див. рисунок). Укажіть правильну векторну рівність.
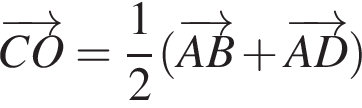
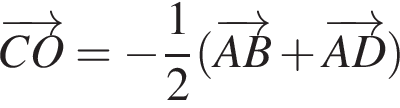
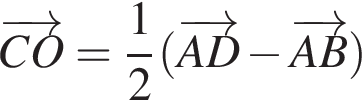
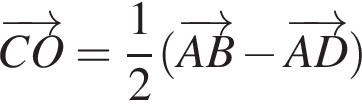
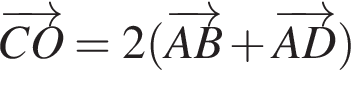
На рисунку зображено рівносторонній трикутник ABC, KM — його середня лінія. Периметр трикутника KBM дорівнює 12 см. Визначте периметр чотирикутника AKMC.
На рисунку зображено круг 3 центром у точці O, радіус якого дорівнюе 12 см. Радіуси OA та OB ділять круг на два кругові сектори. Визначте площу більшого сектора, якщо кут
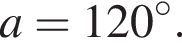
Точка C лежить на осі x прямокутноі системи координат і знаходиться на відстані 5 від точки A (−2; 4). Відрізок AC перетинає вісь y. Знайдіть координати точки C.
У гострокутному трикутнику ABC проведено висоту BM. Визначте довжину сторони AB, якщо  i
i 
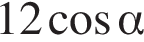

Відрізок AB перетинає площину α в точці O. Проекціі відрізків AO і BO на цю площину дорівнюють 5 см і 20 см відповідно. Знайдіть довжину відрізка AB, якщо  см.
см.
На координатній площині xy зображено коло, яке дотикається до прямих
![]()
![]() та осі x (див. рисунок). Визначте координати точки, яка є центром цього кола.
та осі x (див. рисунок). Визначте координати точки, яка є центром цього кола.
Прямі k, l, m і n лежать в одній площині (див. рисунок). Визначте градусну міру кута α.
Автомобіль рухався по дорозі паралельно паркану NP і зупинився біля закритих воріт KL так, як зображено на рисунку. Відомо, що розмах стулки воріт LM становить 2 м,  м.
м.
У трикутнику ABC проведено висоту BM (див. рисунок). Визначте градусну міру кута MBA, якщо
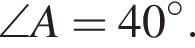
На рисунку зображено паралелограм ABCD, діагоналі якого перетинаються в точціі О. Укажіть пару колінеарних векторів.
