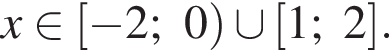Задано неравенство
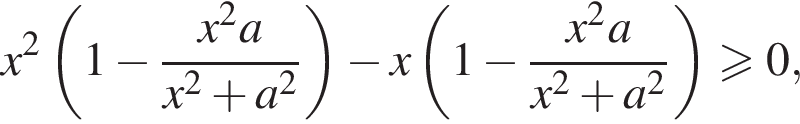
1. Решите неравенство при 
2. При каких значениях 
неравенство выполняется при любых значениях a.
Решение. Домножим неравенство на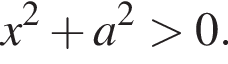 
Получим:
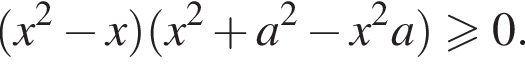
При 
получаем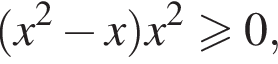 
что верно только при 
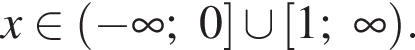При таких x множитель 
неотрицателен, остается лишь выяснить, для каких из этих значений x будет всегда неотрицателен и второй множитель, равный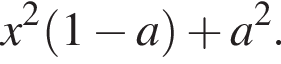 
Ясно, что при 
он всегда неотрицателен, а при 
должно выполняться условие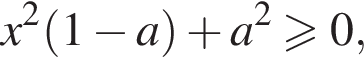 
то есть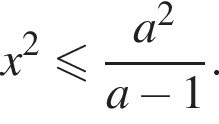 
Найдем наименьшее значение выражения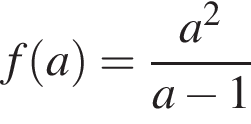 
при 
Имеем:
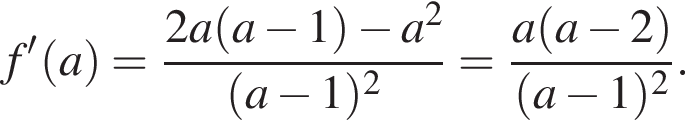
Значит, производная отрицательна при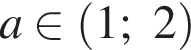 
и положительна при 
Итак, наименьшее значение будет при 
и равно 
Итак, если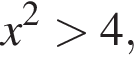 
то можно взять и условие нарушится. А если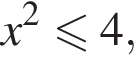 
то вторая скобка будет положительна при любом a. Итак, нужно чтобы 
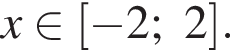Окончательно: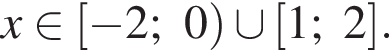 
Ответ:
1) 
2)
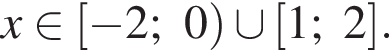
1)
2)
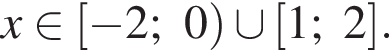
1)
2)